Théorème des résidus
En analyse complexe, le théorème des résidus est un outil puissant pour évaluer des intégrales curvilignes de fonctions holomorphes sur des courbes fermées qui repose sur les résidus de la fonction à intégrer.
Il est utilisé pour calculer des intégrales de fonctions réelles ainsi que la somme de certaines séries. Il généralise le théorème intégral de Cauchy et la formule intégrale de Cauchy.
Énoncé
Soient U un sous-ensemble ouvert et simplement connexe du plan complexe ℂ, {z1, …, zn} un ensemble de n points de U, et f une fonction définie et holomorphe sur U \ {z1, …, zn}.
Si γ est une courbe rectifiable dans U qui ne rencontre aucun des points singuliers zk et dont le point de départ correspond au point d'arrivée (c'est-à-dire un lacet rectifiable), alors :
Ici, Res(f,zk) désigne le résidu de f en zk, et l'indice du lacet γ par rapport à zk. Intuitivement, l'indice du lacet est le nombre de tours autour de zk effectués par un point parcourant tout le lacet. Ce nombre de tours est un entier ; il est positif si γ est parcouru dans le sens inverse des aiguilles d'une montre (sens direct) autour de zk, nul si γ ne se déplace pas du tout autour de zk, et négatif si γ est parcouru dans le sens des aiguilles d'une montre autour de zk.
L'indice est défini par
Exemple
Prenons comme ouvert qui est bien ouvert et simplement connexe et considérons la fonction holomorphe définie par (nous avons donc ici et ).
Calculons alors l'intégrale de cette fonction le long de la courbe définie par (son image étant le cercle unité) avec le théorème des résidus : on a ici et d'où
Variante
« Soit D un ouvert de la sphère de Riemann S2, et soit f une fonction holomorphe dans D sauf peut-être en des points isolés qui sont singuliers pour f. Soit Γ le bord orienté d'un compact A contenu dans D, et supposons que Γ ne contienne aucun point singulier de f, ni le point à l'infini. Les points singuliers zk contenus dans A sont alors en nombre fini, et on a la relation :
où Res(f, zk) désigne le résidu de la fonction f au point zk ; la sommation est étendue à tous les points singuliers zk ∈ A, y compris éventuellement le point à l'infini[1]. »
Application au calcul d'intégrales réelles
Pour évaluer des intégrales réelles, le théorème des résidus s'utilise souvent de la façon suivante : l'intégrande est prolongé en une fonction holomorphe sur un ouvert du plan complexe ; ses résidus sont calculés, et une partie de l'axe réel est étendue à une courbe fermée en lui attachant un demi-cercle dans le demi-plan supérieur ou inférieur. L'intégrale suivant cette courbe peut alors être calculée en utilisant le théorème des résidus. Souvent, grâce au lemme d'estimation ou au lemme de Jordan, la partie de l'intégrale sur le demi-cercle tend vers zéro, quand le rayon de ce dernier tend vers l'infini, laissant seulement la partie de l'intégrale sur l'axe réel, celle qui initialement nous intéressait.
La liste ci-dessous n'est pas exhaustive mais elle permet d'avoir une idée générale de la technique utilisant le théorème des résidus, on aborde :
- les intégrales du « premier type »: où est une fonction rationnelle ;
- les intégrales du « deuxième type » : ;
- les intégrales du « troisième type » : ;
- les intégrales du « quatrième type » : combinaison des deux cas précédents en considérant la valeur principale de Cauchy de l'intégrale.
Premier type
Soit le calcul de l'intégrale réelle suivante :
avec une fonction rationnelle ayant un nombre fini de points singuliers et dont aucun n'appartient au cercle centré à l'origine et de rayon 1. On obtient par le théorème des résidus :
où est définie comme suit :
Deuxième type
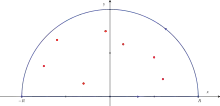
Soit le calcul de l'intégrale impropre suivante :
avec ayant un ensemble de points singuliers isolés purement complexes. Si et si converge, alors
Remarque : dans le cas où est une fonction rationnelle définie par avec et des polynômes, sans racines réelles, il suffit d'exiger que (où représente le degré du polynôme) pour que les hypothèses soient vérifiées, la convergence de l'intégrale étant même absolue.
Troisième type
Soit le calcul de l'intégrale impropre suivante :
avec comportant un ensemble de point singuliers isolés purement complexes. Si et si converge, alors :
et
Quatrième type
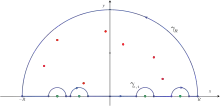
Les intégrales du deuxième et du troisième type s'étendent aux cas avec un nombre fini n de pôles situés sur l'axe réel. Il s'agit alors d'une intégrale impropre et l'on considère alors la valeur principale de Cauchy de l'intégrale.
Soit une fonction holomorphe sur ℂ sauf en un ensemble de pôles simples réels, , et de singularités isolées purement complexes, . Supposons que l'on se trouve dans un des deux cas suivant :
- il existe et tels que pour tout complexe de module supérieur ou égal à ,
ou
- avec et il existe tels que pour tout complexe de module supérieur ou égal à .
Alors la valeur principale de Cauchy (notée ) de l'intégrale existe et on a :
Remarque : on peut aisément étendre la formule au demi-plan inférieur en changeant le signe de la première somme et en considérant uniquement les singularités purement complexe dans ce demi-plan.
Application aux calculs de sommes
Le théorème des résidus permet aussi de calculer certaines sommes infinies. Soit une fonction ayant pour chaque entier un résidu égal au -ième terme général d'une somme infinie ainsi qu'un ensemble de résidus correspondant à d'autres points. Supposons que l'intégrale de cette fonction le long d'un lacet rectifiable infiniment grand soit nulle. On a alors par le théorème des résidus :
Par conséquent, on peut exprimer la somme infinie par une autre somme (en général finie) de résidus :
Les énoncés ci-dessous donnent des exemples plus généraux de cas pour lesquels cette méthode est applicable :
- les sommes du "premier type" : ;
- les sommes du "deuxième type" : .
Premier type
Soit le calcul de la somme suivante :
avec ayant un ensemble de singularités isolées. Supposons que la condition suivante soit respectée :
- il existe et tels que pour tout complexe de module supérieur ou égal à .
Alors, nous avons :
et
Deuxième type
Soit le calcul de la somme suivante :
avec ayant un ensemble de singularités isolées. Supposons que satisfasse à la même condition que pour les sommes du premier type à savoir :
- il existe tels que pour tout complexe de module supérieur ou égal à .
Alors, la somme converge absolument et on a :
Voir aussi
Notes et références
- Henri Cartan, Théorie élémentaire des fonctions analytiques d'une ou plusieurs variables complexes [détail de l’édition], p. 93.
- Murray R. Spiegel (en), Variables complexes, Schaum (ISBN 2-7042-0020-3)
- (en) Serge Lang, Complex Analysis, Springer, 1999 (ISBN 0-387-98592-1)
- (en) Joseph Bak et Donald J. Newman, Complex Analysis, Springer, (ISBN 0-387-94756-6)
- Ernst Lindelöf, Le Calcul des résidus et ses applications à la théorie des fonctions, Paris, Gauthier-Villars,





























![{\displaystyle \gamma :[0,2\pi ]\to \mathbb {C} }](https://img.franco.wiki/i/d306e876bd67e88fe44898816489ecbb580cee2c.svg)















![{\displaystyle \gamma :[0,2\pi ]\to \mathbb {C} ,\gamma (t)\mathrm {e} ^{\mathrm {i} t}.}](https://img.franco.wiki/i/948bb49cedfbb075cd40d5edd39a60a211014a80.svg)


























![[-r,r]](https://img.franco.wiki/i/5dbcf3f99b353b618465500fe9576e0850885ffd.svg)




















































![{\displaystyle \gamma _{\varepsilon ,j}:[0,\pi ]\to \mathbb {C} ,\gamma _{\varepsilon ,j}(t)=x_{j}+\varepsilon \mathrm {e} ^{i(\pi -t)}}](https://img.franco.wiki/i/07290bb6cd9866e30f20bb1bc3f7bebbebe826c6.svg)



















![{\displaystyle \int _{\gamma }g(z)~\mathrm {d} z=2\mathrm {i} \pi \left[S+\sum _{z_{k}\in E}\mathrm {Res} (g;z_{k})\right]=0.}](https://img.franco.wiki/i/5f12b878cf68d37b23a5fdb92fa414c32706b3ff.svg)



















![{\displaystyle \lim _{N\to \infty }\int _{C(0,R)}f(z)\pi \cot(\pi z)~\mathrm {d} z=2\pi \mathrm {i} \lim _{N\to \infty }\left[\sum _{-N,n\notin E}^{N}f(n)+\sum _{z_{k}\in E}\mathrm {Res} \left(f(z)\pi \cot(\pi z);z_{k}\right)\right].}](https://img.franco.wiki/i/72b34c7768ef302cb98350a473edea64b08bd3d0.svg)



























