Vecteur euclidien
En mathématiques, et plus précisément en géométrie euclidienne, un vecteur euclidien[1] est un objet géométrique possédant une direction, un sens et une norme. On l'utilise par exemple en physique et en ingénierie pour modéliser une force.
On parle aussi parfois de vecteur géométrique[2] dans le plan euclidien (deux dimensions) et de vecteur spatial[3] dans l'espace à trois dimensions.
Définitions et exemples
Vecteur, vecteur euclidien
En physique et en ingénierie, on travaille souvent dans l'espace euclidien. Quand on parle de vecteur, on se réfère alors à un vecteur euclidien, c'est-à-dire à une grandeur physique (par exemple une force) caractérisée par :
- une direction (une droite Δ qui n'est pas orientée) ;
- un sens (orientation de la droite Δ, signe de sa mesure algébrique) ;
- une norme (la longueur du vecteur, par exemple l'intensité d'une force).
On parle aussi d'orientation ou de droite orientée pour se référer au couple (direction, sens).
En mathématiques, un vecteur est défini plus généralement comme un élément d'un espace vectoriel. Selon cette définition, les vecteurs sont des entités abstraites pouvant ou non avoir une grandeur et une orientation. Les vecteurs euclidiens sont donc un cas particulier de vecteurs, et il est important en mathématiques de préciser si l'on se réfère à l'un ou à l'autre.
Vecteur lié, vecteur libre
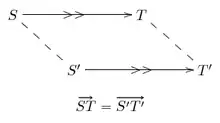
Dans l'espace euclidien, un vecteur lié est un vecteur euclidien possédant un point initial et un point final donnés. Il est lié à ce point initial, et l'on peut déduire le point final du vecteur lié et du point initial.
Toujours dans l'espace euclidien, un vecteur libre désigne une famille de vecteurs liés ayant la même norme, la même direction et le même sens[4]. Un vecteur libre n'est donc pas lié à un point initial donné.
Par exemple, dans la figure ci-contre, les vecteurs liés et sont distincts car ils ont des points initiaux différents. En revanche, les vecteurs libres et sont égaux.
Notation et représentation graphique
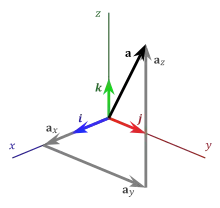
Un vecteur euclidien est généralement représenté graphiquement à l'aide d'un segment de droite et d'une flèche indiquant son sens[5]. La norme du vecteur euclidien correspond alors à la longueur du segment de droite représenté graphiquement, et son orientation est l'angle orienté qu'il forme avec le repère cartésien (0, ).
En tant que variable, il peut être noté de différentes façons. Pour le distinguer des autres types de vecteurs, on place souvent une flèche horizontale gauche-droite au-dessus de la variable le représentant. Alternativement, on peut omettre la flèche et utiliser une lettre majuscule ou minuscule, en italique ou en caractères gras, comme n'importe quel vecteur. Ainsi un vecteur peut-il s'écrire sous la forme , etc.[6].
Par exemple, dans la figure ci-contre, le vecteur euclidien a est représenté par une flèche noire dans un système de coordonnées cartésiennes en 3 dimensions (). On a représenté également les vecteurs unitaires () ainsi que les composantes () du vecteur a.
Opérations
Plusieurs opérations peuvent être définies sur l'ensemble des vecteurs euclidiens : l'addition, la soustraction, la multiplication, le produit scalaire, le produit vectoriel, etc. Les structures algébriques associées à ces opérations ne sont pas développées dans cet article introductif, mais le sont dans des articles plus avancés tels que « Espace euclidien » et « Espace vectoriel ».
Addition de vecteurs
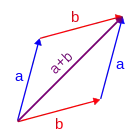
Les vecteurs libres peuvent être additionnés graphiquement en les alignant bout à bout (cf. article relation de Chasles). Ils peuvent également être additionnés analytiquement en additionnant chacune de leurs composantes définies par rapport à un référentiel donné.
Étant donnés quatre points A, B, C, D du plan euclidien, l'addition des deux vecteurs et se construit en définissant un point E tel que (en traçant le parallélogramme BCDE).
Le vecteur somme s'identifie alors au vecteur .
L'addition de vecteurs satisfait toutes les propriétés de l'addition numérique. Son élément neutre est le vecteur nul. L'opposé d'un vecteur est un vecteur de même norme et de même direction, mais de sens opposé.
L'addition de deux vecteurs colinéaires (i.e. ayant la même direction) s'identifie à celle de leurs mesures algébriques.
Dans l'espace, un vecteur peut être défini par ses coordonnées sur les trois axes x, y et z d'un repère cartésien, axes dirigés respectivement par les vecteurs , et . La somme de deux vecteurs euclidiens est alors :
Notes et références
- Jean Salençon, Mécanique des milieux continus, t. 1 : Concepts généraux, Éditions École Polytechnique, , 370 p. (lire en ligne), p. 296.
- Ammar Yahia, « Chapitre 1: Les vecteurs géométriques », sur http://www.civil.usherbrooke.ca, Université de Sherbrooke.
- Interactive Power Electronics Seminar (iPES), « Contrôle de courant basée sur le vecteur spatial pour un onduleur de tension triphasé MLI à six interrupteurs », sur http://www.ipes.ethz.ch, École polytechnique fédérale de Zurich.
- On parle alors de classe d'équivalence.
- (en) Kiyoshi Itō, Encyclopedic Dictionary of Mathematics, MIT Press, , 2e éd., 2148 p. (ISBN 978-0-262-59020-4, lire en ligne), p. 1678.
- Harris Benson (trad. Marc Séguin, Benoît Villeneuve, Bernard Marcheterre et Richard Gagnon), Physique 1 Mécanique, Éditions du Renouveau Pédagogique, , 4e éd., 465 p., p. 22.
Voir aussi
Articles connexes
Bibliographie
Marielle Champagne, Option science Physique La mécanique, Éditions du Renouveau Pédagogique, , 330 p.















