Surface de révolution

Dans un espace affine eucliden de dimension 3, on dit qu'une surface (S) admet une droite (D) comme axe de rotation si elle est globablement invariante par rotation autour de (D). On dit alors que la surface est une surface de révolution d'axe (D)[1]

Pour tout point M de la surface de révolution, le cercle d'axe (D) passant par M est inclus dans (S). Ce cercle est appelé le parallèle de (S) passant par M[1].

Tout plan contenant l'axe de rotation est appelé un plan méridien. L'intersection de la surface de révolution par un plan méridien est une méridienne. L'intersection de la surface (S) par un demi-plan de frontière (D) est une demi-méridienne. Une surface de révolution est entièrement déterminée par son axe de révolution et une demi-méridienne.

Une partie (C) de (S) est appelée directrice de (S) si son intersection avec tout parallèle de (S) est non vide[2]. Une directrice engendre la surface (S) par rotation. Une demi-méridienne est un cas particulier de directrice.

L'exemple le plus simple d'une courbe tracée dans l'espace est celui d'une droite affine ${\displaystyle c:u\mapsto c(0)+u\cdot {\vec {V}}}$ où l'on peut supposer ${\displaystyle {\vec {V}}}$ unitaire. On suppose cette droite distincte de l'axe (Oz).

• Si ${\displaystyle {\vec {V}}}$ est orthogonal à ${\displaystyle {\vec {z}}}$, la surface obtenue est le plan passant par c(0) et parallèle au plan (xOy).
• Si ${\displaystyle {\vec {V}}}$ est colinéaire à ${\displaystyle {\vec {z}}}$, la surface obtenue est un cylindre de révolution d'axe Oz.
• Si ${\displaystyle {\vec {V}}}$ n'est ni orthogonal ni colinéaire à ${\displaystyle {\vec {z}}}$, mais que ${\displaystyle {\overrightarrow {Oc(0)}}}$, ${\displaystyle {\vec {V}}}$ et ${\displaystyle {\vec {z}}}$ sont des vecteurs coplanaires, alors la surface engendrée est un cône de révolution d'axe ${\displaystyle {\vec {z}}}$ et de demi-angle au sommet ${\displaystyle \arccos({\vec {V}},{\vec {z}})}$.
• Dans les autres cas, la surface obtenue est une surface réglée non dégénérée, à savoir un hyperboloïde d'axe de révolution ${\displaystyle {\vec {z}}}$. La méridienne de cette surface est une hyperbole

La sphère de centre 0 et de rayon R est la surface obtenue par rotation autour de l'axe (Oz) d'un cercle de centre O et de rayon R tracé dans un plan vertical.

Le tore est la surface obtenue par rotation d'une méridienne constituée d'un cercle dont le centre n'appartient pas à l'axe de rotation. Le tore est aussi engendré par deux cercles non situés dans un plan méridien, les cercles de Villarceau.

• Surfaces de révolution avec leurs méridiennes et leurs parallèles
• 
  Cylindr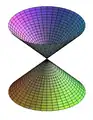e.
• 
  Cône.
• 
  Sphère.
• 
  Tore

Pièces d'échec

Dans la vie de tous les jours aussi, beaucoup d'objets de fabrication humaine présentent des surfaces de révolution. La raison étant que la symétrie de révolution en facilite la fabrication ou l'usage. Parfois, il ne s'agit que d'une simple recherche artistique, une volonté de « perfection ».

• Les bifaces sont les premiers outils montrant cette recherche d'une plus grande maniabilité.
• Un grand nombre de stylos sont des surfaces de révolution (mais les formes varient d'une marque à l'autre).
• Les verres de consommation, quelle que soit leurs formes, sont souvent, en première approximation, des surfaces de révolution.
• Les quilles de bowling ou de jonglage
• Dans le style Staunton, parmi les pièces d'échec, les pions sont les seules pièces qui soient des surfaces de révolution (en premier plan à droite sur l'illustration). Cependant, le pied de toutes les pièces est une surface de révolution.
  • Etc.

Les méridiennes possèdent pour axe de symétrie l'axe de rotation de la surface de révolution. Ce sont des géodésiques de cette surface[3], mais la surface peut contenir d'autres géodésiques.

Pour tout point M de la surface de révolution, l'intersection de la surface avec un plan perpendiculaire à l'axe et passant par M contient le parallèle passant par M. Pour tout point M de (S) non situé sur l'axe de rotation, la tangente en M au cercle parallèle est toujours perpendiculaire au plan méridien passant par M[4]. En particulier, la tangente en M au cercle parallèle est perpendiculaire à la tangente en M à la méridienne.

Si le point M est régulier, le plan tangent en M à la surface est perpendiculaire au plan méridien[4] et contient la tangente au cercle parallèle et la tangente à la courbe méridienne. La normale à la surface rencontre l'axe de rotation en un point indépendant de la position de M sur son cercle parallèle. La surface conique engendrée par la normale est alors dite normale à la surface de révolution[5].

Un ensemble de révolution possédant deux axes de révolution coplanaires et distincts est une réunion de sphères concentriques[1].

Le théorème de Guldin permet de lier l'aire d'une portion de surface de révolution à la longueur de la portion de méridienne qui l'engendre.

Une surface de révolution d'axe (Oz) est une surface qui admet une équation cartésienne de la forme[6] ${\displaystyle f\left({\sqrt {x^{2}+y^{2}}},z\right)=0}$ où ${\displaystyle f}$ est une fonction de classe ${\displaystyle C^{1}}$ sur un ouvert de ${\displaystyle \mathbb {R} ^{2}}$ à valeurs dans ${\displaystyle \mathbb {R} }$.

Remarque: la condition «de classe ${\displaystyle C^{1}}$» est imposée ici pour avoir une certaine régularité. Tauvel, par exemple[7], parle d'«ensemble de révolution» et n'impose pas de condition sur f.

Plus généralement, on reconnait que (S) est une surface de révolution s'il existe une fonction ${\displaystyle f}$ de classe ${\displaystyle C^{1}}$ sur un ouvert de ${\displaystyle \mathbb {R} ^{2}}$ à valeurs dans ${\displaystyle \mathbb {R} }$, une application affine φ non constante de ${\displaystyle \mathbb {R} ^{3}}$ dans ${\displaystyle \mathbb {R} }$ et un point I tels que l'équation de (S) soit[8]: ${\displaystyle f\left(IM^{2},\varphi (M)\right)=0}$ L'axe de rotation est alors la droite orthogonale au plan ${\displaystyle \varphi (M)=0}$ passant par I.

Exemple : la surface d'équation

${\displaystyle x^{2}+2y^{2}+5z^{2}+4yz+2x+6y=0}$

est une surface de révolution car l'équation peut encore s'écrire:

${\displaystyle \left[(x+1)^{2}+(y+3)^{2}+z^{2}\right]+(y+2z)^{2}-10=0}$

qui est de la forme

${\displaystyle IM^{2}+[\varphi (M)]^{2}-10=0}$

Son axe de rotation est la droite passant par ${\displaystyle I(-1,-3,0)}$ et de direction ${\displaystyle {\vec {u}}(0,1,2)}$.

Si on note h_M la distance orientée de M au plan ${\displaystyle \varphi (M)=0}$ et r_M la distance de M à l'axe de rotation, l'équation devient

${\displaystyle (h_{M}-h_{I})^{2}+r_{M}^{2}+5h_{M}^{2}-10=0}$

qui est l'équation d'un ellipsoïde de révolution.

Il est possible de déterminer l'équation d'une surface engendrée par une directrice ${\displaystyle ({\mathcal {C}})}$ paramétrée, tournant autour d'un axe passant par I et de direction ${\displaystyle {\vec {u}}}$ en éliminant le paramètre dans le système[9] ${\displaystyle {\begin{cases}IM^{2}=IN^{2}\\{\overrightarrow {MN}}.{\vec {u}}=0.\end{cases}}}$ où M est un point de (S), N un point de ${\displaystyle ({\mathcal {C}})}$ et «.» le produit scalaire

Soit une courbe tracée dans ℝ³ de paramétrage ${\displaystyle (x(u),y(u),z(u))}$, généralement de classe ${\displaystyle {\mathcal {C}}^{2}}$. La rotation d'axe (Oz) engendre une surface paramétrée :

${\displaystyle X(u,\theta )={\begin{pmatrix}\cos(\theta )&-\sin(\theta )&0\\\sin(\theta )&\cos(\theta )&0\\0&0&1\end{pmatrix}}{\begin{pmatrix}x(u)\\y(u)\\z(u)\end{pmatrix}}={\begin{pmatrix}x(u)\cos(\theta )-y(u)\sin(\theta )\\x(u)\sin(\theta )+y(u)\cos(\theta )\\z(u)\end{pmatrix}}.}$

On peut prendre pour u l'abscisse curviligne s de la courbe, ce qui simplifie certains calculs.

La surface étant également engendrée par la rotation d'une méridienne, on peut supposer y(u) = 0. On désigne alors généralement par r(u) la quantité x(u). Le triplet ${\displaystyle (r(u),\theta ,z(u))}$ représente les coordonnées cylindriques d'un point quelconque de la surface.

Un hyperboloïde

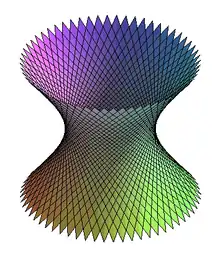
• l'hyperboloïde est obtenu par rotation d'une droite non coplanaire avec l'axe (Oz). Prenons comme point d'origine de la droite le point appartenant à sa perpendiculaire commune avec (Oz) (perpendiculaire qu'on peut supposer être (Ox)) et supposons pour simplifier qu'il soit à une distance 1 de l'axe (Oz) :

${\displaystyle {\vec {c(0)}}=(1,0,0)}$ et ${\displaystyle {\vec {V}}=(0,a,b)}$ où ${\displaystyle a^{2}+b^{2}=1}$.

Un paramétrage admissible de la droite est : ${\displaystyle {\vec {OM(u)}}={\vec {Oc(0)}}+u{\vec {V}}}$.

Un paramétrage de la surface engendrée par la rotation de la droite autour de l'axe (Oz) est : ${\displaystyle {\vec {OM(u,\theta )}}={\begin{pmatrix}\cos(\theta )-au\sin(\theta )\\\sin(\theta )+au\cos(\theta )\\bu\end{pmatrix}}}$

On peut vérifier que la surface a pour équation : ${\displaystyle {\frac {x^{2}+y^{2}}{a^{2}}}-{\frac {z^{2}}{b^{2}}}={\frac {1}{a^{2}}}}$.

• La sphère de centre 0 et de rayon R est la surface obtenue par rotation autour de l'axe (Oz) d'un cercle de centre O et de rayon R tracé dans un plan vertical. Un paramétrage de la sphère est :

${\displaystyle X(u,\theta )={\begin{pmatrix}R\cos(u)\cos(\theta )\\R\cos(u)\sin(\theta )\\R\sin(u)\end{pmatrix}}}$

qui est une variante des coordonnées sphériques.

• Le tore est la surface obtenue par rotation d'une méridienne constituée d'un cercle dont le centre n'appartient pas à (Oz). Un paramétrage du tore est :

  ${\displaystyle X(u,\theta )={\begin{pmatrix}\left(R+r\cos(u)\right)\cos(\theta )\\\left(R+r\cos(u)\right)\sin(\theta )\\r\sin(u)\end{pmatrix}}}$

où donc ${\displaystyle r<R}$

• 

  Trompette de Gabriel
  La trompette de Gabriel est obtenue par rotation d'une portion d'hyperbole autour de son asymptote. Un paramétrage de la trompette est :

${\displaystyle X(u,\theta )={\begin{pmatrix}u\cos(\theta )\\u\sin(\theta )\\{\dfrac {1}{u}}\end{pmatrix}}}$

où ${\displaystyle u\in ]0,1]}$.

On dispose des formules générales suivantes[10] :

Propriété métrique	Résultat
Première forme fondamentale	${\displaystyle \mathrm {I} =(r'^{2}+z'^{2})\mathrm {d} u^{2}+r^{2}\mathrm {d} \theta ^{2}}$
Seconde forme fondamentale	${\displaystyle \mathrm {II} ={\frac {z''r'-r''z'}{\sqrt {r'^{2}+z'^{2}}}}\mathrm {d} u^{2}+{\frac {z'r}{\sqrt {r'^{2}+z'^{2}}}}\mathrm {d} \theta ^{2}}$
Forme d'aire	${\displaystyle \omega =r{\sqrt {r'^{2}+z'^{2}}}\mathrm {d} u\wedge \mathrm {d} \theta }$
Courbures principales	${\displaystyle {\frac {z''r'-r''z'}{(r'^{2}+z'^{2})^{3/2}}}}$ et ${\displaystyle {\frac {z'}{r{\sqrt {r'^{2}+z'^{2}}}}}}$
Courbure de Gauss	${\displaystyle \mathrm {K} ={\frac {z'(r'z''-z'r'')}{r(r'^{2}+z'^{2})^{2}}}}$

Dans le cas où u représente l'abscisse curviligne s de la méridienne, on a :

${\displaystyle r'^{2}+z'^{2}=1}$

${\displaystyle r'r''+z'z''=0}$

${\displaystyle z'(r'z''-z'r'')=-r'^{2}r''-z'^{2}r''=-r''}$

et les formules se simplifient en :

Propriété métrique	Résultat
Première forme fondamentale	${\displaystyle \mathrm {I} =\mathrm {d} s^{2}+r^{2}\,\mathrm {d} \theta ^{2}}$
Seconde forme fondamentale	${\displaystyle \mathrm {II} =(z''r'-r''z')\,\mathrm {d} s^{2}+z'r\,\mathrm {d} \theta ^{2}}$
Forme d'aire	${\displaystyle \omega =r\,\mathrm {d} s\wedge \mathrm {d} \theta }$
Courbures principales	${\displaystyle z''r'-r''z'=-{\frac {r''}{z'}}}$ et ${\displaystyle {\frac {z'}{r}}}$
Courbure de Gauss	${\displaystyle \mathrm {K} =-{\frac {r''}{r}}}$

En utilisant les résultats précédents, on donne ci-dessous les courbures d'un certain nombre de surfaces de révolution:

Courbe	Paramétrage (r(u),z(u))	Courbure de Gauss
sphère de rayon 1	${\displaystyle (\cos(u),\sin(u))}$	1
tore	${\displaystyle (R+r\cos(u)),r\sin(u))}$	${\displaystyle {\frac {\cos(u)}{r(R+r\cos(u))}}}$
pseudosphère	${\displaystyle (u-\tanh(u),{\frac {1}{\cosh(u)}})}$	${\displaystyle -1}$
ellipsoïde de révolution	${\displaystyle (a\cos(u),c\sin(u))}$	${\displaystyle {\frac {c^{2}}{(a^{2}\sin ^{2}(u)+c^{2}\cos ^{2}(u))^{2}}}}$
hyperboloïde de révolution à une nappe	${\displaystyle (a\cosh(u),c\sinh(u))}$	${\displaystyle -{\frac {c^{2}}{(a^{2}\sinh ^{2}(u)+c^{2}\cosh ^{2}(u))^{2}}}}$
hyperboloïde de révolution à deux nappes	${\displaystyle (a\sinh(u),\pm c\cosh(u))}$	${\displaystyle {\frac {c^{2}}{(a^{2}\cosh ^{2}(u)+c^{2}\sinh ^{2}(u))^{2}}}}$
caténoïde	${\displaystyle (\cosh(u),u}$)	${\displaystyle -{\frac {1}{\cosh(u)^{4}}}}$