Surface réglée
En géométrie, une surface réglée est une surface par chaque point de laquelle passe une droite, appelée génératrice, contenue dans la surface.
Représentation paramétrique
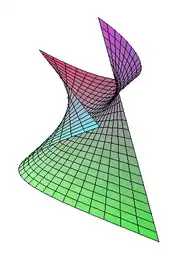
On peut décrire une surface réglée S en la considérant comme la réunion d'une famille de droites D(u) dépendant d'un paramètre u parcourant une partie I de l'ensemble des réels. Il suffit pour cela de se donner pour chaque u dans I un point P(u) et un vecteur directeur de D(u). On obtient alors une représentation paramétrique de la surface S :
L'arc paramétré par est appelé une courbe directrice de S[1].
Dans l'exemple ci-contre, on a pris
Exemples
Outre le plan qui est une surface réglée évidente, les surfaces réglées les plus connues sont :
- le cône, dont toutes les génératrices ont un point commun, appelé sommet du cône ;
- le cylindre, dont les génératrices sont parallèles ;
- le paraboloïde hyperbolique, qui possède deux familles de génératrices ;
- l'hyperboloïde à une nappe, qui possède également deux familles de génératrices ;
- l'hélicoïde, seule surface minimale réglée, avec le plan ;
- le ruban de Möbius, surface réglée non orientable ;
- le conoïde, dont les génératrices sont parallèles à un plan donné (plan directeur) et passent par une droite (axe du conoïde).
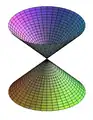 Cône.
Cône. Cylindre.
Cylindre.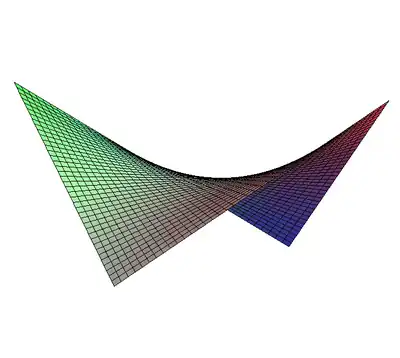 Paraboloïde hyperbolique.
Paraboloïde hyperbolique.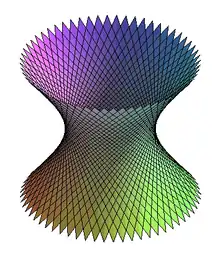 Hyperboloïde à une nappe.
Hyperboloïde à une nappe.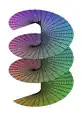 Hélicoïde.
Hélicoïde.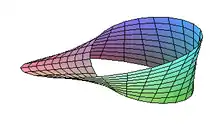 Ruban de Möbius.
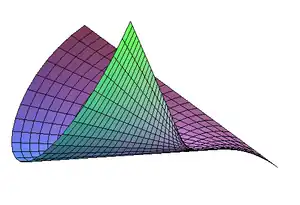
Ruban de Möbius.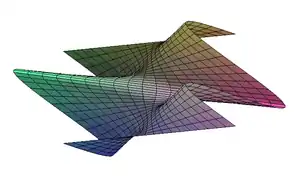 Conoïde.
Conoïde.
Plan tangent
En tout point régulier d'une surface réglée, le plan tangent contient la génératrice qui passe par ce point[1].
En effet, la représentation paramétrique donne une base du plan tangent en M(u, v), constituée des vecteurs ce dernier vecteur dirigeant la génératrice D(u).
Notamment, si par un point passent deux génératrices distinctes, celles-ci y engendrent le plan tangent. C'est notamment le cas des surfaces doublement réglées, comme l'hyperboloïde à une nappe ou le paraboloïde hyperbolique[2].
Si, pour toute valeur de u dans I, en deux points quelconques de la génératrice D(u) les plans tangents sont confondus, on dit que la surface est développable.
On obtient un tel exemple de surface développable en prenant la réunion des tangentes à une courbe gauche, ou autrement dit une développable des tangentes, qui est alors courbe directrice de la surface réglée obtenue[1]. Plus généralement, toute surface développable est constituée de parties de cônes, de cylindres, et de développable des tangentes à une courbe, qui se recollent le long d'une génératrice avec un même plan tangent[2].
Applications
Chaudronnerie industrielle

La chaudronnerie est le travail des métaux en feuilles (tôles). La mise en forme des tôles utilise essentiellement deux techniques : le roulage (ou cintrage) et le pliage.
Le roulage donne des surfaces de révolution, portions de cônes ou de cylindres. Ce sont donc des surfaces réglées.
Le pliage permet d'approcher des surfaces réglées par des polyèdres, les plis/arêtes correspondant à des génératrices de la surface que l'on veut approcher.
Les parties grises de la photo ci-jointe sont des surfaces réglées d'une pièce chaudronnée.
Articles connexes
- Surface réglée standard, qui contient une classification en géométrie algébrique.
- Géométrie différentielle des surfaces, où l'on trouvera des formules permettant de calculer la courbure.
Références
- Jacqueline Lelong-Ferrand et Jean-Marie Arnaudiès, Cours de mathématiques : Géométrie et cinématique, t. 3, Paris, Dunod Université, , 2e éd. (1re éd. 1975), 733 p. (ISBN 978-2-04-003080-3), chap. 8 (« Propriétés affines des surfaces »), p. 462-467.
- Paulette Libermann, « Géométrie différentielle classique : Algèbre, analyse, géométrie », dans Dictionnaire des mathématiques, Algèbre, analyse, géométrie, Albin Michel & Encyclopædia Universalis, , 924 p. (ISBN 978-2-226-09423-0), p. 508.
Liens externes
(en) Eric W. Weisstein, « Ruled Surface », sur MathWorld




