Surface développable
Une surface développable est une surface réglée telle que le plan tangent est le même le long d'une génératrice. On peut donc « faire rouler sans glisser » une telle surface sur un plan, le contact se faisant le long d’une droite, comme pour un cylindre ou un cône.
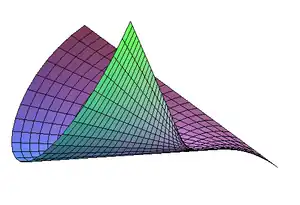
Caractérisations
On peut caractériser les surfaces développables par différentes définitions :
- une surface développable est une surface réglée dont toute génératrice est stationnaire, c'est-à-dire telle que le plan tangent à la surface est le même en tout point de la génératrice.
- une surface développable est une surface réglée dont les génératrices possèdent une enveloppe (éventuellement réduite à un point (cas des cônes), voire un point à l'infini (cas des cylindres).
- la courbure de Gauss d'une surface développable est nulle (elle ne l'est pas pour une surface réglée quelconque).
Les surfaces développables sont des surfaces applicables sur le plan, et réciproquement, toute surface applicable sur le plan de classe est incluse dans une surface développable. Lorsqu'on applique la surface sur le plan, on dit qu'on la « développe ».
Exemples
- les cônes
- les cylindres,
- l’hélicoïde développable dont l'arête de rebroussement est une hélice circulaire, résultant de la torsion d'un cercle,
- le ruban de Möbius
- On obtient une surface développable en prenant la surface réglée engendrée par les tangentes à une courbe gauche : il s'agit d'une développable des tangentes.
- Considérons une surface S et une ligne de courbure (C) de S. Alors la surface réglée engendrée par les vecteurs normaux à S en tout point de (C) est une surface développable[1].
Applications
D'un point de vue pratique, une forme correspondant à une surface développable est facilement construite à partir d'un patron plan tracé selon sa « développée » sur un matériau plan et souple : tôle, carton, plastique, etc. Cette caractéristique est utilisée aussi bien dans les fabrications de tôlerie ou dans la construction navale que dans la réalisation des maquettes en carton.
Voir aussi
Articles connexes
Liens externes
- Mathieu Perriollat, Paramétrisation et reconstruction des surfaces développables à partir d’images (thèse de doctorat (Vision pour la robotique)), , 138 p. (lire en ligne), chap. 3 (« Surfaces développables »), p. 15-25
Références
- Henri Cartan, Cours de calcul différentiel, Hermann, 1967, rééd. 1977, p. 340
