Géométrie hyperbolique

Un triangle hyperbolique sans cercle circonscrit (les trois médiatrices sont parallèles).

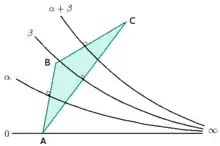
Les propriétés du plan qu'on peut démontrer à partir des axiomes d'Euclide (ou d'une formulation plus rigoureuse et moderne, telle que celle de Hilbert), à l'exception de l'axiome des parallèles, sont dites appartenir à la géométrie absolue. Ainsi, par exemple, on montre que deux perpendiculaires à une même droite n'ont pas de points communs[note 17], et donc qu'il existe toujours des parallèles (c'est pourquoi la géométrie elliptique n'est pas une géométrie absolue). De nombreuses propriétés de la géométrie hyperbolique coïncident de même avec celles de la géométrie euclidienne, parfois au prix d'une reformulation : ainsi, on démontre aisément que les bissectrices intérieures d'un triangle quelconque sont concourantes (la démonstration classique n'utilise pas la notion de parallèles), et donc qu'il existe un cercle inscrit dans ce triangle ; les propriétés des médiatrices amèneraient à penser qu'elles sont également concourantes et donc qu'il existe également un cercle circonscrit, mais ce résultat est faux en général dans le plan hyperbolique, car deux perpendiculaires à deux droites concourantes peuvent être parallèles ; ce qui reste vrai, c'est que si deux médiatrices d'un triangle se coupent, les trois médiatrices sont concourantes (le même résultat est également vrai pour les hauteurs du triangle)[note 18].

Droites passant par P et asymptotes à la droite R ; l'angle θ est l'angle de parallélisme.

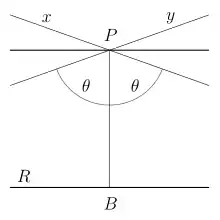
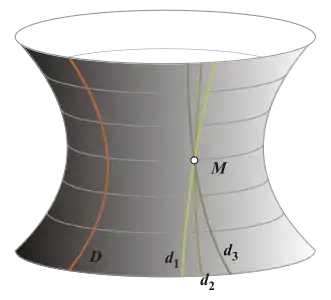
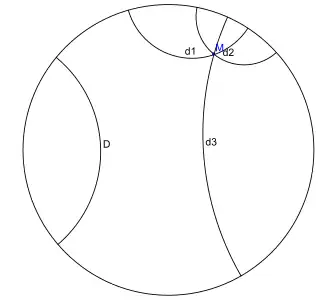
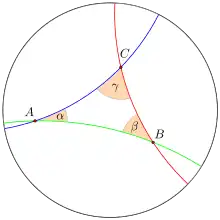
On obtient la géométrie hyperbolique à partir de la géométrie absolue en remplaçant l'axiome des parallèles (ou plus exactement la version qu'en a donné Proclus[note 3]) par un axiome affirmant par exemple que « il existe au moins deux droites concourantes parallèles à une même troisième ». On démontre alors que pour toute droite D et pour tout point P non sur D, il existe une infinité de droites passant par P et ne rencontrant pas D, situées entre deux droites limites formant un angle 2θ ne dépendant que de la distance de P à D ; θ est appelé angle de parallélisme (le calcul de cet angle en fonction de la distance sera fait dans la section consacré aux propriétés métriques)[24]. Les deux droites limites sont dites parallèles asymptotes à D (certains auteurs réservent le terme de parallèles aux parallèles asymptotes ; les autres droites non sécantes sont alors dites ultraparallèles, ou parfois hyperparallèles). On démontre[note 19] que si deux droites du plan sont non sécantes (parallèles au sens euclidien usuel), ou bien elles sont asymptotes, ou bien il existe une et une seule droite perpendiculaire aux deux ; le segment découpé sur cette perpendiculaire commune correspond alors à la distance minimale entre ces deux droites (laquelle est nulle pour deux droites asymptotes). Les notions euclidiennes de direction d'une droite, définie comme relation d'équivalence entre droites parallèles, et de point à l'infini d'une droite (défini, en géométrie projective, comme l'intersection de cette droite avec la droite de l'infini) disparaissent, mais il reste possible de définir une relation d'équivalence entre parallèles asymptotes (les droites possédant désormais deux directions) ainsi qu'une notion de points à l'infini ; par exemple, dans le modèle du disque de Poincaré, les points à l'infini forment un cercle limitant le disque et chaque droite (représentée dans ce modèle par un arc de cercle) coupe ce cercle limite en deux points correspondant à ses deux directions, deux droites étant parallèles asymptotes si elles ont un point à l'infini en commun[25].

Un horocycle (en bleu) dans le modèle du disque de Poincaré et des normales, convergeant asymptotiquement vers un point à l'infini.

Représentation d'un apeirogone régulier inscrit dans un horocycle, dans le modèle du disque de Poincaré.

Pavage du disque de Poincaré par des pentagones réguliers.

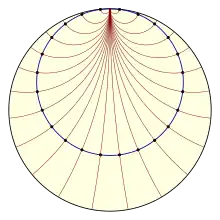
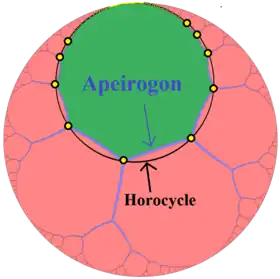
Les propriétés métriques d'un cercle de rayon r diffèrent de celles du plan euclidien : son périmètre et son aire sont respectivement supérieurs à 2πr et à πr². Mais de plus, certaines propriétés caractéristiques des droites euclidiennes définissent des courbes du plan hyperbolique qui n'ont pas d'analogue euclidien, mais qui par certains côtés peuvent s'interpréter comme des cercles généralisés : les points situés à une distance fixe d d'une droite donnée D forment une courbe appelée un hypercycle ; les courbes dont les normales en tout point forment une famille de droites asymptotiquement parallèles sont appelées des horocycles (ou parfois horicycles[20]). Dans le modèle du disque de Poincaré, les cercles, les horocycles et les hypercycles (ainsi que les droites) sont tous représentés par des cercles ou des arcs de cercle. Par trois points formant un triangle passe une courbe unique de cette famille (un cercle, un horocycle ou un hypercycle), qui généralise donc la notion de cercle circonscrit à ce triangle. Enfin, si une suite de points P_n (${\displaystyle n\in \mathbb {Z} }$) est telle que les segments S_n = [P_nP_n+1] sont tous de même longueur et que les angles entre ces segments sont tous égaux et suffisamment grands[note 20], elle forme un polygone régulier infini, appelé un apeirogone régulier, inscrit dans un horocycle ou dans un hypercycle[26].

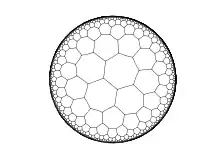
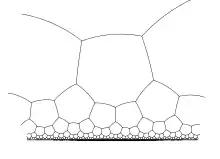
L’angle au sommet d’un polygone régulier à n côtés (qui vaut n–2/nπ dans le plan euclidien) dépend de la longueur a du côté en géométrie hyperbolique et peut être rendu aussi petit que l’on veut[note 21] ; c’est pourquoi on peut paver de manière uniforme le plan hyperbolique avec des polygones réguliers d'un nombre quelconque de côtés, et avec n'importe quel nombre de polygones ayant un sommet commun[27] (alors qu'il n'existe dans le plan euclidien que trois pavages réguliers). L'exemple ci-contre représente (dans le modèle du disque de Poincaré) un pavage par des pentagones réguliers ayant cinq angles droits.

Contrairement au plan euclidien, il existe une échelle absolue des longueurs dans le plan hyperbolique, analogue au rayon de la sphère en géométrie sphérique, et qu'on peut interpréter comme une « courbure », une déformation du plan euclidien rendant par exemple la somme des angles d'un triangle inférieure à 180° ; Gauss a défini, plus généralement, une notion de courbure intrinsèque pour une surface quelconque, en n'utilisant que des lignes tracées sur la surface ; avec cette définition, on démontre que le plan hyperbolique est une surface de courbure constante négative K[28]. En choisissant convenablement l'unité de longueur, on peut prendre K égal à –1 ; c'est cette convention qui sera utilisée dans la suite. Pour des formules plus générales, il faudrait multiplier par –K toutes les longueurs y apparaissant ; ainsi, dans le cas général, la relation entre les côtés d’un triangle rectangle devient cosh(Kc) = cosh(Ka) cosh(Kb), et l'aire d'un disque de rayon r est ${\textstyle 2\pi {\frac {\cosh Kr-1}{K^{2}}}}$.

Si P est un point hors de la droite D et H son projeté orthogonal sur D (avec a = HD la distance de P à D), les formules données ci-dessous pour un triangle rectangle PHM, avec M sur D s'éloignant à l'infini, aboutissent à la formule donnant le sinus de l'angle de parallélisme θ, formule découverte par Lobatchevski[29] :

${\displaystyle \sin \theta ={\frac {1}{\cosh a}}={\frac {2}{\mathrm {e} ^{a}+\mathrm {e} ^{-a}}}}$.

Cet angle tend très rapidement vers 0 lorsque P s'éloigne de D, c'est-à-dire que la plupart des droites passant par P sont parallèles à D[24].

Triangle hyperbolique (représenté dans le disque de Poincaré).

Le périmètre d'un cercle de rayon r est 2π sinh(r) = π(e^r – e^–r) et l'aire du disque correspondant est 2π(cosh(r) – 1) ; ainsi, l'aire d'un disque croît beaucoup plus vite avec son rayon que dans le plan euclidien[30]. Il en va tout autrement de l'aire Δ d'un triangle (dont les angles α, β et γ sont d'autant plus petits que les côtés sont grands) : Lambert a démontré que Δ = π – (α + β + γ), formule identique au signe près à la formule de Girard en trigonométrie sphérique, et qui montre au passage que la somme des angles d'un triangle est toujours inférieure à π[31].

Formellement, on peut obtenir les résultats correspondant au plan hyperbolique en supposant le triangle tracé sur une sphère de rayon imaginaire R = i (c'est-à-dire que R² = –1)[note 22] ; en d'autres termes, en remplaçant dans les formules classiques de la trigonométrie sphérique les sinus et les cosinus des arcs (et non ceux des angles) par les sinus et cosinus hyperboliques (et en corrigeant certains signes). Ainsi, pour un triangle ABC, avec les mêmes conventions que dans le cas sphérique (côtés notés a = BC, b = AC et c = AB ; angles correspondants notés α, β et γ), on a une loi des cosinus : cosh(c) = cosh(a) cosh(b) – sinh(a) sinh(b) cos(γ), une loi des cosinus duale : cos(γ) = – cos(α) cos(β) + sin(α) sin(β) cosh(c), et une loi des sinus : ${\textstyle {\frac {\sin \alpha }{\sinh a}}={\frac {\sin \beta }{\sinh b}}={\frac {\sin \gamma }{\sinh c}}}$[32]. En particulier, pour un triangle rectangle en C, on a cosh(c) = cosh(a) cosh(b) ; comme cosh(x) ≈ 1 + x²/2 pour x suffisamment petit, on retrouve à la limite le théorème de Pythagore[33].

Trois triangles idéaux dans le modèle du disque de Poincaré.

Une autre figure n'ayant pas d'analogue euclidien est obtenue en éloignant indéfiniment les sommets d'un triangle ordinaire : on obtient à la limite trois parallèles asymptotes deux à deux, les sommets étant rejetés à l'infini. Tous les triangles obtenus ainsi, appelés triangles idéaux, sont isométriques, et, ayant leurs trois angles nuls, ont (d'après la formule de Lambert) une aire égale à π, la plus grande possible pour un triangle[34].

On appelle déplacement du plan une isométrie qui conserve l'orientation. Les rotations du plan hyperbolique sont définies exactement comme en géométrie euclidienne : si r est la rotation de centre C et d'angle α, l'image de A par r, A' = r(A) est le point tel que CA' = CA et que l'angle ${\textstyle {\widehat {ACA'}}=\alpha }$ ; la démonstration de ce que cette transformation est bien un déplacement ne dépend pas de l'axiome des parallèles. En revanche, il n'existe pas de vrais analogues des translations en géométrie hyperbolique ; ce qui s'en rapproche le plus est une rotation autour d'un point à l'infini C, transformation formée du composé de deux symétries orthogonales ayant pour axes deux droites concourantes en ce point (donc parallèles asymptotes) ; dans les itérations d'une telle transformation, chaque point parcourt les sommets d'un apeirogone régulier inscrit dans un horocycle de centre C (cette transformation est parfois appelée une horolation de centre C). Plus généralement, on démontre que tout déplacement du plan hyperbolique est composé de deux symétries orthogonales : c’est l'identité si les axes de symétrie sont confondus, c’est une rotation ordinaire s'ils se coupent, c’est une horolation s'ils sont parallèles asymptotes, et enfin, si les deux axes de symétrie sont ultraparallèles, ce déplacement est une translation le long de leur perpendiculaire commune, les autres points parcourant des hypercycles ayant pour axe cette perpendiculaire[35].

Représentation en coordonnées axiales de cercles autour de l'origine ; le contour en rouge représente le plan hyperbolique H tout entier.

L'invention par René Descartes des systèmes de coordonnées qui portent son nom a donné naissance à la géométrie analytique, permettant de résoudre des questions de géométrie à l'aide des méthodes de l'algèbre[36] - [37]. Il est possible de repérer de même les points du plan hyperbolique par des couples de nombres, le système le plus usité étant celui des coordonnées axiales (prenant pour coordonnées d'un point ses projections orthogonales sur deux axes perpendiculaires)[38], mais ces systèmes sont loin d'être aussi commodes, en raison de la complexité des formules décrivant les figures usuelles (droites et cercles) ou permettant de calculer angles et distances ; c'est pourquoi la plupart des applications informatiques passent plutôt par des calculs dans le modèle du disque de Poincaré[note 23].

Parallèles et hyperparallèles dans le modèle de Klein-Beltrami.

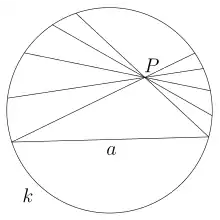
Dans ce modèle, l'espace hyperbolique est une boule ouverte euclidienne. En dimension 2, le plan hyperbolique est donc modélisé par un disque ouvert. Les droites de l'espace hyperbolique sont des segments dont les extrémités appartiennent au bord de la boule ; la distance est donné par la métrique de Cayley-Klein. La représentation des droites hyperboliques est aisée dans ce modèle, mais les angles ne sont pas conservés et les cercles sont représentés par des ellipses.

La sphère (ou le cercle en dimension 2) limitant le domaine du modèle correspond à des points de l'espace hyperbolique situés à l'infini. Aussi, plus on s'approche du bord du domaine et plus les distances ont l'air de se contracter dans le modèle.

Pavage du plan hyperbolique par des heptagones réguliers, dans le modèle du disque de Poincaré.

Comme dans le modèle de Klein-Beltrami, l'espace hyperbolique est représenté dans ce modèle par une boule ouverte euclidienne (et donc par un disque en dimension 2), mais les droites de cet espace hyperbolique sont des arcs de cercles perpendiculaires au bord de la boule ; la distance est définie par la métrique de Poincaré. L'intérêt de cette représentation est que, localement, la métrique de l'espace est, à un facteur près, la métrique euclidienne du modèle. En particulier, l'angle entre deux droites de l'espace hyperbolique est égal à l'angle de la géométrie euclidienne formé par les deux arcs de cercles du modèle représentant ces deux droites. On dit que la représentation de l'espace hyperbolique est conforme.

Comme dans le modèle de Klein-Beltrami, la sphère (ou le cercle en dimension 2) limitant le domaine du modèle correspond à des points de l'espace hyperbolique situés à l'infini, les distances semblant se contracter lorsqu'on s'approche du bord du domaine.

Pavage du plan hyperbolique par des heptagones réguliers, dans le modèle du demi-plan de Poincaré.

Dans ce modèle, l'espace hyperbolique est un demi-espace ouvert de ${\displaystyle \mathbb {R} ^{n}}$. En dimension 2, le plan hyperbolique est donc modélisé par un demi-plan euclidien. Les droites de cet espace hyperbolique sont des arcs de cercles perpendiculaires à l'hyperplan (ou à la droite en dimension 2) limitant le demi-espace ; la distance est définie à l'aide de la métrique ${\textstyle \mathrm {d} s^{2}={\frac {\mathrm {d} x^{2}+\mathrm {d} y^{2}}{y^{2}}}.}$ La représentation est là aussi conforme.

Dans ce modèle, l'hyperplan (ou la droite en dimension 2) limitant le domaine correspond à des points de l'espace hyperbolique situés à l'infini. Les distances se contractent en s'approchant de cet hyperplan, et se dilatent en s'en éloignant.

Dans ce modèle, étudié par Poincaré et surtout par Killing dans les années 1880[41], l'espace hyperbolique est une nappe d'un hyperboloïde muni d'une métrique particulière. Plus précisément, dans l'espace de Minkowski, c'est-à-dire Rⁿ⁺¹, muni de la pseudo-métrique –dx2
0 + dx2
1 + ... + dx2
n, c'est la nappe de l'hyperboloïde d'équation x2
0 – x2
1 – ... – x2
n = 1 telle que x₀ > 0, munie de la pseudo-métrique induite, qui est en fait une métrique riemannienne homogène. Minkowski a montré en 1908 que ce modèle s'identifiait à l'espace des vecteurs-vitesse (Geschwindigkeitsvectoren) de la relativité restreinte[42].

Surfaces de révolution de courbure de Gauss constante.

La pseudosphère (ou tractricoïde) utilisée par Beltrami comme modèle du plan hyperbolique.

Eugenio Beltrami a proposé en 1868 de prendre une surface de courbure constante négative comme modèle du plan hyperbolique (et d'appeler « droites » les géodésiques de cette surface)[43] - [note 11]. Il est impossible (d'après un théorème de Hilbert) d'obtenir ainsi un modèle du plan hyperbolique tout entier qui ne présente pas de singularités, mais la pseudosphère en est la meilleure représentation ; elle présente de plus l'avantage de conserver la métrique usuelle, en mesurant les distances le long des géodésiques. Henri Poincaré a démontré plus généralement l'équivalence du plan hyperbolique avec toute surface « abstraite » (techniquement, toute variété riemannienne de dimension 2) de courbure négative constante complète et simplement connexe munie de ses géodésiques ; ce résultat est un cas particulier de son théorème d'uniformisation.

Domaine fondamental et ses images pour l'action du groupe modulaire sur le demi-plan de Poincaré.

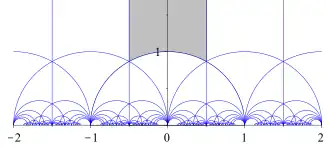
Le groupe modulaire agit naturellement sur le plan hyperbolique, plus particulièrement sur les représentations de Poincaré ; c'est un sous-groupe de son groupe des déplacements, représenté dans ces modèles par les transformations de Möbius. Les courbes modulaires sont définies comme quotients du plan hyperbolique par certains sous-groupes du groupe modulaire ; les classes d'équivalence correspondantes amènent à des pavages du plan hyperbolique, étudiés en particulier par Poincaré, Dedekind et Klein[49].

Le flot géodésique sur une variété riemannienne compacte à courbure négative est le prototype de système dynamique à temps continu le plus chaotique qui soit, une propriété remarquée dès 1898 par Hadamard[50]. On sait aujourd'hui que ce flot est bernoullien[51], et donc en particulier ergodique, mélangeant (« mixing »), etc.[52] - [53]. De nombreuses études détaillées de ce flot et de ses applications ont été publiées à partir de la fin des années 1980[58].

La théorie de la complexité, sous sa forme usuelle, suppose un monde où les signaux se propagent instantanément, et où, par conséquent, la lecture d'une donnée prend toujours le même temps. Mais des analyses plus fines ont été proposées ; il a alors été remarqué que dans un monde hyperbolique, on peut stocker beaucoup plus d'informations à distance donnée, ce qui permet d'accélérer certains calculs ; en particulier, on peut démontrer que, dans cet espace, P = NP[note 31] (cela ne permet pas de démontrer le résultat dans un espace euclidien dans lequel d'ailleurs, très probablement, P est différent de NP)[59].

Dès 1908, Hermann Minkowski a remarqué que l'espace des vecteurs-vitesses de la relativité restreinte se comportait comme le plan hyperbolique (c'est le modèle de l'hyperboloïde)[42]. La composition des vitesses donne naissance ainsi à une structure algébrique appelée espace de gyrovecteurs, définie et étudiée à partir des années 2000 par plusieurs auteurs dont Abraham A. Ungar[47], et qui a trouvé des applications en géométrie hyperbolique proprement dite, mais aussi, par exemple, dans l'étude de la sphère de Bloch[60].

Gauss, puis Lobatchevski, ont envisagé que la géométrie de l'espace physique ne soit pas euclidienne[note 9] - [note 10], mais les mesures géodésiques et même astrométriques qu'ils ont pu réaliser[note 32] n'ont fait que confirmer l'axiome des parallèles. La question a été reprise d'un point de vue physique lorsque Einstein a formulé sa théorie de la relativité générale, dont le modèle suppose que les masses « courbent » l'espace. Déterminer la géométrie de l'espace dans son ensemble, et en particulier sa courbure[note 33], devient alors une question susceptible de tests expérimentaux, utilisant en particulier le fait que dans un espace hyperbolique, le volume d'une sphère croit beaucoup plus vite que le cube de son rayon. Au début du 21^e siècle, l'espace semble cependant « plat » (euclidien) à la précision des mesures[61], ce que nos connaissances physiques actuelles n'expliquent pas bien : c’est le problème de la platitude[note 34]. Pourtant, certains cosmologistes, comme Jean-Pierre Luminet, ont proposé, sous le nom d'« univers chiffonné »[63], des modèles d'univers dont certains sont dérivés de l'espace hyperbolique H³ (en en construisant un espace quotient)[65], et qu'ils affirment compatibles avec les données observationnelles[66].

Si beaucoup de textes de science-fiction et de fantastique font référence à des géométries non-euclidiennes (Lovecraft mentionnant à plusieurs reprises que leur utilisation dans l'architecture par les Grands Anciens rend fous ceux qui essaient de la comprendre[67]), il semble que seul le roman de Christopher Priest, Le Monde inverti, se déroule dans un univers (la surface d'une caténoïde) à géométrie hyperbolique. On peut cependant également citer le Géométricon, une bande dessinée racontant les aventures d'Anselme Lanturlu dans des espaces courbes, parmi lesquels figure le plan hyperbolique[68].

Une collection de plans hyperboliques réalisés au crochet par Margaret et Christine Wertheim, imitant un récif corallien.

Maurits Escher, grâce aux outils que lui a fourni Harold Coxeter en 1952, a utilisé à plusieurs reprises des pavages du plan hyperbolique en transformant leurs motifs pour en faire des figures anthropomorphiques ou des animaux, comme dans Anges et Démons[69], ou dans la série des Limites circulaires[70].

S’inspirant de modèles conçus et réalisés en papier par le géomètre William Thurston[71], Daina Taimiņa a inventé une technique de représentation en crochet de portions du plan hyperbolique, utilisée de manière artistique par Margaret et Christine Wertheim pour imiter des récifs coralliens[72].

• (en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Hyperbolic geometry » (voir la liste des auteurs).

• Marcel Berger, Géométrie 2, Paris, Cassini, coll. « Nouvelle bibliothèque mathématique », 2016, 546 p. (ISBN 978-2-84225-146-8), chap. 19 (partie 2) (« Géométrie hyperbolique »)
• Roger Cuppens, Découvrir les géométries non euclidiennes en jouant avec CABRI, t. 1 : Géométrie Hyperbolique, APMEP (n^o 160), juillet 2007, 128 p. (ISBN 2-912846-37-4, présentation en ligne)
• (en) John Stillwell, Geometry of Surfaces, Springer Verlag, coll. « Universitext », 1992, 236 p. (ISBN 978-0-387-97743-0, lire en ligne)
• (en) Norbert A'Campo et Athanase Papadopoulos, Notes on hyperbolic geometry, Zurich, Société mathématique européenne, coll. « IRMA Lectures in Mathematics and Theoretical Physics » (n^o 18), 2012, 454 p. (ISBN 978-3-03719-105-7, DOI 10.4171/105, lire en ligne), « Strasbourg Master class on Geometry, p. 1-182 »
• (en) Birger Iversen, Hyperbolic Geometry, vol. 25, London Mathematical Society, Cambridge University Press, coll. « Student Texts », 1992, 298 p. (ISBN 0-521-43528-5, lire en ligne).
• (en) Toshitsune Miyake (trad. du japonais), Modular forms, Berlin/Heidelberg/New York, Springer-Verlag, 1989, 335 p. (ISBN 0-387-50268-8).

• Chaos quantique
• Espace métrique hyperbolique
• Formule des traces de Selberg
• Géométrie non euclidienne
• Géométrie elliptique
• Histoire de la géométrie
• Théorème de Hilbert (géométrie différentielle)
• Variété hyperbolique
• Variété riemannienne

• Notices d'autorité :

  • BnF (données)
  • LCCN
  • GND
  • Israël
  • Tchéquie
  • Lettonie
• Notices dans des dictionnaires ou encyclopédies généralistes :

  • Britannica
  • Store norske leksikon
• Rossana Tazzioli, « Les géométries non euclidiennes : histoire et historiographie », sur Images des mathématiques (consulté le 17 avril 2021).
• Jos Leys, « Une chambre hyperbolique », sur Images des mathématiques (consulté le 17 avril 2021).
• « Promenade non euclidienne », sur ENS Lyon (consulté le 17 avril 2021) (conférence donnée par Charles Boubel en 2005).
• David Madore, « Labyrinthes dans le plan hyperbolique », sur madore.org (consulté le 17 avril 2021) (avec des commentaires mathématiques en anglais).
• « Géométries non euclidiennes », sur cabri.net (consulté le 16 avril 2021), constructions détaillées utilisant le logiciel Cabri Géomètre.
• (en) « Hyperbolic geometry », sur université de Glasgow (consulté le 17 avril 2021), site interactif donnant des démonstrations et permettant également des constructions et des calculs dans le modèle du disque de Poincaré.