Apeirogone
En géométrie, un apeirogone (du grec ancien : "ἄπειρος" apeiros : infini, sans bornes, et "γωνία" gonia : angle) est un polygone généralisé ayant un nombre infini (dénombrable) de côtés. Le plus souvent, le terme désigne un polygone régulier convexe (tous les angles et tous les côtés sont égaux, et les côtés ne se croisent pas) ; il n'existe pas à ce sens d'apeirogone non trivial en géométrie euclidienne, mais il y en a plusieurs familles (non semblables les unes aux autres) en géométrie hyperbolique.
| Apeirogone | |
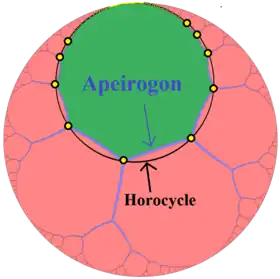 Représentation d'un apeirogone (régulier) dans le modèle du disque de Poincaré | |
| Type | Polygone régulier |
|---|---|
| Arêtes | ∞ |
| Sommets | ∞ |
| Symbole de Schläfli | {∞} |
Définitions
Géométrie euclidienne
H. S. M. Coxeter part de la donnée, dans un espace euclidien, d'un point de base A0 et d'une translation S ; l'ensemble des itérés Ai = Si(A0) (avec ) et des arêtes reliant les sommets adjacents et définit un apeirogone (régulier)[1]. On peut aussi interpréter cette construction comme le partage d'une droite en segments d'égale longueur[2].
Géométrie hyperbolique
La construction classique d'un polygone régulier du plan euclidien (par une suite de rotations de autour d'un centre bien choisi) peut s'adapter en itérant des rotations du segment autour du point et d'angle (le point devenant le point ) ; si on remplace ce dernier angle par un angle quelconque, on n'obtient qu'un polygone régulier étoilé, ou une ligne polygonale ne se refermant pas, mais restant inscrite dans une couronne circulaire. En revanche, en géométrie hyperbolique (et en prenant pour courbure ), si on part d'un côté de longueur a et d'un angle [3], la suite des segments s'éloigne à l'infini ; l'ensemble des , qu'on appelle un apeirogone d'angle et de côté a, est inscrit dans un horocycle si , et dans un hypercycle si (certains auteurs réservent le nom d'apeirogone à ceux inscrits dans des horocycles).
Définition abstraite
Un polytope abstrait est un ensemble partiellement ordonné d'objets (les faces) dont la relation d'ordre modélise l'inclusion des faces de polytopes concrets[4]:22–25. Le cas particulier des polygones abstraits correspond à un ordre partiel sur certains sous-ensembles d'un ensemble de sommets : les sommets eux-mêmes, certains ensembles de deux sommets (les arêtes) et les deux sous-ensembles triviaux vide et plein, chaque sommet appartenant exactement à deux arêtes, et le graphe formé des sommets et des arêtes étant connexe[4]:22–25[5]:224 ; si l'ensemble des sommets est infini dénombrable, on parle d'un apeirogone abstrait[4]:25; il est unique à isomorphisme près. Le groupe des automorphismes de l'apeirogone abstrait (appelés symétries dans ce cas) est le groupe diédral infini[4]:31.
Réalisations
Définition
Une réalisation d'un polygone abstrait est une application de ses sommets vers des points d'un espace métrique (le plus souvent, l'espace euclidien ou l'espace hyperbolique de dimension n) telle que chaque automorphisme du polygone correspond à une isométrie de l'ensemble des images[4]:121[5]:225 ; deux réalisations sont dites congruentes si la bijection naturelle entre leurs ensembles de sommets est induite par une isométrie des espaces d'arrivée tout entiers[4]:126[5]:229. Ainsi, les définitions concrètes données précédemment sont des réalisations de l'apeirogone abstrait, respectivement dans le plan euclidien et dans le plan hyperbolique, mais bien qu'isomorphes, elles ne sont pas congruentes.
Symétries
Le groupe G des automorphismes d'une réalisation V de l'apeirogone abstrait peut se décrire comme engendré par deux symétries (orthogonales), dont le produit envoie chaque sommet de V sur le suivant : la première symétrie laisse un sommet donné invariant, et la seconde échange deux sommets adjacents et [4]:140–141[5]:231 ; selon la réalisation considérée, il est isomorphe au groupe diédral infini (si V est infini) ou au groupe diédral d'ordre 2n (si V a n éléments).
Notes et références
- (en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Apeirogon » (voir la liste des auteurs).
- H. S. M. Coxeter, Regular polytopes, London, Methuen & Co. Ltd., , p. 45
- Norman W. Johnson, Geometries and transformations, Cambridge University Press, (lire en ligne), « 11: Finite Symmetry Groups », p. 226
- est le double de l'angle de parallélisme en à la médiatrice du segment ; pour cette valeur, les médiatrices de et de sont parallèles asymptotes.
- (en) Peter McMullen et Egon Schulte, Abstract Regular Polytopes, Cambridge University Press, , 1st éd. (ISBN 0-521-81496-0, lire en ligne
 )
) - (en) Peter McMullen, « Realizations of regular apeirotopes », Aequationes Mathematicae, vol. 47, nos 2-3, , p. 223–239 (DOI 10.1007/BF01832961, MR 1268033)
Articles connexes
- Apeirogon (roman) (2020, Colum McCann)
Liens externes
- (en) Eric W. Weisstein, « Apeirogon », sur MathWorld




![{\displaystyle [A_{i},A_{i+1}]}](https://img.franco.wiki/i/a09a06f525d57bf51dd1296acbb039fc286aaea8.svg)











![{\displaystyle [A_{0},A_{1}]}](https://img.franco.wiki/i/4c09111aa4b4485d2e7b1f93ee1b38f8d3aa2f0d.svg)
![{\displaystyle [A_{0},A_{2}]}](https://img.franco.wiki/i/6b96a800d60612296eb43b7369bc38b1063b83eb.svg)