Giovanni Girolamo Saccheri
Giovanni Girolamo Saccheri (prononcé : [dʒoˈvanni dʒiˈrɔlamo sakˈkɛri]) (ou Girolamo Saccheri), né à San Remo en 1667 et mort à Milan en 1733, est un mathématicien italien. Il a entraperçu la possibilité de géométries non euclidiennes. Il était prêtre jésuite.
| Naissance | |
|---|---|
| Décès | |
| Activités |
| A travaillé pour | |
|---|---|
| Ordre religieux | |
| Sport | |
| Maître |
Biographie
Saccheri entre dans la Compagnie de Jésus en 1685 et est ordonné prêtre en 1694. Il enseigne d'abord la philosophie à l'université de Turin de 1694 à 1697, puis, de 1697 à sa mort, la philosophie, la théologie et les mathématiques à l'université de Pavie.
Il est un disciple du mathématicien Tommaso Ceva. Parmi ses ouvrages : Quaesita geometrica (1693), Logica demonstrativa (1697) et Neo-statica (1708). Mais c'est à sa dernière publication, datée de 1733 (l'année de sa mort), que Saccheri doit sa renommée : Euclides ab omni naevo vindicatus (Euclide lavé de toute tache). Parmi ses élèves : Luigi Guido Grandi[1].
Contribution


Peut-on se passer du cinquième postulat ?
Les quatre premiers postulats d'Euclide sont beaux, simples, « évidents ». Le cinquième postulat est complexe, d'énoncé long, d'apparence maladroite : « si une droite, tombant sur deux droites, fait les angles intérieurs du même côté plus petits que deux droits, ces droites, prolongées à l'infini, se rencontreront du côté où les angles sont plus petits que deux droits ». De plus, Euclide lui-même attend d'avoir à démontrer sa proposition 28 pour s'en servir. De là l'idée que ce postulat est de trop, qu'il est en fait démontrable (que c'est un théorème). C'est l'idée qu'eut Saccheri. D'autres l'ont eue également, mais chez Saccheri on semble très près de franchir le pas — qu'il ne franchit pas — vers les géométries non euclidiennes.
En 1733, Saccheri publia : Euclides ab omni naevo vindicatus (Euclide lavé de toute tache). Cette œuvre, tombée dans l'oubli, fut redécouverte au milieu du XIXe siècle par Eugenio Beltrami, qui a su y voir un moment important de l'histoire de la géométrie[2].
L'objectif de Saccheri était de prouver par l'absurde la validité des axiomes d'Euclide (on disait à cette époque « postulats d'Euclide »). Il cherchait à obtenir une contradiction en supposant la fausseté du postulat des parallèles. Il obtint des résultats bizarres, qui ont maintenant le statut de théorèmes de géométrie hyperbolique, tels que l'existence de triangles dont la somme des angles est inférieure à 180°.
Saccheri n'eut cependant pas l'audace de Lobatchevski. Il se garda d'approfondir le sujet et rejeta les résultats qu'il avait découverts, au motif qu'ils contredisaient le sens commun.
On ne sait pas si Saccheri a eu accès aux travaux d'Omar Khayyam[3], qui, six siècles plus tôt, avait fait des considérations analogues et obtenu des conclusions similaires. Ni à ceux de Thābit ibn Qurra, qui, encore plus tôt, avait aussi tenté de prouver le cinquième postulat à partir des quatre autres. Quoi qu'il en soit, les mathématiciens qui, dans la longue histoire des géométries non euclidiennes, se sont attaqués à cette tâche avant l'époque moderne n'ont pu sortir de leur stupéfaction devant l'ampleur du paradigme mis en cause.
Quadrilatère de Saccheri
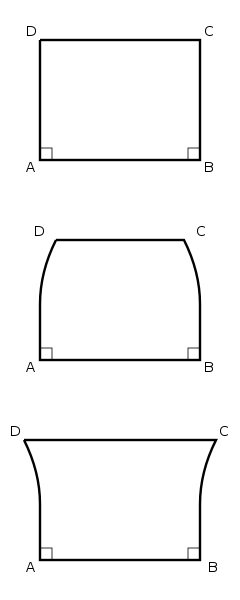
Saccheri veut prouver par l'absurde le postulat des parallèles (ou cinquième postulat). Son point de départ est le quadrilatère birectangle isocèle, à savoir un quadrilatère avec deux côtés opposés congruents et tous les deux perpendiculaires à un seul des autres côtés. Saccheri introduit donc trois hypothèses sur les coins du quadrilatère opposés aux angles droits :
- hypothèse des angles droits : les deux angles sont des angles droits ; cela équivaut à accepter le cinquième postulat ;
- hypothèse des angles obtus : en contradiction avec le cinquième postulat, les deux angles intérieurs sont obtus ;
- hypothèse des angles aigus : en contradiction avec le cinquième postulat, les deux angles intérieurs sont aigus.
L'idée de Saccheri est de réfuter les hypothèses de l'aigu et de l'obtus afin que seule l'hypothèse des angles droits soit possible.
Il réfute l'hypothèse des angles obtus en utilisant le deuxième postulat d'Euclide, admettant ainsi qu'un segment peut être prolongé indéfiniment en ligne droite. Si on renonce à la validité du deuxième postulat, on peut considérer même comme valide l'hypothèse des angles obtus : Riemann lui-même, travaillant sur ce point, en est venu à développer la théorie de la géométrie elliptique. Saccheri pour sa part conclut en disant que « l'hypothèse de l'angle obtus est complètement fausse, car elle se détruit elle-même. »
La réfutation de l'hypothèse des angles aigus par Saccheri est beaucoup plus faible. Il suppose que ce qui vaut pour un point à distance finie de la ligne droite devrait également valoir pour un point « à l'infini », mais cette hypothèse rend effectivement la réfutation inacceptable. Pas trop convaincu, semble-t-il, de sa démonstration, Saccheri la clôt ainsi : « L'hypothèse de l'aigu est absolument fausse, car elle répugne à la nature de la ligne droite. »
Œuvres
Publications scientifiques
- (la) Quaesita geometrica a comite Rugerio de Vigintimillijs omnibus proposita, Milan, 1693
- (la) Vincenzo De Risi (dir.), Euclides ab omni naevo vindicatus, Pise, Edizioni della Normale, 2011 (ISBN 978-88-7642-404-5) — Première édition : 1733
- (it) L'Euclide emendato del p. Gerolamo Saccheri, trad. et notes de G. Boccardini, Milan, U. Hoepli, 1904
- (en) Girolamo Saccheri's Euclides vindicatus, trad. G. B. Halsted, Chicago, Open Court Publishing Company, 1920
- (it) (la) Pierangelo Frigerio (dir.), Euclide liberato da ogni macchia, introduction d'Imre Toth et d'Elisabetta Cattanei, Milan, Bompiani, 2001
- (la) Logica demonstrativa, Pavie (Ticini Regij), typis haeredum Caroli Francisci Magrij, (lire en ligne)
- (la) Neo-statica, Milan, Giuseppe Pandolfo Malatesta, 1708
Écrits de controverse
- (it) Esame teologico contro un libro ingiurioso intitolato Difesa del giudizio formato dalla Santa Sede Apostolica nel dì 20. novembre 1704[5] — En ligne : la deuxième édition (1710).
- (it) Continuazione dell'esame teologico : in cui si risponde a due libri l'uno intitolato Lettera ad un'amico … L'altro intitolato Brevissima controversia … ; con vna appendice nel fine in risposta a tre dichiarazioni di monsig. Maigrot vescovo cononense
- (it) Confermazione teologica : colla quale si prova che il vero pregio della veracità è l'innocenza della medesima nella sicura custodia de' segreti : ove rispondesi all'opera del p. lettore Orsi domenicano, 1729[6]
Bibliographie
- Vincenzo De Risi, « Saccheri, Giovanni Girolamo », dans Enciclopedia Treccani, 2013
- Pierre Duhem, Les origines de la statique, vol. 2, 1905–1906, p. 272
- Claudia Madonia, Les jésuites, histoire et dictionnaire, Paris, Bouquins Editions, 2022, 1328 p. (ISBN 978-2-38292-305-4), p. 1021-1022
Compléments
Voir aussi
Notes et références
- L. Tenca, « Relazioni fra Gerolamo Saccheri e il suo allievo Guido Grandi », dans Studia Ghisleriana, 1952, 1, p. 19–45.
- Eugenio Beltrami, « Un precursore italiano di Legendre e di Lobatschewsky », dans Rendiconti dell’Accademia dei Lincei, 4e série, vol. V, 1er semestre, 1889, p. 441.
- On entend parfois « quadrilatère de Khayyam-Saccheri ».
- Pour le détail des éditions, voir Paolo Pagli, « Two unnoticed editions of Girolamo Saccheri's Logica demonstrativa », dans History and Philosophy of Logic, vol. 30, no 4, 2009, p. 331–340 — Résumé en ligne.
- (it) Difesa del giudizio formato dalla S. Sede Apostolica nel dì 20. Novembre 1704. E pubblicato in Nankino dal Card. di Tournon alli 7. Febbrajo 1707. Intorno a' riti, e cerimonie cinesi. Contro un libello sedizioso intitolato Alcune riflessioni intorno alle cose presenti della Cina. A cui vengono annesse tre appendici, contro le tre scritture latine ultimamente stampáte dalli difensori de' medesimi riti condannati. Le cardinal de Tournon qui est mentionné est Charles Thomas Maillard de Tournon.
- Conjecture de WorldCat.
- C'est aussi Beltrami qui a attribué la paternité de ce théorème à Saccheri : E. D'Ovidio, « Cenno sulla nota del Prof. E. Beltrami : Un precursore italiano di Legendre e di Lobatschewsky », dans Atti della Reale Accademia delle scienze di Torino, vol. 24, p. 513.
Liens externes
- Notices dans des dictionnaires ou encyclopédies généralistes :
- Pages consacrées à Saccheri, site du Centro di ricerca matematica Ennio de Giorgi
- (en) John J. O'Connor et Edmund F. Robertson, « Giovanni Girolamo Saccheri », sur MacTutor, université de St Andrews.
.