Modèle de Klein

Dans le modèle de Klein, les droites de l'espace hyperbolique sont représentées par des segments. Ici, plusieurs droites passent par le point P en étant parallèles à la droite a.

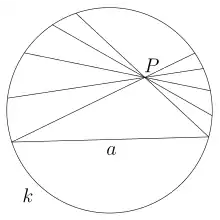
Arthur Cayley a appliqué le birapport de la géométrie projective à la mesure des angles et des distances en géométrie sphérique[3].

Par la suite, Felix Klein a réalisé que l'idée de Cayley s'appliquait aux modèles projectifs non euclidiens[4]. Soient deux points distincts P et Q de la boule unité ouverte, l'unique ligne droite les reliant coupant la sphère unité en deux points A et B tels que les points soient dans l'ordre A, P, Q, B. Alors la distance hyperbolique entre P et Q s'exprime par la valeur absolue du demi-logarithme du birapport (P,Q ; A,B) :

${\displaystyle d(P,Q)={\frac {1}{2}}\log {\frac {|QA||BP|}{|PA||BQ|}}}$,

où la barre verticale indique la distance euclidienne. Cette expression se comporte en effet comme une abscisse sur la droite (A, B). Si ${\displaystyle t={\frac {1}{2}}\log {\frac {|QA||BP|}{|PA||BQ|}}}$ est l'abscisse entre P et Q, et ${\displaystyle u={\frac {1}{2}}\log {\frac {|RA||BQ|}{|QA||BR|}}}$ l'abscisse entre Q et R, alors l'abscisse entre P et R est ${\displaystyle {\frac {1}{2}}\log {\frac {|RA||BP|}{|PA||BR|}}={\frac {1}{2}}\log {\frac {|QA||BP|}{|PA||BQ|}}+{\frac {1}{2}}\log {\frac {|RA||BQ|}{|QA||BR|}}=t+u}$.

Le facteur 1/2 est nécessaire pour que la courbure de Gauss vaille −1. Il permet également d'avoir, au voisinage du centre du disque, une métrique hyperbolique identique à la métrique euclidienne du modèle. Plus généralement, si A est un point du modèle de Klein ayant ${\displaystyle (a_{1},\ldots ,a_{n})}$ pour coordonnées dans ${\displaystyle \mathbb {R} ^{n}}$, et si on pose |A| la norme euclidienne usuelle de A, alors la métrique locale du modèle de Klein au point A est donnée par :

${\displaystyle \mathrm {d} s^{2}={\frac {1}{1-|A|^{2}}}\sum _{i=1}^{n}\mathrm {d} a_{i}^{2}+{\frac {1}{(1-|A|^{2})^{2}}}\left(\sum _{i=1}^{n}a_{i}\mathrm {d} a_{i}\right)^{2}}$.

Lorsque P s'approche du bord, la distance d(P,Q) tend vers l'infini. La sphère limite ne fait donc pas partie de l'espace hyperbolique. Elle représente l'ensemble des points à l'infini.

Représentation de cercles en géométrie hyperbolique, dans le modèle de Klein.

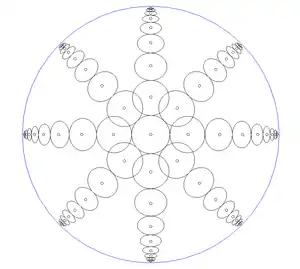
Si les droites de l'espace hyperbolique sont aisées à tracer dans le modèle de Klein, il n'en est pas de même des cercles. En effet, la distance précédemment définie présente l'inconvénient que, lorsqu'on s'approche du bord dans le modèle (ce qui correspond au fait de s'éloigner vers l'infini dans l'espace hyperbolique), un écart donné entre deux points se trouve contracté dans le modèle davantage dans le sens radial que dans le sens orthoradial. Il en résulte que la représentation d'un cercle de l'espace hyperbolique dans le modèle se transforme en une ellipse de plus en plus aplatie au fur et à mesure qu'on s'approche du bord. Il en résulte également une déformation de plus en plus prononcée des angles.

Pour pallier cet inconvénient, on peut recourir à un autre modèle de l'espace hyperbolique, le disque de Poincaré.

Le modèle de l'hyperboloïde est un modèle de géométrie hyperbolique dans un espace de Minkowski de dimension n + 1. La forme bilinéaire symétrique de Minkowski (qui n'est pas un produit scalaire) est donnée par :

${\displaystyle \mathbf {x} \cdot \mathbf {y} =x_{0}y_{0}-x_{1}y_{1}-\cdots -x_{n}y_{n}\,}$

et la pseudo-norme par ${\displaystyle \|\mathbf {x} \|={\sqrt {\mathbf {x} \cdot \mathbf {x} }}}$. L'espace hyperbolique de dimension n est constitué des éléments x de l'espace de Minkowski vérifiant ||x|| = 1 et x₀ positif, qui forment une nappe d'un hyperboloïde. La distance intrinsèque entre les points u et v est donnée par :

${\displaystyle d(\mathbf {u} ,\mathbf {v} )=\cosh ^{-1}(\mathbf {u} \cdot \mathbf {v} )}$.

On peut également écrire cela sous la forme homogène

${\displaystyle d(\mathbf {u} ,\mathbf {v} )=\cosh ^{-1}\left({\frac {\mathbf {u} }{\|\mathbf {u} \|}}\cdot {\frac {\mathbf {v} }{\|\mathbf {v} \|}}\right)}$,

qui permet de redimensionner les vecteurs à volonté.

Le modèle de Beltrami–Klein est obtenu à partir de cet hyperboloïde en redimensionnant tous les vecteurs de façon que la pseudo composante de temps x₀ soit 1, c'est-à-dire, en projetant l'hyperboloïde depuis l'origine sur le plan x₀ = 1. Ceci transforme l'hyperboloïde en une boule de rayon 1 dont le bord correspond aux points à l'infini.

On passe du modèle de Klein (où les droites hyperboliques sont représentées par des segments, en jaune) au modèle de Poincaré (où les droites hyperboliques sont représentées par des arcs de cercles, en rouge) de la façon suivante : projeter les points du modèle de Klein sur la demi-sphère (en bleu) dont le modèle de Klein est le disque équatorial, puis procéder à une projection stéréographique depuis le pôle sud pour ramener ces points dans le plan équatorial. Le schéma illustre cette transformation géométrique.

Le disque de Poincaré et le modèle de Klein sont deux modèles de l'espace hyperbolique de dimension n en forme de boule unité. Cependant, dans le modèle de Klein, les droites hyperboliques sont des segments, alors que dans le modèle de Poincaré, ce sont des arcs de cercle.

On passe géométriquement d'un modèle à l'autre en se plaçant dans un espace de dimension n+1. On projette le modèle de Klein sur un hémisphère dont le modèle de Klein est un disque équatorial, perpendiculairement à ce disque. Les segments du modèle représentant les droites hyperboliques sont alors transformés en arcs de cercles de l'hémisphère. On procède ensuite à une projection stéréographique depuis le pôle sud de la sphère sur le disque équatorial. Cette projection transforme les arcs de cercle de l'hémisphère en arcs de cercle du disque équatorial. Ces derniers sont les droites hyperboliques dans le modèle de Poincaré.

On peut aussi passer par le modèle de l'hyperboloïde, celui-ci donnant soit le modèle de Klein soit le disque de Poincaré selon la projection utilisée. Le modèle de Klein est obtenu en projetant l'hyperboloïde ${\displaystyle x_{0}^{2}=x_{1}^{2}+\dots +x_{n}^{2}+1}$ depuis l'origine sur le plan ${\displaystyle x_{0}=1}$, le disque de Poincaré est obtenu en projetant le même hyperboloïde depuis le point (–1, 0, ..., 0) sur le plan ${\displaystyle x_{0}=0}$.

Analytiquement, si un point du modèle de Klein est donné par ses coordonnées cartésiennes A, son image B dans le disque de Poincaré vaut ${\displaystyle B={\frac {A}{1+{\sqrt {1-A^{2}}}}}}$ où ${\displaystyle A^{2}}$ représente le carré scalaire euclidien de A. Réciproquement, on a ${\displaystyle A={\frac {2B}{1+B^{2}}}}$. On remarque que A et B restent constamment alignés avec le centre du disque.

• (es) Luis Santaló, Geometrias no Euclidianas (en), EUDEBA, 1961
• (en) Saul Stahl, The Poincaré Half-Plane, Jones and Bartlett, 1993