La sphère de Bloch, du nom du physicien et mathématicien Félix Bloch, ou sphère de Poincaré (comme cas d'application de celle-ci), est une représentation géométrique d'un état pur d'un système quantique à deux niveaux ; c'est donc, entre autres, une représentation d'un qubit. Il est possible de généraliser la construction de cette sphère à un système à  niveaux.
niveaux.
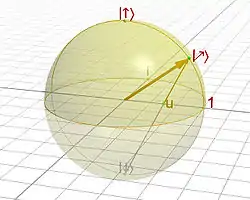
L'état d'un système à deux niveaux, tel qu'un
spin 1/2 ou plus généralement un
qubit, peut être représenté par un point sur une sphère.
La mécanique quantique se formalise dans les espaces de Hilbert, ou plus exactement, dans les espaces de Hilbert projectifs. L'espace projectif des états purs d'un système à 2 niveaux est isomorphe à une sphère.
La métrique naturelle de la sphère de Bloch est la métrique de Fubini-Study.
Le qubit

État quantique représenté sur la sphère de Bloch, accompagné de ses coordonnées sphériques φ et θ.
Considérons un état pur  d'un système à deux niveaux. En toute généralité, on peut le décomposer sur les états propres de l'espace
d'un système à deux niveaux. En toute généralité, on peut le décomposer sur les états propres de l'espace  et
et  par :
par :  avec
avec  et
et  . De plus, puisque les facteurs de phase n'affectent pas l'état physique d'un système, nous pouvons sans perte de généralité supposer
. De plus, puisque les facteurs de phase n'affectent pas l'état physique d'un système, nous pouvons sans perte de généralité supposer  réel positif, et réécrire
réel positif, et réécrire  avec
avec 
Cette représentation décrit ψ sans ambiguïté. Les paramètres  et
et  spécifient de manière unique un point sur la sphère unité de
spécifient de manière unique un point sur la sphère unité de  ayant pour coordonnées cartésiennes :
ayant pour coordonnées cartésiennes :
 .
.
Dans cette représentation,  et
et  .
.
De plus, on peut calculer  et
et 



















