Sphère de Poincaré
La sphère de Poincaré est un formalisme utilisé en optique pour représenter l'état de polarisation de la lumière. Il a été présenté en 1892 dans l'ouvrage du mathématicien Henri Poincaré Théorie mathématique de la lumière[1].
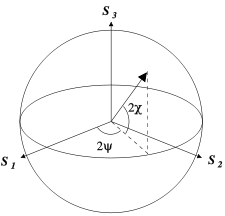
Cette représentation est aussi utilisable pour des lumières partiellement polarisées. Un point sur la sphère de rayon unité représente une polarisation donnée.
Coordonnées
Le rayon I.R d'un état de polarisation indique la quantité de polarisation de la lumière, où I = S0 est la quantité de lumière totale, et (I x R)2 = (S12+S22+S32) la quantité de lumière polarisée.
- Pour une lumière dépolarisée, R=0
- Pour une lumière entièrement polarisée, R=1
- Entre ces deux valeurs la lumière est partiellement polarisée.
L'angle caractérise l'azimut de la polarisation de la lumière et l'angle caractérise son ellipticité.
(Voir aussi Paramètres de Stokes).
Représentations particulières
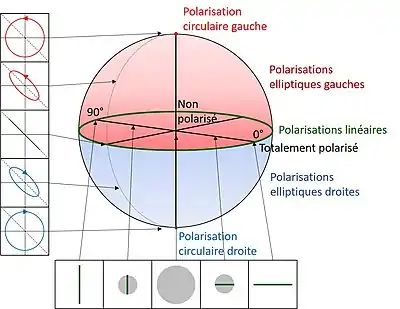
- La partie supérieure de la sphère représente des polarisations gauches et la partie inférieure représente des polarisations droites[2].
- Le plan de l'équateur de la sphère (OS1S2) représente l'ensemble des polarisations linéaires. En particulier, du fait de l'utilisation d'un angle des polarisations orthogonales sont représentées diamétralement opposées.
- Les pôles de la sphère représentent des polarisations circulaires. Le pôle Nord représente la polarisation circulaire gauche et le pôle sud représente la polarisation circulaire droite.
- Un même méridien représente l'ensemble des polarisations d'azimut constant.
Lames d'onde
La sphère de Poincaré permet la représentation de l'action des lames d'onde.
- Une lame demi-onde correspond pour la sphère de Poincaré à une symétrie de l'état de polarisation par rapport au méridien de l'axe neutre de la lame.
- Une lame quart d'onde correspond sur la sphère à une rotation de 90° autour de l'axe rapide de la lame dans le sens direct.


