Rotation (physique)

Système géocentrique de Ptolémée

Dans la pensée des anciens grecs, les mouvements des planètes (au sens ancien, le mot planète inclut le Soleil et la Lune, mais pas la Terre) doivent être parfaits, donc seul le mouvement circulaire était autorisé, par opposition aux mouvements angulaires ou rectilinéaires qui étaient considérés comme forcés.

La théorie des épicycles compose des mouvements de rotation : les planètes tournent sur des roues appelées épicycles ; lesquels tournent eux-mêmes sur une autre roue, appelée déférent, dont le centre est la Terre. La rotation simultanée des deux permettait d'obtenir un mouvement complexe, éventuellement rétrograde, et d'expliquer celui des planètes et de la Lune, en préservant en grande partie les présupposés philosophiques de l'époque : les mouvements des astres sont circulaires, centrés sur la terre et de vitesse uniforme.

L'orbite circulaire n'est qu'une approximation du mouvement képlérien, lequel est bien mieux décrit par des trajectoires elliptiques — même si, après tout, la décomposition en série de Fourier montre qu'à partir du moment où le mouvement est considéré comme périodique, il peut être décrit comme la superposition d'une série (infinie) de mouvements circulaires.

En ramenant les bras dans l'axe du corps, le patineur diminue son moment d'inertie, ce qui —à cause de la conservation du moment cinétique— augmente inversement sa vitesse de rotation.

Pour la physique moderne, la rotation dans l'espace reste un élément déterminant des grands principes gouvernant les lois de la physique, mais le mouvement circulaire uniforme n'a plus de prééminence particulière.

Dans les grands principes de symétrie gouvernant la physique, celui de l'isotropie de l'espace, veut que les lois de la physique ne dépendent pas du lieu de l'observation ni de l'orientation de l'observateur. Un principe plus fort, le principe cosmologique, suppose même que l'univers lui-même est isotrope à suffisamment grande échelle, c'est-à-dire que le contenu observable n'y dépend ni de la position de l'observateur, ni de la direction d'observation.

Un espace homogène signifie en particulier qu'il n'y a pas de direction absolue dans l'espace, et donc, que les lois de la physique sont invariantes par une rotation dans l'espace.

Cette invariance implique en particulier que le lagrangien d'un système physique est invariant en rotation. Le théorème de Noether, qui dit que « à toute transformation infinitésimale qui laisse invariante l'intégrale d'action correspond une grandeur qui se conserve », permet alors de montrer qu'une certaine grandeur physique est conservatoire pour un système isolé : c'est ainsi que la conservation du moment cinétique peut se démontrer à partir de l'invariance en rotation.

Quand un système physique isolé tourne, il le fait en permanence et son moment cinétique est invariant. Il n'y a donc aucune périodicité ni aucune variation intrinsèque dans un tel mouvement, par rapport à son moment cinétique. Et, en particulier, un mouvement en rotation uniforme est essentiellement uniforme, son « passage » sur un nombre de tours est un accident lié au repérage que l'on en fait dans un repère galiléen ; mais intrinsèquement, le fait d'avoir tourné de « un tour » n'est pas plus pertinent que le fait d'avoir tourné de « un radian » ou de « un degré » : ces jalons sont des non-événements pour le mouvement de rotation.

Rotation plane autour d'un axe fixe

En dynamique du solide, l'étude première est celle de la mécanique du point, où l'on voit apparaître les concepts de vitesse, de force, de masse, et d'accélération associée. Dans toutes ces modélisations, on suppose que le système physique étudié est de taille « négligeable », c'est-à-dire, très exactement, non pas vraiment qu'il est ponctuel, mais plus exactement, que la variation de sa rotation n'intervient pas dans la description du système. L'étude du mouvement de rotation suppose au contraire que le système physique est de taille notable, et que l'évolution de sa rotation dans l'espace est une donnée importante de la description.

Le mouvement de rotation dont l'étude est la plus simple est celui d'une rotation autour d'un axe fixe : c'est le mouvement d'un tourne-disque, d'un manège de fête foraine, ou d'un ventilateur à pales.

Dans un tel mouvement, un point du solide, repéré en coordonnées polaires par rapport à l'axe de rotation par un angle et sa distance, voit l'angle varier avec le temps, sans que la distance ne soit modifiée.

Il existe une similitude entre la description cinématique d'un mouvement linéaire et celle d'un mouvement de rotation :

• Là où un point matériel peut être décrit par son vecteur position, qui a la dimension d'une longueur, un solide doit de plus être décrit par son orientation dans l'espace, qui a la nature d'un écart angulaire (et s'exprime normalement en radian).
• La vitesse du point est la variation temporelle de sa position ; et sa vitesse angulaire est de même la dérivée de son orientation par rapport au temps, exprimée en radian par seconde. Si cette vitesse est constante, le mouvement est celui d'un mouvement circulaire uniforme.
• De même qu'un mouvement non uniforme est caractérisé par son accélération, un mouvement circulaire non uniforme subit une accélération angulaire (en rad.s⁻²).

Cependant, la simple lecture d'un angle ne suffit pas à caractériser une rotation : il faut également connaître la direction de l'axe de rotation pour pouvoir relier à une rotation définie l'écart constaté entre deux directions de l'espace tridimensionnel.

Il y a une traduction directe entre vitesse de rotation et fréquence, mais il n'y a pas d'identité : ce sont deux grandeurs physiques différentes, l'une orientée et l'autre non.

La grandeur physique qui caractérise un corps en rotation est sa vitesse de rotation. Étant la variation temporelle de l'orientation, elle s'exprime comme une unité angulaire divisée par une unité de temps.

L'unité du système international d'unités est le radian par seconde. D'autres unités sont d'usage courant, par exemple le tour par minute, le degré par heure...

Il est important de remarquer que le mouvement circulaire uniforme d'un corps solide est par essence uniforme, et que le fait qu'un des points du système physique ait parcouru « un tour » n'a pas plus de signification que de dire qu'il a parcouru « un degré » ou « un radian ». De ce fait, s'il est exact de dire que la position d'un point particulier varie périodiquement, et que cette position peut donc avoir une période et une fréquence définie, le mouvement de rotation par lui-même n'est pas un phénomène périodique, et n'a pas de fréquence.

La différence peut se noter dans l'unité associée à ces grandeurs différentes : la fréquence est une grandeur scalaire mesurée en hertz. Une rotation physique est au contraire une grandeur vectorielle (et plus exactement un pseudovecteur, ce qui sera détaillé plus loin), parce qu'elle est liée à une certaine orientation dans l'espace de son axe de rotation ; et elle s'exprime en radian par seconde. Il est évident qu'il existe une correspondance entre les deux : si une roue en rotation uniforme ω (en rad.s⁻¹) est affectée d'un balourd, la vibration qu'elle va provoquer aura effectivement une fréquence de 2πω (en hertz), mais il ne s'agit pas de la même grandeur physique, parce que l'on ne peut pas confondre une rotation (intrinsèquement orientée) et une fréquence (scalaire intrinsèquement sans orientation). De fait, on voit parfois des vitesses de rotation être mesurées en hertz : il faut comprendre, dans ce cas, que l'unité sous-entendue dans la mesure est en réalité le nombre de tours par seconde.

Il existe une troisième unité qui a la dimension de l'inverse d'un temps, c'est la fréquence angulaire, une notion que l'on rencontre notamment avec la fonction d'onde de la physique quantique, qui n'est pas vectorielle (donc, n'est pas une vitesse de rotation), mais n'est pas réellement une fréquence non plus (il s'agit d'un pseudoscalaire, distinct des deux précédents).

La description physique d'une rotation dans l'espace demande que soit précisé l'axe de rotation.

Dans l'espace, une roue tourne dans le sens des aiguilles d'une montre, ou dans l'autre, suivant le côté d'où on la regarde.

Dans un corps solide en rotation, chaque point a sa propre vitesse, qui d'un point à l'autre peut changer de direction ou d'intensité : les vitesses forment ce que l'on appelle un champ vectoriel. Cependant, le corps étant « solide », la répartition des vitesses ne peut pas être quelconque, mais doit laisser invariante la distance entre deux points quelconques de ce solide.

Considérons le champ des vecteurs vitesse des points d'un solide ${\displaystyle \scriptstyle {\vec {v}}}$ à un instant donné. Si l'on considère deux points A et B, le segment [AB] garde la même longueur, c'est-à-dire que :

${\displaystyle {\begin{aligned}{\mathrm {d} \over \mathrm {d} t}\left({\overrightarrow {AB}}\right)^{2}=0&=2.{\overrightarrow {AB}}.{\mathrm {d} \over \mathrm {d} t}\left({\overrightarrow {AB}}\right)\\&=2.{\overrightarrow {AB}}.\left({\overrightarrow {\mathrm {d} B \over \mathrm {d} t}}-{\overrightarrow {\mathrm {d} A \over \mathrm {d} t}}\right)\\&=2.{\overrightarrow {AB}}.\left({\vec {v}}_{B}-{\vec {v}}_{A}\right)\end{aligned}}}$

Il en résulte que pour tout couple AB de points du solide, la projection sur ${\displaystyle \scriptstyle {\overrightarrow {AB}}}$ de ${\displaystyle \scriptstyle {\vec {v}}(\mathrm {A} )}$ et de ${\displaystyle \scriptstyle {\vec {v}}(\mathrm {B} )}$ sont identiques, le champ est ce que l'on appelle un « champ équiprojectif » :

${\displaystyle \forall (A,B),\qquad {\vec {v}}_{A}\cdot {\overrightarrow {\mathrm {AB} }}={\vec {v}}_{B}\cdot {\overrightarrow {\mathrm {AB} }}}$

Le champ des vitesses ayant la propriété d'être équiprojectif, c'est ce que l'on appelle un torseur. On peut montrer que dans ce cas, le champ des vitesses est entièrement défini par deux choses : sa valeur en un point (que l'on peut par exemple choisir comme le centre de gravité du système) ; et un vecteur que l'on appelle la « résultante » du torseur, notée ici ${\displaystyle \scriptstyle {\overrightarrow {\Omega }}}$. Connaissant la vitesse au point A, celle du point B est alors donnée par :

${\displaystyle {\vec {v}}_{B}={\vec {v}}_{A}+{\overrightarrow {\Omega }}\wedge {\overrightarrow {AB}}}$

On montre de plus que l'ensemble des points où la vitesse ainsi calculée est colinéaire au vecteur ${\displaystyle \scriptstyle {\overrightarrow {\Omega }}}$ est une droite, qui est l'axe instantané de rotation du système (qui dans le cas général peut varier avec le temps). On peut démontrer en outre que dans le cas d'un système isolé, cet axe de rotation (qui n'est généralement pas fixe, dans le cas de mouvement à la Poinsot ) passe par le centre de gravité du système en rotation.

Règle de la main droite :
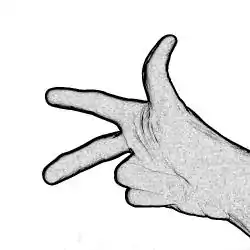
Par convention, le pouce est dans le sens du vecteur rotation indiqué par l'enroulement des doigts.

Physiquement, donc, la simple donnée d'une vitesse de rotation scalaire ne permet pas de caractériser complètement le mouvement de rotation d'un solide en trois dimensions, parce que ce mouvement est intrinsèquement lié à une directionnalité, celle de l'axe de rotation. L'association d'un scalaire et d'une direction correspond à la notion de vecteur, la définition complète du mouvement de rotation aura ainsi naturellement un caractère vectoriel.

Cependant, si la direction d'un axe de rotation est une donnée physique objective, cette direction n'est pas orientée, et elle n'impose pas le sens dans lequel une rotation doit être comptée. Suivant que l'on regarde le long de l'axe d'un côté ou de l'autre, la même rotation apparaîtra comme allant dans le sens des aiguilles d'une montre, ou dans le sens contraire, c'est-à-dire que la valeur de la rotation devra être comptée positivement ou négativement.

Par convention, la représentation d'une rotation sera un vecteur ${\displaystyle \scriptstyle {\overrightarrow {\Omega }}}$ porté par l'axe de rotation, de norme égale à la vitesse de rotation ${\displaystyle \scriptstyle \omega }$, et dont le sens est donné par la règle de la main droite : suivant cette convention, si le pouce marque l'axe, il pointe dans le sens d'une rotation allant dans le sens de l'enroulement des doigts.

On peut noter qu'avec cette convention, le vecteur rotation de la Terre est dirigé vers le pôle nord. De même, la rotation de la Lune autour de la Terre, de celle-ci autour du Soleil, ainsi que de toutes les planètes et la plupart des lunes, est orientée vers le nord de la sphère céleste.

Image miroir d'un système physique comportant un pseudovecteur B : le résultat est l'image miroir de B, qui de plus change de signe, à cause de la convention d'orientation.

L'autre règle de la main droite : le repère (pouce, index, majeur) est dans le sens direct.

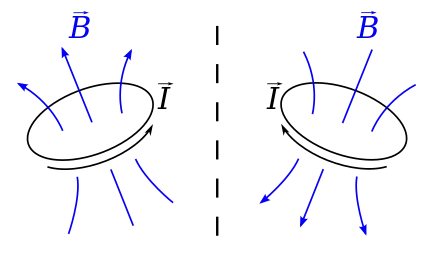
Comme souligné ci-dessus, une rotation est une grandeur physique qui présente un caractère d'orientation marqué, puisqu'elle est nécessairement associé à la direction d'un axe de rotation. Étant défini par une norme et une direction, une rotation peut être représentée par un vecteur. Mais ce n'est pas un vecteur vrai, au sens physique du terme, comme le sont un déplacement, une vitesse, ou un champ électrique, lesquels sont entièrement déterminés par la physique du système.

Ici, l'axe de rotation donne bien une direction, mais laisse indéterminé le sens suivant lequel doit être compté le vecteur. Ce sens n'est pas donné par la physique du système, mais par une convention : celle de la règle de la main droite, qui gouverne le sens dans lequel doit être compté un produit vectoriel ou une rotation. C'est pour cette raison que l'on dit que la rotation est un pseudovecteur, non un vecteur vrai.

Le caractère « non déterminé physiquement » d'un pseudovecteur transparaît dans ce qui se passe si le système physique est remplacé par son image dans un miroir ou par une symétrie centrale. Les règles de la physique sont normalement indépendantes du choix d'un repère pour les exprimer, et donc, pour tout ce qui est physiquement déterminé, on devrait avoir la même expression, que le repère (i, j, k) soit direct, c'est-à-dire corresponde à l'ordre des doigts de la main droite, ou indirect, c'est-à-dire l'image miroir (ou par une symétrie centrale) du précédent, qui reflète l'ordre de la main gauche.

Ce n'est pas le cas du sens de rotation : si l'on prend l'image dans un miroir d'une boucle I tournant dans le sens direct et du vecteur ${\displaystyle \scriptstyle {\vec {B}}}$ représentant cette rotation, l'image de la boucle tournera dans le sens inverse, et le vecteur représentant cette rotation devra d'une part subir la symétrie physique, mais de plus change de signe à cause de la convention d'orientation.

Cette convention sur le sens de rotation est celle du sens trigonométrique direct : si l'espace est repéré par un repère direct ${\displaystyle \scriptstyle ({\vec {i}},{\vec {j}},{\vec {k}})}$, une rotation dans le plan ${\displaystyle \scriptstyle ({\vec {i}},{\vec {j}})}$ qui amène le vecteur ${\displaystyle \scriptstyle {\vec {i}}}$ sur ${\displaystyle \scriptstyle {\vec {j}}}$ est une rotation dite « directe », et son vecteur représentatif est dans le sens du vecteur ${\displaystyle \scriptstyle {\vec {k}}}$. C'est également la même convention qui donne le sens d'un produit vectoriel : si le repère ${\displaystyle \scriptstyle ({\vec {i}},{\vec {j}},{\vec {k}})}$ est direct, donc représenté dans cet ordre par la main droite, le produit vectoriel ${\displaystyle \scriptstyle {\vec {i}}\wedge {\vec {j}}}$ se représente dans la même direction que le vecteur ${\displaystyle \scriptstyle {\vec {k}}}$.

Remarque : il est parfois d'usage de noter les pseudovecteurs par une flèche courbe ${\displaystyle \scriptstyle {\overset {\hookrightarrow }{P}}}$ et non une flèche vectorielle ${\displaystyle \scriptstyle {\vec {P}}}$ pour les distinguer des vecteurs vrais, et rappeler leur lien avec la convention sur le sens de rotation. Cet usage ne semble cependant jamais suivi pour les mouvements de rotation, que ce soient la vitesse de rotation, sa dérivée l'accélération angulaire, ou son intégrale l'écart angulaire, dont le lien avec le sens de rotation est suffisamment évident.

Mise en mouvement de rotation dans un exercice de jonglage. La rotation rapide autour de l'axe principal d'inertie du cerceau stabilise son attitude.

De même que la mise en mouvement rectiligne d'un solide suppose l'existence d'une Force, une mise en rotation suppose l'existence d'un couple produisant un moment ${\displaystyle \scriptstyle {\overset {\hookrightarrow }{\mathcal {M}}}}$ non nul. Comme le montre le théorème du moment cinétique, la dérivée temporelle du moment cinétique ${\displaystyle \scriptstyle {\overset {\hookrightarrow }{L}}_{\mathrm {O} }}$ par rapport à un point O (le plus souvent pris comme le centre de gravité du système) est alors égale au moment global ${\displaystyle \scriptstyle {\overset {\hookrightarrow }{\mathcal {M}}}}$, par rapport au même point, des forces appliquées :

${\displaystyle {\mathrm {d} \over \mathrm {d} t}({\overset {\hookrightarrow }{L}}_{\mathrm {O} })={\overset {\hookrightarrow }{\mathcal {M}}}_{\mathrm {O} }}$

Dans le domaine de la rotation, cette relation est l'analogue de celle disant que pour le mouvement du point matériel, la dérivée temporelle de la quantité de mouvement est égale à la somme des forces appliquées au système.

Le moment cinétique d'un solide idéal est relié à son vecteur rotation ${\displaystyle \scriptstyle {\vec {\omega }}}$ à travers son tenseur d'inertie (ou moment d'inertie) ${\displaystyle \scriptstyle {\overset {=}{I}}}$, par la relation matricielle :

${\displaystyle {\overset {\hookrightarrow }{L}}_{\mathrm {O} }={\overset {=}{I}}\cdot {\vec {\omega }}}$

Ici, le moment d'inertie joue dans le mouvement de rotation le même rôle que la masse dans le mouvement du point matériel. Il représente l'inertie qu'il faut vaincre pour mettre le système en mouvement de rotation, c'est-à-dire lui faire subir une accélération angulaire :

${\displaystyle {\overset {\hookrightarrow }{\mathcal {M}}}_{\mathrm {O} }={\mathrm {d} \over \mathrm {d} t}({\overset {\hookrightarrow }{L}}_{\mathrm {O} })={\overset {=}{I}}\cdot {\mathrm {d} \over \mathrm {d} t}({\vec {\omega }})}$

Le tenseur d'inertie est une caractéristique propre du solide (S), et donne la répartition des masses en son sein. Il s'agit d'un tenseur symétrique. Du fait de son caractère symétrique, il est toujours possible de diagonaliser ce tenseur par un choix judicieux des axes, qui sont appelés alors axes principaux d'inertie. Cependant il s'agit d'un tenseur, ce qui signifie que dans le cas général, le vecteur instantané de rotation ${\displaystyle \scriptstyle {\vec {\omega }}}$ n'est pas colinéaire au moment cinétique. C'est une propriété du mouvement à la Poinsot qui apparaît clairement dans l'effet Djanibekov, et que l'on peut reproduire à domicile en faisant tourner un paquet de cartes à jouer (dont les trois moments d'inertie sont différents) autour de l'axe d'inertie intermédiaire.

Des modifications du moment d'inertie d'une roue sont nécessaires pour son Équilibrage statique et dynamique.

Dans le cas où l'on impose à un solide un axe de rotation, ce qui est typiquement le cas d'une roue de voiture, un équilibrage est nécessaire pour éviter que le mouvement de rotation de ce solide n'impose des efforts anormaux sur les paliers qui guident son mouvement en rotation et lui imposent un axe de rotation. Cet équilibrage est l'une des préoccupations de la théorie des machines tournantes.

Un premier équilibrage est assez évident, l'« équilibrage statique », qui consiste à aligner le centre de gravité du système mobile sur l'axe de rotation. Si en effet cet alignement n'est pas réalisé, la rotation du système physique imposée autour d'un axe qui ne contient pas son centre de gravité entraînera un balourd[1]. Physiquement, le maintien mécanique de l'axe de rotation sur un axe qui ne contient pas le centre de gravité du solide tournant nécessite une force compensatrice imposant la rotation de ce centre autour de l'axe, qui entraîne donc un effort périodique sur les paliers, se traduisant en particulier par une vibration induite par le mécanisme en rotation. Cet équilibrage n'est pas toujours possible si la vitesse de rotation doit être très élevée : à mille tours par seconde, un écart de 25 µm entre le centre de gravité et l'axe de rotation créé une force centrifuge tournante de dix fois le poids du rotor[2].

Déséquilibre dynamique d'un arbre.

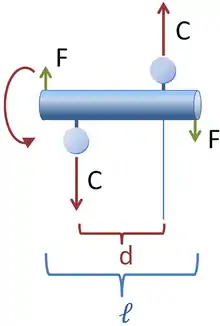
Après avoir ramené le centre de gravité sur l'axe, le deuxième équilibrage est plus subtil, et implique le théorème du moment cinétique. Lorsque la roue tourne, elle a un certain moment cinétique, qui se déduit de sa vitesse de rotation par le moment d'inertie du système physique en rotation. Mais la roue n'est pas toujours parfaitement symétrique par rapport à son axe, et le moment d'inertie du système en rotation est dans le cas général un tenseur d'inertie, ce qui implique que dans le cas général, le vecteur moment cinétique n’est pas colinéaire avec le vecteur vitesse de rotation, c'est-à-dire qu'il n'est pas sur l'axe de rotation.

Le moment d'inertie dépend de la répartition des masses dans le système tournant, et est donc lié à ce système. Quand la roue va tourner suivant un axe fixe, le moment cinétique désaxé tournera avec le système. Quand le théorème du moment cinétique indique que la dérivée temporelle du moment cinétique est égale au moment des forces appliquées, il faut alors prendre ce théorème dans l'autre sens, et dire que puisque le moment cinétique tourne, c'est qu'un moment est appliqué au système, qui compense le fait que l'axe de rotation a été imposé par les paliers. Ce moment, qui est donc proportionnel à la vitesse de rotation, correspond à des forces compensatoires que l'axe de rotation fait subir aux paliers[note 1].

Un arbre peut entrer en résonance si sa vitesse de rotation égale sa fréquence propre.

La rotation de pièces mécaniques peut également concerner des pièces longilignes, comme des arbres, ou comme les ultracentrifugeuses utilisées pour l'enrichissement isotopique[2]. Dans ce cas, le rotor couplé à ses paliers de fixation[3] présente des modes propres de flexion dont la fréquence peut être faible, de l'ordre de grandeur de la vitesse de rotation exprimée en tours par seconde.

Le rotor comporte toujours un certain balourd résiduel, qui entraîne un effort périodique des paliers lors de sa rotation, la fréquence F de cette excitation se déduisant directement de la vitesse de rotation ω. Pour certaines vitesses de rotation, cette fréquence peut coïncider avec celle des modes propres du rotor. Si l'amortissement de tels modes est insuffisant, le rotor peut alors entrer en résonance, ce qui peut entraîner une déformation de grande amplitude, et donc des efforts mécaniques anormaux sur l'arbre et les paliers pouvant entraîner leur destruction.

Ce problème de résonance peut imposer une vitesse limite à la rotation de l'arbre. Dans certains cas, cependant, comme pour les turbo-alternateurs à grande vitesse, il est nécessaire de faire fonctionner l'arbre au-delà de sa première vitesse critique[4], ce qui impose de franchir suffisamment rapidement cette vitesse critique pour que l'amplitude de la résonance reste limitée.

Le volant d'inertie permet de régulariser le couple d'un moteur.

Le mouvement de rotation d'un solide est un mouvement, et il implique par conséquent une énergie cinétique. Dans le cas d'un mouvement de translation, l'énergie cinétique d'un point de masse m est donnée par la formule ${\displaystyle \scriptstyle E_{k}={\frac {1}{2}}mv^{2}}$. Dans le cas d'une rotation d'un solide autour d'un axe fixe, il est possible de montrer l'énergie cinétique totale se met sous la forme ${\displaystyle \scriptstyle E_{k}={\frac {1}{2}}I_{\Delta }.\omega ^{2}}$, où le terme ${\displaystyle \scriptstyle I_{\Delta }}$ est le moment d'inertie par rapport à l'axe de rotation. Le moment d'inertie par rapport à un axe de rotation d'un système solide de points matériels est par définition la somme des masses multipliées par le carré de la distance à l'axe :

${\displaystyle I_{\Delta }=\sum _{i}m_{i}.r_{i}^{2}}$

À poids égal, et à encombrement donné, le moment d'inertie est donc maximal lorsque pratiquement toute la masse est concentrée à distance maximale de l'axe, ce qui est typiquement réalisé par un tore. Le fonctionnement mécanique réel demande que ce tore soit relié à un axe de rotation, par des rayons ou par un disque mince. C'est la forme typique que prend la masse d'un volant d'inertie ou un gyroscope.

Un volant d'inertie est un dispositif mécanique permettant de stocker de l'énergie cinétique sous forme d'énergie de rotation. Un volant typique d'une vingtaine de kilogramme et d'un mètre de rayon aura un moment d'inertie de l'ordre de 20 kg m², et sa mise en rotation à une vitesse relativement faible de un tour par seconde correspond à une énergie de l'ordre de 60 kJ, soit l'énergie nécessaire pour soulever la même masse sur une hauteur de trois mètres. Et si on multiplie cette vitesse par dix, l'énergie stockée est alors multipliée par cent.

Cette énergie peut être restituée si la charge le nécessite, ou s'il faut prendre le relai d'un couple moteur irrégulier. La variation de vitesse de rotation correspondant à la fourniture d'une énergie donnée est alors d'autant plus faible que la vitesse de rotation est importante. En effet :

${\displaystyle \mathrm {d} E_{k}=I_{\Delta }.\omega .\mathrm {d} \omega \qquad }$ et donc ${\displaystyle \quad {\mathrm {d} \omega \over \mathrm {d} E_{k}}=(I_{\Delta }.\omega )^{-1}}$

L'effet d'un volant d'inertie est donc de lisser le fonctionnement lorsque le moteur ou la charge présentent de fortes irrégularités. La rotation sera donc d'autant plus stable que le moment cinétique ${\displaystyle \scriptstyle I_{\Delta }.\omega }$ du système sera grand. Un volant d'inertie est cependant limité dans sa vitesse de rotation par la résistance du matériau dont il est constitué : une vitesse excessive peut conduire à son éclatement, et à la projection de fragments particulièrement meurtriers.

Un cerceau est stabilisé par effet gyroscopique.

Comme signalé ci-dessus, la variation temporelle du moment cinétique est égale au moment global des forces appliquées au système en rotation. Lorsque ce moment appliqué est orthogonal au moment cinétique, ce qui est typiquement le cas de l'effort transmis par un axe sur un volant, il n'a pas d'effet sur la norme du moment cinétique, mais uniquement sur sa direction. Un rapide calcul montre que le moment cinétique L tourne alors dans la direction du moment M dans un mouvement appelé précession, à une vitesse de rotation Ω donnée par :

${\displaystyle \Omega ={M \over L}}$

Mais comme le montre l'exemple du volant d'inertie, un moment cinétique peut prendre des valeurs importantes si la vitesse de rotation du système physique est grande. Dans ce cas, plus le moment cinétique sera grand, et plus il sera stable par rapport à de petites fluctuations des forces extérieures au système.

C'est essentiellement cet effet qui stabilise un cerceau par rapport aux irrégularités de la route, d'autant mieux qu'il roule plus vite. C'est également l'effet utilisé pour stabiliser l'attitude d'un système physique avec un gyroscope.

La dérivée temporelle du moment cinétique (bleu) est le moment (rouge) créé par le porte-à-faux du poids (vert).

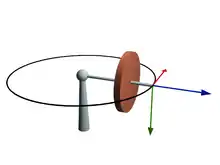
Au-delà de la stabilisation en direction, l'effet le plus spectaculaire d'une rotation rapide d'un volant est celui de la précession d'un gyroscope.

Un gyroscope en rotation rapide a un moment cinétique ${\displaystyle \scriptstyle {\overset {\hookrightarrow }{L}}}$ important et dirigé suivant son axe. Lorsqu'il est placé en porte-à-faux, son poids combiné à la réaction du support forment un couple (physique), dont le moment ${\displaystyle \scriptstyle {\overset {\hookrightarrow }{\mathcal {M}}}}$ est toujours horizontal et perpendiculaire à l'axe. Le théorème du moment cinétique dit que la dérivée du moment cinétique est égale au couple :

${\displaystyle {\overset {\hookrightarrow }{\mathcal {M}}}={\mathrm {d} \over \mathrm {d} t}({\overset {\hookrightarrow }{L}})}$

Ici, l'effet du couple est simplement de faire tourner le moment cinétique suivant un axe de précession vertical, c'est-à-dire sans faire varier l'angle que l'axe de rotation du gyroscope fait par rapport à l'horizontal — ce qui est évidemment paradoxal.

Angles d'Euler de la rotation de la terre : rotation propre(vert), précession (bleu) et nutation (rouge).

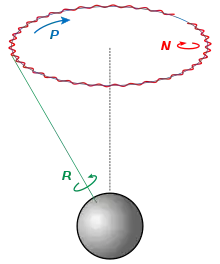
C'est le même effet de précession gyroscopique qui explique la précession des équinoxes, qui fait que l'axe de rotation de la terre tourne autour de l'axe de l'orbite terrestre, mais les forces en cause sont beaucoup moins visibles.

Tout d'abord, lorsque la Terre orbite autour du Soleil, elle est soumise à des forces de marée. Dans un référentiel lié au centre de la terre, en effet, l'attraction solaire (en 1/d²) est équilibrée par la force centrifuge (en ωd²), mais l'équilibre n'est exact que sur l'orbite terrestre. Les points plus proches du Soleil ont un excès d'attraction, qui tend à les rapprocher encore, et les points plus éloignés ont au contraire une attraction déficitaire qui tend à les éloigner. Globalement, donc, un corps en orbite autour du Soleil est soumis à un système de forces qui tend à l'étirer en direction de celui-ci.

Ensuite, la Terre étant en rotation sur elle-même, un point situé sur son équateur subit une force centrifuge qui tend à l'éloigner du centre de la Terre, alors qu'une telle force est absente au pôle. La surface équipotentielle terrestre n'est donc pas sphérique, mais tend à être (très légèrement) aplatie et présente un bourrelet équatorial.

Enfin, l'axe de rotation de la Terre n'est pas perpendiculaire à son orbite (le plan de l'écliptique, mais présente un décalage de 23,45°. De ce fait, lorsque la Terre se présente inclinée par rapport au Soleil, le bourrelet équatorial est soumis au système de forces ci-dessus, qui entraîne un moment parallèle à l'orbite terrestre.

En moyenne annuelle, ce moment est perpendiculaire au moment cinétique terrestre, et lui impose donc une (très lente) rotation. L'axe de rotation terrestre tourne donc lentement, ce qui a pour effet de déplacer la direction du pôle céleste et de l'équateur terrestre (qui lui est perpendiculaire) par rapport au plan de l'écliptique, et donc de faire varier lentement la direction du point vernal, dont le franchissement par le Soleil marque l'équinoxe : c'est ce phénomène que l'on appelle la précession des équinoxes.

Une toupie en rotation.

La toupie est un jouet d'enfant, qui présente dans son mouvement de rotation un comportement un peu plus complexe que le gyroscope et sa « simple » précession. La toupie la plus simple comporte une tige permettant de la mettre en rotation rapide d'un claquement de doigts. Des formules plus complexes comportent une ficelle de lancement, qui permet d'atteindre des vitesses plus rapides, et donc, des comportements prolongés plus intéressants.

Au lancement, la toupie n'est jamais exactement verticale, et montre alors un mouvement de précession identique à celui du gyroscope. Cependant, la « pointe » sur laquelle repose la toupie n'est pas parfaitement pointue mais est plutôt assimilable à une petite sphère, dont le centre est situé près de la pointe. De ce fait, si la toupie est inclinée, son point de contact avec le sol n'est pas situé sur l'axe de rotation. Ce décalage fait que le point de contact glisse et entraîne une force de frottement horizontale, perpendiculaire au plan d'inclinaison de la toupie.

Le moment de cette force par rapport au centre de gravité de la toupie est alors perpendiculaire à son axe de rotation, et une analyse soignée du sens respectif des moments de cette force par rapport au moment d'inertie de la toupie montre que l'effort est dirigé de manière à redresser l'axe de rotation vers la direction verticale. Le système physique se redresse alors pour tourner verticalement sur sa pointe[note 2].

Une fois redressée, la toupie à tige verticale présente un autre comportement intéressant, lorsque sa tige est mise en contact avec un guide, par exemple une règle en bois. L'effet du contact sur la dynamique de la toupie est complexe, et peut se décomposer ainsi :

• La force appliquée par la règle sur la tige est une force qui tend a priori à l'éloigner, mais le moment de cette force tend également à la faire basculer la toupie vers l'avant.
• Le léger basculement de la toupie entraîne un effet de précession, qui tend à ramener la tige sur la règle.
• Le plaquage sur la règle de la tige en rotation provoque une force de frottement dirigée vers l'avant. La force de frottement pousse la toupie à se déplacer vers l'avant, et son moment tend également à ramener la tige de sur la règle.

L'effet global est que la toupie en rotation semble attirée par la règle, et la contourne progressivement en roulant dessus.

Principe du gyrocompas.

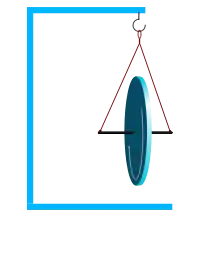
L'effet de frottement peut également être utilisé pour réorienter un gyrocompas sur l'axe de rotation de la Terre. Un gyrocompas est avant tout un gyroscope dont le mouvement est entretenu par un moteur électrique. Si un tel gyroscope est monté sur un cardan bien huilé, qui tourne librement et interdit d'imposer au gyroscope un moment quelconque, le moment cinétique du rotor restera constant y compris dans son orientation dans l'espace. De ce fait, il restera pointé dans la même direction par rapport aux étoiles, et ne sera pas entraîné par la rotation terrestre.

Si au contraire les articulations de la suspension entraînent un frottement, l'effet de ce frottement sera un couple tendant à s'opposer à la rotation terrestre, donc orienté dans la même direction que la rotation terrestre. Ce couple tendra donc à redresser le gyroscope pour l'aligner progressivement sur le nord géographique.

Si le gyrocompas est suspendu de manière que son axe soit horizontal, seule la composante horizontale perpendiculaire à l'axe du moment s'opposant à la rotation terrestre peut avoir un effet, qui est de faire tourner horizontalement cet axe jusqu'à ce que la composante en question soit nulle. Cette suspension impose donc au gyroscope d'orienter son axe vers le nord géographique.

Lorsqu'un système physique est soumis à une rotation d'ensemble, comme l'est un manège forain ou encore la surface de la Terre, il peut être souhaitable d'en repérer les composants par un système de coordonnées attaché au système lui-même. Un point P repéré en coordonnées cylindriques par sa hauteur ${\displaystyle \scriptstyle {\vec {h}}}$ et son rayon ${\displaystyle \scriptstyle {\vec {r}}}$ dans le plan perpendiculaire à l'axe (assimilable au plan complexe) aura alors en réalité comme coordonnées, par rapport à un référentiel galiléen :

${\displaystyle {\overrightarrow {OP}}={\vec {h}}+e^{i\omega t}.{\vec {r}}}$

Si ce point est immobile par rapport au repère en rotation, ${\displaystyle \scriptstyle {\vec {h}}}$ et ${\displaystyle \scriptstyle {\vec {r}}}$ seront constants, et la vitesse et l'accélération de ce point seront donnés par :

${\displaystyle {\vec {v}}={\mathrm {d} \over \mathrm {d} t}({\overrightarrow {OP}})=(i\omega )e^{i\omega t}.{\vec {r}}\qquad }$ et ${\displaystyle \quad {\vec {\gamma }}={\mathrm {d} \over \mathrm {d} t}({\vec {v}})=-\omega ^{2}e^{i\omega t}.{\vec {r}}}$

On retrouve ici le fait qu'un point en mouvement circulaire uniforme à une distance r de son centre de rotation est soumis à une accélération centripète, dirigée vers ce centre de rotation et d'intensité ${\displaystyle \scriptstyle \omega ^{2}r}$. Si ce point matériel est affecté d'une masse, le fait qu'il reste immobile par rapport au système en rotation implique qu'il est soumis d'une manière ou d'une autre à une force centripète qui le maintient en place par rapport à ce repère. Cette force peut avoir n'importe laquelle des origines que l'on peut rencontrer en mécanique statique : tension d'un câble ou d'un ressort, poussée exercée par la pression d'un support, poussée d'Archimède, attraction gravitationnelle, etc.

« L'inclinaison de la moto permet de compenser la force centrifuge », ou « la poussée sur les roues créé une force centripète ».

Pour un observateur lié au repère, ce point qui paraît donc immobile apparaît comme soumis à une force physique réelle, et en même temps paraît immobile dans le repère. Si l'on considère que l'immobilité en mécanique statique traduit l'équilibre des forces en présence, il faut donc ajouter à ces forces physiques réelles une force centrifuge qui ramène le bilan des forces à zéro.

Autrement dit, dans un repère en rotation, il y aura deux manières d'aborder un problème de statique (par rapport au repère) :

• La somme des forces en présence doit être égale à la force centripète nécessaire en ce lieu au point matériel considéré.
• La somme des forces en présence plus une force centrifuge applicable au point matériel en ce lieu est égale à zéro.

Ces deux descriptions sont mathématiquement équivalentes pour l'étude d'un problème « statique », sachant que la force centripète et la force centrifuge sont l'opposée l'une de l'autre.

Centrifugeuse pour l'extraction du miel.

Cependant, les forces physiques présentes dans le bilan sont souvent des forces de réaction, essentiellement dues à l'inertie. Du point de vue de la causalité, il est alors plus naturel de parler d'une force d'inertie causée par la rotation du système et entraînant une réaction du support, que de présenter la réaction du support comme une force « nécessaire pour » faire tourner le point avec son référentiel, ce qui pourrait être compris comme de la téléologie.

Dans une essoreuse à salade (ou un extracteur de miel), la rotation de la manivelle, de l'ordre d'un tour par seconde, est démultipliée six ou sept fois par un engrenage, conduisant à une vitesse de rotation de l'ordre de l'ordre de 40 rad s⁻¹ et une accélération centrifuge de 80 m s⁻² à dix centimètres de l'axe, soit huit fois l'accélération de la pesanteur g. La force centrifuge qui varie comme le carré de la vitesse de rotation peut prendre des valeurs très importantes pour des vitesses de rotation élevées. Dans une ultracentrifugeuse tournant à 15 000 tr min⁻¹, l'accélération centrifuge à dix centimètres de l'axe est de l'ordre de 25 000 g...

Dans une dépression de l'hémisphère nord, les vents aspirés vers le centre sont déviés vers la droite.

Dans un système physique complexe en rotation uniforme, un point P repéré en coordonnées cylindriques par sa hauteur ${\displaystyle \scriptstyle {\vec {h}}}$ et son rayon ${\displaystyle \scriptstyle {\vec {r}}}$ dans le plan perpendiculaire à l'axe (assimilable au plan complexe) aura donc comme coordonnées, par rapport à un référentiel galiléen :

${\displaystyle {\overrightarrow {OP}}={\vec {h}}_{(t)}+e^{i\omega t}.{\vec {r}}_{(t)}}$

Si ce point se déplace par rapport au repère en rotation, ${\displaystyle \scriptstyle {\vec {h}}}$ et ${\displaystyle \scriptstyle {\vec {r}}}$ ne sont plus constants, et la vitesse et l'accélération de ce point seront donnés par :

${\displaystyle {\vec {v}}=\left({\mathrm {d} {\vec {h}} \over \mathrm {d} t}+e^{i\omega t}.{\mathrm {d} {\vec {r}} \over \mathrm {d} t}\right)+(i\omega )e^{i\omega t}.{\vec {r}}\qquad }$ et

${\displaystyle {\vec {\gamma }}=\left({\mathrm {d} ^{2}{\vec {h}} \over \mathrm {d} t^{2}}+e^{i\omega t}.{\mathrm {d} ^{2}{\vec {r}} \over \mathrm {d} t^{2}}\right)+2(i\omega )e^{i\omega t}.{\mathrm {d} {\vec {r}} \over \mathrm {d} t}-\omega ^{2}e^{i\omega t}.{\vec {r}}}$

Si l'on se place dans le repère en rotation pour décrire le mouvement de ce point matériel, on le verra donc apparemment soumis à l'accélération « réelle » représentée par la somme des forces physiques en présence (le premier terme entre parenthèses), à la force centrifuge précédente (le dernier terme), et à une force complémentaire. Cette force complémentaire est, d'une part, perpendiculaire et proportionnelle à la composante de la vitesse perpendiculaire à l'axe, et d'autre part, perpendiculaire et proportionnelle au vecteur rotation. Cette force est donc représentée par le produit vectoriel de la vitesse du point et du vecteur de rotation[note 3] :

${\displaystyle {\overrightarrow {F}}_{C}=-2m{\vec {\omega }}\wedge {\vec {v}}}$

La prise en compte de cette force de Coriolis est importante pour l'étude des trajectoires dans le repère terrestre, parce que la terre a une vitesse de rotation faible (0,729 µrad s⁻¹) mais non négligeable pour des vitesses élevées, ou sur des durées longues. Ainsi, quand une dépression aspire les vents vers son centre, la trajectoire est déviée vers la droite, et le système cyclonique devient principalement une rotation.

Une vitesse de rotation est représentée par une direction et une intensité.

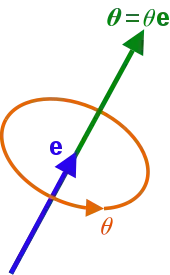
• Voir : Représentation vectorielle d'une rotation (en)

Pour caractériser le mouvement d'un solide en rotation, il faut d'une manière générale trois nombres indépendants. C'est ainsi qu'une rotation peut être représentée par un vecteur ${\displaystyle \scriptstyle {\vec {\omega }}}$, la vitesse de la rotation étant alors la norme du vecteur ${\displaystyle \scriptstyle \omega =||{\vec {\omega }}||}$, et direction de l'axe de rotation étant celle du vecteur unitaire ${\displaystyle \scriptstyle {\vec {u}}={\vec {\omega }}/\omega }$.

La même représentation peut être utilisée pour décrire l'accélération angulaire, qui est simplement la dérivée du précédent vecteur, ainsi que pour représenter l'angle de rotation dont a tourné le système, qui en est au contraire l'intégrale.

On peut remarquer à ce propos que l'angle dont a tourné un système physique, par rapport à une position initiale de référence, n'est connu qu'à un nombre entier de tours près si l'on n'a pas accès à l'historique de la rotation. Il n'est donc pas possible de définir l'écart angulaire par la différence entre la position finale et la position initiale, contrairement au cas de la translation, où le vecteur déplacement peut être ainsi défini.

Cette différence montre bien que l'analogie entre rotation et translation est relativement formelle, et ne se retrouve pas au niveau des grandeurs physiques : dans le cas du mouvement de translation, l'élément fondamental est le déplacement et la vitesse s'en déduit ; dans le cas du mouvement de rotation, l'élément central est au contraire la vitesse de rotation, et l'écart angulaire n'est complètement défini qu'à travers l'intégrale de cette quantité.

Définition des trois angles d'Euler.

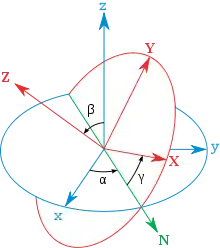
Les angles d'Euler fournissent une méthode alternative pour représenter la position d'un solide par rapport à un référentiel initial, qui est particulièrement bien adaptée à l'étude du mouvement d'un gyroscope.

Par rapport à un référentiel initial défini par les trois axes (x, y, z), les angles d'Euler consistent à faire subir au référentiel trois rotations successives :

• Une première rotation, la précession, fait tourner le repère autour de l'axe vertical z d'un angle α, ce qui amène l'axe x dans une nouvelle direction N (et déplace l'axe y).
• Une deuxième rotation, la nutation, fait tourner le repère autour de cette direction N, pour abaisser l'axe de rotation z d'un angle β, l'amenant sur sa nouvelle position Z (et déplaçant à nouveau l'axe y).
• Enfin, la troisième rotation, la rotation propre, correspond au mouvement de rotation du solide, dont l'axe instantané de rotation a été aligné sur Z. Cette rotation d'un angle γ amène l'axe N sur sa nouvelle position X (et déplace encore une fois l'axe y).

On voit que les deux premières rotations (la précession et la nutation) décrivent l'orientation de l'axe de rotation du système, alors que le troisième angle décrit la rotation proprement dite. On voit d'autre part que ces angles décrivent bien le mouvement du gyroscope : la précession se traduit par une vitesse constante de la précession, et les petites oscillations de l'axe par rapport à ce mouvement moyen se traduisent simplement par des écarts périodiques formant un mouvement circulaire entre la précession et la nutation.

Contrairement à la représentation précédente, où le vecteur pouvait représenter une vitesse angulaire, les trois nombres d'Euler sont des angles ; la vitesse de rotation étant la dérivée du troisième angle par rapport au temps.

Dans le cas simple d'une rotation dans le plan autour de l'origine, il est possible de représenter un point P du plan de coordonnées (a, b) par un nombre complexe z_P = a + ib, et une rotation d'angle α par un nombre complexe z de norme unité :

${\displaystyle z_{\alpha }=\cos(\alpha )+i.\sin(\alpha )=e^{i\alpha }}$

La rotation du point P se représente alors simplement par la multiplication du complexe z_P représentant le point par le complexe z_α représentant la rotation.

Les quaternions sont une extension des nombres complexes, pour lesquels au lieu d'une seule unité imaginaire i on définit trois unités (i, j, k) telles que :

${\displaystyle i^{2}=j^{2}=k^{2}=ijk=-1}$

Les quaternions forment donc des nombres complexes dont la partie imaginaire est de dimension trois. Ces quaternions s'ajoutent et se multiplient comme d'autres nombres (associativité de la multiplication et de l'addition, distributivité de la multiplication sur l'addition, etc), en prenant garde cependant à ce que la multiplication n'est généralement pas commutative : elle est anticommutative si le résultat est imaginaire (ij = -ji), et commutative pour un facteur réel. Par ailleurs, ces trois unités définissent avec l'axe réel un espace à quatre dimensions.

Les quaternions permettent d'encoder simplement les rotations, et d'en combiner les effets. Une rotation est généralement définie par son angle θ et son sens défini par un vecteur unitaire ${\displaystyle \scriptstyle {\vec {u}}}$ de coordonnées (x, y, z). Cette rotation peut alors être représentée par un quaternion généralisant la formule d'Euler :

${\displaystyle {\vec {q}}=e^{{\frac {\theta }{2}}(x.i+y.j+z.k)}=\cos {\frac {\theta }{2}}+(x.i+y.j+z.k)\sin {\frac {\theta }{2}}}$

Avec cette représentation, on montre alors que si l'on encode un vecteur ${\displaystyle \scriptstyle {\vec {P}}}$ de coordonnées (a, b, c) par le quaternion sans partie réelle a.i + b.j + c.k, le quaternion représentant l'image ${\displaystyle \scriptstyle {\vec {P}}'}$ d'un vecteur ${\displaystyle \scriptstyle {\vec {P}}}$ par une rotation d'angle θ et de direction ${\displaystyle \scriptstyle {\vec {u}}}$ est donné par :

${\displaystyle P'={\vec {q}}.P.{\vec {q}}^{-1}}$

Grâce à cette identité, les opérations sur les combinaisons de rotations peuvent se traduire par des opérations algébriques équivalentes sur les quaternions, la composée de deux rotation étant le produit des quaternions associés.

• Mouvement de rotation
• Rotation vectorielle
• Cerceau
• Disque d'Euler
• Toupie (jouet)
• Gyroscope
• Anagyre (objet)
• Boomerang