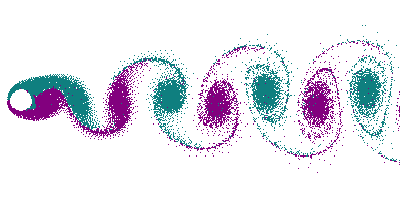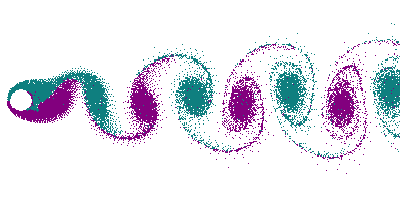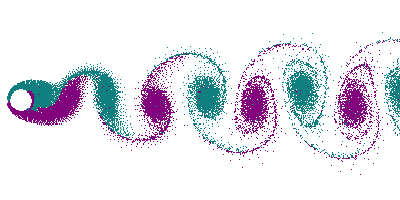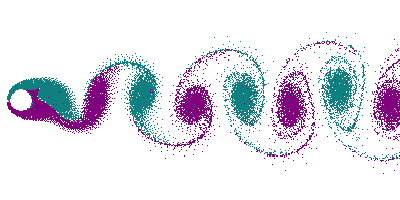Mécanique des fluides

L'hydrostatique, ou statique des fluides, est l'étude des fluides immobiles. Ce domaine a de nombreuses applications comme la mesure de pression et de masse volumique. Elle offre des explications physiques à de nombreux phénomènes de la vie quotidienne, comme la poussée d’Archimède ou les raisons pour lesquelles la pression atmosphérique change avec l'altitude.

L'hydrostatique est fondamentale pour l'hydraulique, l'ingénierie des équipements de stockage, de transport et d'utilisation des fluides. Elle est également pertinente pour certains aspects de la géophysique ou de l'astrophysique (par exemple, pour comprendre la tectonique des plaques et les anomalies du champ gravitationnel de la Terre), pour la météorologie, la médecine (dans le contexte de la pression artérielle) et de nombreux autres domaines.

La dynamique des fluides, ou hydrodynamique, est une sous-discipline de la mécanique des fluides qui traite de l'écoulement des fluides, soit les liquides ou les gaz en mouvement[1]. La dynamique des fluides offre une structure systématique qui englobe des lois empiriques et semi-empiriques, dérivées de la mesure du débit et utilisées pour résoudre des problèmes pratiques. La solution à un problème de dynamique des fluides implique généralement le calcul de diverses propriétés du fluide, telles que la vitesse, la pression, la densité et la température, en tant que fonctions de l'espace et du temps.

La dynamique des fluides couvre plusieurs sous-disciplines comme :

• l'aérodynamique[2] - [3] - [4] - [5] (l'étude des gaz en mouvement) ;
• l'hydrodynamique[6] - [7] (l'étude des liquides en mouvement).

Mesures, dans l'air, des caractéristiques hydrodynamiques d'un sous-marin dans la soufflerie Full-scale de Langley.

Distribution des pressions sur des ogives ellipsoïdales de fusées (en subsonique) d'après les mesures en tunnel hydraulique de Rouse et McNown.

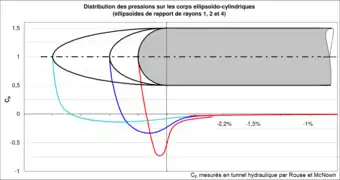
S'agissant d'écoulements de gaz incompressibles (ou assimilés), l'aérodynamique rejoint précisément l'hydrodynamique (et vice-versa), c'est-à-dire que les raisonnements théoriques et les mesures expérimentales qui valent pour les liquides valent aussi pour les gaz (incompressibles ou assimilés) et vice et versa. Ainsi peut-on calculer théoriquement avec les mêmes méthodes les efforts suscités par des écoulements liquides ou gazeux (incompressibles ou assimilés) ; ainsi encore peut-on déterminer expérimentalement les caractéristiques de portance et de traînée de fusées dans l'eau (image de gauche) ou de sous-marins dans l'air (image de droite).

La dynamique des fluides a un large éventail d'applications, dont le calcul des forces et moments s'appliquant sur les aéronefs, la détermination du débit massique de pétrole dans les pipelines, la prévision de l'évolution des conditions météorologiques, la compréhension des nébuleuses dans l'espace interstellaire et la modélisation des explosions. Certains principes de dynamique des fluides sont utilisés dans l'ingénierie du trafic et la dynamique des foules.

Au niveau le plus bas de la modélisation, on décrit le milieu par position et vitesse de chaque particule constitutive et le potentiel d'interaction entre elles. Cette approche est bien sûr limitée par la quantité d'information qu'elle suppose. Elle est utilisée :

• en pratique dans les méthodes de dynamique moléculaire où elle constitue une véritable expérience numérique possible pour un liquide comme pour un gaz,
• en théorie pour des tentatives de construction ab initio d'un système formel de description macroscopique du milieu. Ce type d'approche est extrêmement difficile et peu de résultats ont été obtenus depuis les travaux de Jean Leray. En particulier, l'existence de solutions régulières des équations de Navier-Stokes fait l'objet du prix Clay.

Pour les gaz et à un niveau moins détaillé on se contente de décrire la distribution statistique des vitesses et éventuellement de tous les autres degrés de liberté (énergie interne, rotation et vibration dans le cas de molécules). Ludwig Boltzmann a ainsi réussi à écrire l'équation cinétique qui porte son nom. Cette fonction du temps, de la position et de la vitesse peut être calculée à partir d'outils comme la simulation directe Monte Carlo ou la méthode de gaz sur réseau particulièrement bien adaptée aux milieux poreux. Il s'agit de calculs coûteux en raison de la dimension 7 du problème. Pour cette raison on utilise généralement un potentiel d'interaction peu réaliste physiquement mais conduisant à des résultats acceptables.

Par ce vocable on entend la description de phénomènes descriptibles à une échelle grande devant la précédente mais petite devant l'échelle du continu.

La particule fluide décrit un fluide à l'échelle mésoscopique : c'est un volume de dimension suffisamment petite pour que les propriétés du fluide ne varient pas spatialement dans la particule et suffisamment grand pour qu'une quantité importante de molécules soient comprises dedans de manière à moyenner les fluctuations statistiques[8].

On peut effectuer dans cette particule un bilan de masse, de quantité de mouvement et d'énergie en utilisant les flux correspondants sur les limites du domaine. Cette approche conduit à l'écriture des équations de conservation correspondantes et, par passage à la limite, aux équations descriptives du phénomène. Cette méthode est aussi la base de la description numérique, le volume élémentaire étant alors la maille élémentaire du calcul.

La géométrie étudiée peut comprendre des détails dont la prise en compte explicite va rendre le problème coûteux, par exemple une rugosité de la surface ou le détail de la géométrie d'un milieu poreux. Dans ce dernier cas les méthodes bien connues de la prise de moyenne volumique ou de l'homogénéisation permettent le calcul de quantités intervenant sous forme de coefficients comme le coefficient de diffusion dans l'équation de Darcy. Dans le cas d'une rugosité l'homogénéisation aboutit à l'écriture d'une relation de saut à la paroi, c'est-à-dire une relation liant toute valeur à sa dérivée spatiale.

On peut faire également entrer dans cette catégorie les phénomènes de raréfaction dans un choc ou une couche pariétale. Dans ces régions d'espace les équations du continu sont invalides sur une distance de quelques libres parcours moyens. On peut généralement les ignorer. Lorsque ce n'est pas les cas leur modélisation aboutit comme précédemment à des équations de saut. Les relations de Rankine-Hugoniot en sont un exemple.

Enfin, et ce n'est pas le moindre problème, on peut faire disparaître toutes les fluctuations d'un écoulement turbulent par des méthodes de moyennage très diverses, pouvant ramener le problème à une simple diffusion équivalente. Là aussi le but est de simplifier le calcul, possible par la simulation directe, mais coûteux.

Le niveau macroscopique résulte donc d'une simplification drastique de tous les détails du problème, lesquels sont tout de même présents au travers des coefficients qui interviennent dans les équations descriptives, des conditions aux limites et de l'équation d'état du milieu.

Ces notions qui séparent nettement deux types d'écoulements ont une origine microscopique :

• le caractère compressible généralement associé à un gaz est lié au fait qu'un tel milieu est formé d'objets très espacés ayant des interactions rares, caractérisées par un potentiel particule-particule. Ceci est vrai même dans le cas de milieux contenant des espèces chargées en faible proportion, où les électrons ne sont pas totalement libres et accompagnent (statistiquement) les ions (diffusion ambipolaire). La connaissance de ces potentiels, aujourd'hui d'origine spectroscopique[alpha 1], est suffisante pour permettre le calcul de toutes les propriétés de transport du milieu : coefficients de diffusion binaire et thermique (équations de Stefan-Maxwell), viscosités dynamique et volumique, conductivité. Ce caractère de milieu peu dense n'est pas affecté par un changement de pression donc une variation du libre parcours moyen entre deux collisions.
• le caractère d'incompressibilité associé aux liquides est lié aux liaisons que voit une particule dans un tel milieu. Elle est en effet liée à plusieurs voisins, même si ces liaisons ne sont pas aussi strictes que dans un solide. Ce caractère interdit une approche formelle comme dans les gaz : les propriétés de transport sont mesurées, la théorie ne permettant que d'expliquer les variations avec la température par exemple[9]. L'incompressibilité des liquides n'est cependant pas absolue : une pression très élevée de quelques centaines de GPa telle que rencontrée dans le noyau terrestre met en évidence une variation de masse volumique des composants liquides.
• Dans la pratique, pourtant, on peut souvent considérer les gaz comme incompressibles, du moins lorsqu'ils s'écoulent à un nombre de Mach inférieur à 0,4 (ou plus, selon la précision requise). Cette licence d'ingénieur ne signifie pas que, dans ces circonstances, les gaz soient vraiment incompressibles (ils sont compressibles) mais elle vaut parce que leur compressibilité modifie assez peu les conditions de calcul de leur écoulement (et des forces qui vont avec, pour l'ingénieur).

On peut obtenir ces équations par au moins deux voies :

• à partir des relations de conservation de la masse, de la quantité de mouvement et de l'énergie,
• à partir de l'équation de Boltzmann décrivant l'évolution moléculaire par la méthode de Chapman-Enskog. Cette méthode n'est utilisable que pour les gaz en raison de la simplicité relative des interactions au niveau microscopique dans ce cas.

Dans la première méthode apparaissent le tenseur des contraintes (ou tenseur de pression, incluant contraintes visqueuses et pression) et le flux de chaleur. Pour ces deux quantités on fait l'hypothèse qu'elles sont liées à un gradient :

• le flux de chaleur est proportionnel au gradient de température (loi de Fourier),
• le tenseur des contraintes est proportionnel au tenseur des vitesses de déformation (hypothèse de Stokes). En une dimension d'espace cette expression s'exprime en disant que la contrainte visqueuse est proportionnelle au taux de cisaillement. Ceci définit un écoulement « newtonien ».

Le mécanisme sous-jacent dans les deux cas n'est pas très apparent : on se doute que cette proportionnalité est liée à une linéarisation des équations qui décrivent le problème exact sous-jacent. C'est là un processus général en physique mathématique.

La méthode partant du microscopique permet d'éclairer cet aspect. Les équations de Navier-Stokes sont l'expression d'une petite perturbation de la fonction de distribution microscopique des vitesses et, éventuellement, des énergies internes (statistique de Maxwell-Boltzmann). A contrario les équations d'Euler décrivent le cas correspondant à l'équilibre thermodynamique local.

Il faut alors donner les coefficients qui interviennent : pression, viscosité et conductivité. La pression est définie par l'équation d'état. Les propriétés de transport, viscosité et conductivité peuvent résulter dans le cas du gaz d'un calcul effectué à partir du niveau microscopique (du potentiel interatomique). Pour les liquides ces quantités relèvent de l'expérience.

La similitude est la mise en évidence de nombres sans dimensions permettant de réduire le nombre de paramètres intervenant dans les équations afin de simplifier son analyse, éventuellement de définir des expériences à l'échelle du laboratoire. Elle est basée sur l'invariance d'échelle qui assure la covariance des équations : celles-ci sont valides dans tout référentiel galiléen.

On peut alors par un changement de variable faire apparaître des nombres adimensionnels et diminuer ainsi le nombre de variables d'un problème.

Instabilité de Kelvin-Helmholtz matérialisée par des nuages.

L'instabilité des solutions des équations est due au terme non linéaire de transport de quantité de mouvement V ⋅ ∇V. Elles correspondent à une bifurcation de la solution obtenue pour une certaine valeur du nombre de Reynolds. On rencontre divers types d'instabilités :

• instabilité de cisaillement bidimensionnelle pour des profils de vitesse perpendiculaire à l'écoulement ayant un point d'inflexion (instabilité de Kelvin-Helmholtz). Le tourbillon généré est dans le plan de l'écoulement ;
• instabilités centrifuges de type Taylor-Couette qui se crée lorsque le moment cinétique r V(r) décroît lorsque l'on s’éloigne du centre de courbure. Le tourbillon généré est perpendiculaire à l'écoulement, conduisant par exemple aux tourbillons de Görtler. Il existe nombre d'autres instabilités de type inertiel telles les instabilité elliptique et instabilité de Crow rencontrées en aéronautique ou en géophysique[10].

De plus les interfaces soumises à une accélération ou à un champ de gravité peuvent être le siège d'instabilités : Rayleigh-Taylor, Richtmyer-Meshkov, etc.

Strioscopie de l'écoulement transitionnel créé par une chandelle.

Le passage de l'état laminaire d'un écoulement vers un état totalement turbulent peut emprunter plusieurs voies :

• transition naturelle : une perturbation quelconque est amplifiée comme le montre une analyse de stabilité (équation de Orr-Sommerfeld). Les perturbations d'abord régulières (ondes de Tollmien-Schlichting) se déforment, créent des tourbillons longitudinaux qui sont eux-mêmes déformés et qui finissent par créer des régions (« spots ») turbulentes, lesquelles finissent par occuper tout l'espace.
• transition « by-pass » : ce phénomène, présent dans les couches limites, désigne une transition forcée par la contamination par une turbulence externe. Les premières étapes de la transition naturelle sont contournées, d'où le nom.
• transition par rugosité : les irrégularités de la paroi sont un moteur puissant de déstabilisation de la couche limite.
• transition par décollement de l'écoulement moyen créant une couche de cisaillement instable.

Il n'existe pas de modèle universel de transition. Ceci est aisément compréhensible dans le cas de la transition naturelle où la source de l'instabilité peut être diverse et où de plus son amplitude joue un rôle. De même on ne maîtrise pas forcément une turbulence externe. En pratique on utilise des critères expérimentaux valides sur telle ou telle configuration.

Visualisation par fluorescence induite par laser d'un jet turbulent.

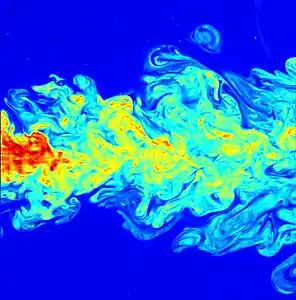
La turbulence est un phénomène étudié depuis Léonard de Vinci mais encore mal compris. Il n'existe pas de théorie permettant de décrire le phénomène à partir des équations de Navier-Stokes. La cascade turbulente se manifeste par un transfert d'énergie des grandes structures créées par les gradients de vitesse - encore le terme V ⋅ ∇V - vers les petits tourbillons détruits par dissipation visqueuse. Un résultat majeur obtenu par Kolmogorov est la description des échelles intermédiaires où se produit une diffusion de l'énergie cinétique par mélange et étirement/repli des tourbillons. Cette région possède une propriété d'auto-similitude : les transferts se produisent identiquement à toutes les échelles. Ce résultat illustre la capacité explicative de l'approche physique statistique et systèmes dynamiques.

Une turbulence quasi-bidimensionnelle est obtenue lorsque l'une des dimensions du problème est limitée. C'est le cas de l'atmosphère, où les grands tourbillons excèdent largement la « hauteur utile » où peut se développer une troisième dimension. Il se produit alors une double cascade d'énergie[11].

En pratique, l'approche physique statistique ne permet pas un calcul global. De même la résolution directe des équations est beaucoup trop coûteuse et ne sert qu'à générer des expériences numériques servant de test à une théorie. En pratique la mécanique des fluides numérique utilise une méthode où les moments des corrélations statistiques des variables issus d'une prise de moyenne sont modélisés par une hypothèse physique raisonnable. Il existe plusieurs modèles, chacun étant plus ou moins adaptée à une situation donnée.

Les effets de la turbulence sur l'écoulement sont importants. Directement ils favorisent les échanges de masse, quantité de mouvement et énergie. Ce phénomène augmente également le bruit acoustique. Il a aussi un effet indirect en modifiant la structure globale d'une région, par exemple la région décollée d'une couche limite ou un jet.

Pour beaucoup de fluides, le tenseur des contraintes peut s'écrire comme la somme d'un terme isotrope (la pression p) et d'un déviateur (le cisaillement):

${\displaystyle \sigma _{ij}=\underbrace {-p\,\delta _{ij}} _{pression}+\underbrace {\mu \left({\frac {\partial V_{i}}{\partial x_{j}}}+{\frac {\partial V_{j}}{\partial x_{i}}}\right)} _{cisaillement}}$

δ_ij est le symbole de Kronecker, μ la viscosité dynamique et V la vitesse.

En réalité, il existe toujours un terme de viscosité volumique μ' div V δ_ij correspondant à une variation isotrope de volume et dû à des interactions moléculaires inélastiques. Ce terme est généralement négligé quoique mesurable et, dans le cas des gaz, calculable[12]. Très petit, il est supposé nul dans l'hypothèse de Stokes.

Certains matériaux comme les verres ont un comportement qui passe continûment de l'état solide à l'état liquide. C'est vraisemblablement le cas du verre commun si l'on en croit les mesures de viscosité dans la plage où celles-ci sont faisables en un temps raisonnable[13] - [alpha 2] ou celle du Silly Putty.

Versement vertical d'un shampooing qui crée un jet latéral par effet Kaye.

De nombreux fluides ont des comportements différents, particulièrement en cisaillement. Ce comportement est lié à leur composition : phase solide en suspension, polymère, etc. Leur étude relève de la rhéologie. On présente généralement leur comportement sous un cisaillement simple pour lequel la viscosité est la pente de la courbe contrainte-déformation :

• le fluide de Bingham (boue de forage, dentifrice) qui a un comportement visqueux newtonien passé un seuil de déformation correspondant à la dislocation de sa structure au repos.
• fluides rhéofluidifiants ou pseudo-plastiques (sang, peintures, pâte à papier, etc.) dont la viscosité apparente diminue avec la contrainte appliquée, le phénomène étant lié à une diminution des liaisons internes, affectées par l'écoulement. Certains fluides de Bingham ont un comportement pseudo-plastique.
• à l'inverse certains fluides sont rhéoépaississants ou dilatants comme les suspensions concentrées.

La relation contraintes-déformation n'est pas suffisante pour caractériser certains fluides dont le comportement est plus complexe :

• dépendance en fonction du temps comme les fluides thixotropes comme le ketchup dont la viscosité apparente diminue avec le temps sous contrainte constante. Ce phénomène est lié à une déstructuration plus ou moins rapide du milieu. Plus rarement on rencontre des fluides antithixotropes comme le latex.
• Un autre caractère possible est l'élasticité de fluides comme certaines résines polyacrilamides capables d'aligner leurs chaînes macromoléculaires dans le sens de l'écoulement.

Ces caractéristiques peuvent donner naissance à des comportements remarquables comme :

• l'effet Weissenberg pour les fluides pseudo-plastiques[14] ;
• l'effet de siphon ouvert pour les fluides élastiques[15] ;
• l'effet Kaye pour les fluides thixotropes[16].

Les comportements peuvent être décrits par des modèles rhéologiques obtenus en ordonnant de manière plus ou moins complexes des éléments de base : ressort pour l'élasticité, amortisseur pour le comportement visqueux, patin pour la pseudo-plasticité[17]. On obtient ainsi le modèle de Kelvin-Voigt ou le modèle de Maxwell pour décrire la viscoélasticité.

Les caractéristiques sont mesurées à l'aide de rhéomètres ou, dans le cas des polymères, peuvent être prédites[18].

Allée de tourbillons de Karman.

Un écoulement peut être stationnaire ou instationnaire ou les deux à la fois. Prenons l'exemple de l'écoulement autour d'un cylindre infini[19] :

• à bas nombre de Reynolds basé sur le diamètre l'écoulement est laminaire et stationnaire ;
• lorsque le nombre de Reynolds augmente (Re ≈ 10), on voit apparaître une région de recirculation à l'arrière : cet écoulement est stationnaire ;
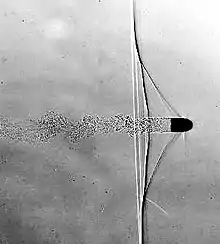
• cette recirculation entraîne une instabilité de type Kelvin-Helmholtz (Re ≈ 100) et l'apparition d'allées de Kármán par appariement des tourbillons produits de part et d'autre[20] - [21] ;
• à plus grand nombre de Reynolds (Re ≈ 1000) l'écoulement de sillage devient turbulent donc instationnaire mais stationnaire en moyenne statistique.

Tourbillon de bout d'aile.

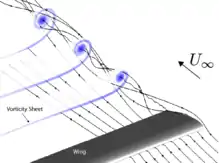
Les tourbillons peuvent naître dans une région décollée comme la recirculation dans l'exemple précédent. Il s'agit alors d'un phénomène entretenu d'origine visqueuse.

Ils peuvent également avoir pour origine une dissymétrie des conditions aux limites : c'est le cas des extrémités d'une aile d'avion. Dans ce cas il s'agit d'un phénomène inertiel non entretenu (en un point de l'espace donné). Les tourbillons ainsi créés sont de grande taille et peu affectés par la viscosité, ce leur confère une grande durée de vie.

Mathématiquement, le tourbillon (ou vorticité) se définit comme le rotationnel de la vitesse ou la moitié de cette valeur. On sait écrire une équation de transport pour cette quantité[22] qui est à la base des études sur la turbulence vue sous l'angle mécanique des fluides et non sous l'angle statistique comme dans l'étude de la cascade turbulente.

Balle de fusil en vol transsonique.

Tous les fluides sont visqueux jusqu'à un certain degré. La compressibilité de l'eau par exemple vaut environ 5 × 10⁻¹⁰ m² N⁻¹, ce qui suppose des pressions de l'ordre du kilobar pour obtenir un effet mesurable. Cette faible valeur permet dans le cas général de faire l'approximation de masse volumique constante. Les écoulements dans lesquels cette approximation est valide sont généralement tels que la température y est sensiblement constante et où l'on peut par suite supposer la viscosité constante. L'équation de conservation de l'énergie est découplée et les équations de Navier-Stokes réduites à une forme plus simple. Si de plus on suppose le nombre de Reynolds petit (Re ≈ 1) on aboutit à l'équation de Stokes. Dans le cas d'un écoulement irrotationnel on montre que la vitesse découle d'un potentiel : on parle d'écoulement potentiel.

Toutefois, la compressibilité d'un liquide n'est jamais nulle et il est possible d'y propager une onde de choc, laquelle suppose une discontinuité des toutes les variables comme indiqué par les relations de Rankine-Hugoniot. Celles-ci sont relatives aux équations d'Euler, donc à un milieu sans viscosité. Cette discontinuité n'existe qu'au point de vue macroscopique puisque la théorie cinétique montre pour les gaz une variation rapide sans discontinuité sur une distance de quelques libres parcours moyens.

L'onde de choc résulte d'une propriété remarquable des équations d'Euler : leur caractère hyperbolique. L'information dans le milieu est transportée par les caractéristiques. Ceci a donné lieu par le passé à des méthodes de résolution par construction géométrique dans des cas assez simples comme une tuyère ou l'onde accompagnant un objet en vol supersonique. Cette propriété est aujourd'hui à la base des méthodes de résolution numérique par volumes finis : les solveurs de Riemann.

Hors problème de turbulence, les effets dits visqueux, en fait tous les effets liés au transport de masse (diffusion), de quantité de mouvement (cisaillement) et d'énergie (conduction), sont généralement confinés à des régions particulières, généralement une paroi et dans ce cas on parle de couche limite. Un immense progrès dans la compréhension de ce phénomène a été fait au début du XX^e siècle. Il a permis l'avènement de l'aérodynamique moderne grâce à l'analyse que permet son caractère parabolique : l'information ne remonte pas l'écoulement. En outre la relative simplicité des équations autorise la mise en évidence de solutions approchées.

La Grande Vague de Kanagawa ou la transition d'un écoulement à surface libre vers un écoulement diphasique

Les écoulements à surface libre désignent les écoulements d'un fluide limité par une surface libre continue. Ils concernent essentiellement l'atmosphère, les océans ou les lacs et les rivières ou canaux, mais peuvent aussi décrire une étoile par exemple.

Les problèmes à grande échelle dans l'atmosphère ou l'océan ne possèdent pas de caractère spécifique. Ils sont décrits par les équations de Navier-Stokes. D'autres sont limités dans une ou plusieurs directions d'espace. Ce sont :

• les écoulements en eau peu profonde qui peuvent se rencontrer dans l'atmosphère. Ils sont décrits par une vitesse où deux composantes sont dominantes. On décrit ainsi les courants de marée, les seiches, les mascarets, les vagues non déferlantes, les ondes de gravité comme le tsunami mais aussi dans l'atmosphère les ondes de Rossby, de Kelvin, etc.
• les écoulements de canaux et rivières qui sont décrits par leur seule vitesse moyenne.

La tension superficielle ne joue pas de rôle dans ce type de problème.

Cavitation générée par une hélice.

Ce domaine de la mécanique des fluides[23] s'intéresse à ce qui se passe lorsque l’on a affaire à plusieurs phases qui s’écoulent ensemble. Dans la majorité des cas il s'agit d'un milieu diphasique où une phase mineure en volume est dispersée dans la phase majeure. On peut distinguer en fonction du milieu majoritaire :

• liquide contenant un gaz sous forme de bulles (ébullition, échangeur de chaleur), de liquide (nombreuses applications industrielles, en particulier l'industrie pétrolière), de solide (suspensions diluées) ou de vide (cavitation),
• gaz contenant un liquide sous forme de gouttes (sprays).

Cette systématisation des phénomènes peut faire illusion : cela cache des problèmes de natures très différentes. Par exemple les bulles et leur interaction avec leur environnement constituent à elles seules un vrai problème physique que l'on doit aborder avant même de s'intéresser au problème diphasique.

Pour le traitement théorique et numérique du problème on distingue les méthodes cinétique où l'on suit chaque élément de la phase diluée en lui appliquant les lois d'interaction ad hoc (par exemple dans l'équation de Mason-Weaver) et méthodes bifluides où des équations de Navier-Stokes couplées sont écrites pour chaque phase, moyennant certaines hypothèses sur le moyennage des phases (exemple de la méthode du volume de fluide. Cette méthode est plus économique mais pose souvent des problèmes de conditions aux limites où les hypothèses ne sont pas respectées.

Il faut noter que les systèmes diphasiques sont susceptibles de montrer des instabilités spécifiques, un exemple remarquable étant le geyser.

En taille et fraction suffisante les éléments dispersés peuvent affecter la turbulence.

Microtomographie d'un composite Ti₂AlC / Al.

Les écoulements en milieu poreux sont présents dans de nombreux domaines comme l'hydrologie, les protections thermiques, etc. Il s'agit souvent de fluides homogènes mais on rencontre des cas hétérogènes comme dans l'extraction pétrolière. Ce sont par nature des écoulements de fluide à faible vitesse, généralement décrits par l'équation de Stokes à l'échelle du pore. La loi de Darcy établie expérimentalement est démontrable par prise de moyenne volumique ou homogénéisation sous cette condition. L'extension à des écoulements plus rapides (loi de Darcy-Forchheimer) se fait en introduisant un nombre de Reynolds. Pour les gaz on sait également traiter tous les régimes d'écoulement depuis le moléculaire jusqu'au continu (équation de Darcy-Klinkenberg).

La quantité importante dans le domaine est la perméabilité. Celle-ci est mesurable. Elle a longtemps été évaluée théoriquement par des modèles utilisant des porosités de forme simple, respectant la porosité (par exemple la loi de Kozeny-Carman). Ces méthodes ont une prédictibilité limitée aux variations et non aux valeurs absolues. Ceci a changé avec l'avènement de la microtomographie qui permet une simulation numérique directe du phénomène à l'échelle du pore.

• Ouvrages généraux
  • Patrick Chassaing, Mécanique des fluides : Élément d'un premier parcours, Éditions Cépaduès, 2010, 533 p. (ISBN 978-2-85428-929-9 et 2-85428-929-3)
  • (en) Lev Landau et Evgueni Lifchits, Mécanique des fluides, Moscou/Paris, Ellipses Marketing, 1989, 592 p. (ISBN 2-7298-9463-2)
  • (en) George K. Batchelor, An Introduction to Fluid Dynamics, Cambridge/New York, Cambridge University Press, 2000, 615 p. (ISBN 0-521-66396-2)
  • (en) Hermann Schlichting et Klaus Gernsten, Boundary Layer Theory, Springer, 1955, 782 p. (ISBN 978-3-662-52917-1, lire en ligne)
• Passage du microscopique au continu
  • (en) Sydney Chapman et Thomas George Cowling, The Mathematical Theory of Non-uniform Gases : an account of the kinetic theory of viscosity, thermal conduction, and diffusion in gases, Cambridge/New York/Port Chester etc., Cambridge University Press, 1991, 422 p. (ISBN 0-521-40844-X)
  • (en) Joseph Oakland Hirschfelder, Charles Francis Curtiss et Robert Byron Bird, Molecular Theory of Gases and Liquids, John Wiley and Sons, 1966 (ISBN 978-0-471-40065-3)
• Turbulence
  • Christophe Bailly et Geneviève Compte-Bellot, Turbulence, CNRS Editions, 2003, 376 p. (ISBN 2-271-06008-7)
  • (en) Stephen B. Pope, Turbulent Flows, Cambridge University Press, 2000, 771 p. (ISBN 978-0-521-59886-6, lire en ligne)
• Loi de comportement
  • (en) Rutherford Aris, Vectors, Tensors, and the Basic Equations of Fluid Mechanics, New York, Dover Publications, 1962, 286 p. (ISBN 0-486-66110-5, lire en ligne)
  • Guy Couarraze, Jean-Louis Grossiord et Nicolas Huang, Initiation à la rhéologie, Éditions Lavoisier, 2014 (ISBN 978-2-7430-1568-8 et 2-7430-1568-3)
  • (en) R. Byron Bird, Robert C. Armstrong et Ole Hassager, Dynamics of Polymeric Liquids : Fluid Dynamics, Wiley Intersciences, 1987 (ISBN 0-471-80245-X)
• Milieux poreux
  • (en) Kambiz Vafai (Ed.), Handbook of Porous Media., CRC Press, 2015, 959 p. (ISBN 978-1-4398-8557-4, lire en ligne)
  • (en) Stephen Whitaker, The Method of Volume Averaging, Kluwer Academic Publishers, 2010, 471 p. (ISBN 978-3-642-05194-4)
• Diphasique
  • (en) George Yadigaroglu and Geoffrey F. Hewitt (Eds.), Introduction to Multiphase Flow, Springer, 2018 (ISBN 978-3-319-58717-2)
  • (en) Christopher Earls Brennen, Cavitation and Bubble Dynamics, New York/Oxford, Oxford University Press, 1995, 282 p. (ISBN 0-19-509409-3, lire en ligne)
  • (en) Dimitri Gidaspow, Multiphase Flow and Fluidization : Continuum and Kinetic Theory Descriptions, Academic Press, 2012, 467 p. (ISBN 978-0-12-282470-8, lire en ligne)
• Écoulements à surface libre
  • Olivier Thual, Des ondes et des fluides : articles pédagogiques multimédia, Toulouse, Cépaduès, 2005, 197 p. (ISBN 2-85428-655-3)
  • (en) Hendrik C. Kuhlmann et Hans-Josef Rath (Eds.), Free Surface Flows, Springer-Verlag, 1998, 331 p. (ISBN 978-3-7091-2598-4, lire en ligne)
  • (en) Geoffrey K. Vallis, Atmospheric and Oceanic Fluid Dynamics, Cambridge University Press, 2017 (ISBN 978-1-107-58841-7)
• Mécanique des fluides numérique
  • (en) Joel H. Ferziger et Milovan Peric, Computational Methods for Fluid Dynamics, Springer-Verlag, 2002, 426 p. (ISBN 978-3-540-42074-3)
  • (en) Klaus A. Hoffmann et Steve T. Chiang, Computational Fluid Dynamics, Engineering Education System, 2000 (ISBN 0-9623731-3-3, lire en ligne)

• Étienne Guyon, Jean-Pierre Hulin et Luc Petit, Ce que disent les fluides : la science des écoulements en images, Paris, Belin, 2005, 159 p. (ISBN 2-7011-3557-5)
• Romain Rioboo, « Introduction à la mécanique des fluides », sur YouTube
• Isabelle Gallagher, « Kolmogorov, le spectre de la turbulence », sur Bibliothèque nationale de France

• Cinématique des fluides (en)
• Ligne de courant
• Estimation stochastique en mécanique des fluides

• Notices d'autorité :

  • BnF (données)
  • LCCN
  • GND
  • Japon
  • Espagne
  • Israël
  • Tchéquie
  • Corée du Sud
• Notices dans des dictionnaires ou encyclopédies généralistes :

  • Britannica
  • Encyclopédie de l'Ukraine moderne
  • Store norske leksikon
  • Universalis