Modèle de Maxwell

Représentation schématique du modèle de Maxwell.

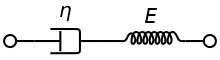
Le modèle de Maxwell est représenté par un amortisseur purement visqueux et un ressort hookéen mis en série comme l'indique le schéma ci-contre. Dans cette configuration, lorsqu'une contrainte axiale est appliquée, la contrainte totale ${\displaystyle {\sigma _{Total}}}$ et la déformation totale ${\displaystyle {\gamma _{Total}}}$ sont définies de la manière suivante :

${\displaystyle {\sigma _{Total}}={\sigma _{A}}={\sigma _{R}}}$

${\displaystyle {\gamma _{Total}}={\gamma _{A}}+{\gamma _{R}}}$

où l'indice A désigne l'amortisseur et l'indice R le ressort.

Les contraintes de l'amortisseur et du ressort sont données respectivement par :

${\displaystyle \sigma _{A}=\eta {\dot {\gamma }}}$

${\displaystyle \sigma _{R}=E\gamma }$

où ${\displaystyle E}$ est le module élastique associé au ressort et ${\displaystyle \eta }$ le coefficient de viscosité associé à l'amortisseur représentant un fluide newtonien.

Dérivons la déformation totale par rapport au temps :

${\displaystyle {\frac {d\gamma _{Total}}{dt}}={\frac {d\gamma _{A}}{dt}}+{\frac {d\gamma _{R}}{dt}}={\frac {\sigma }{\eta }}+{\frac {1}{E}}{\frac {d\sigma }{dt}}}$

En notant la dérivée temporelle par un point, l'équation précédente se réécrit :

${\displaystyle {\frac {\dot {\sigma }}{E}}+{\frac {\sigma }{\eta }}={\dot {\gamma }}}$.

En multipliant cette équation par ${\displaystyle \eta }$,

${\displaystyle \tau {\dot {\sigma }}+\sigma =\eta {\dot {\gamma }}}$

on a fait apparaître le temps de relaxation de Maxwell :

${\displaystyle \tau ={\frac {\eta }{E}}}$.

La solution générale de l'équation de Maxwell s'écrit :

${\displaystyle \sigma (t)={\frac {\eta }{\tau }}\int _{-\infty }^{t}exp(-(t-t')/\tau ){\dot {\gamma }}(t')dt'}$.

Le module de relaxation de la contrainte dans le cadre de ce modèle s'écrit :

${\displaystyle G^{*}=G'+iG''}$

avec

${\displaystyle G'={\frac {E\omega ^{2}\tau ^{2}}{1+\omega ^{2}\tau ^{2}}}}$

${\displaystyle G''={\frac {E\omega \tau }{1+\omega ^{2}\tau ^{2}}}}$

On peut remarquer que

${\displaystyle \left(G'-{\frac {E}{2}}\right)^{2}+G''^{2}={\frac {E^{2}}{4}}}$

est l'équation d'un cercle. Ainsi, la représentation de ${\displaystyle G''}$ en fonction de ${\displaystyle G'}$, dite représentation de Cole-Cole, est un demi cercle.

Remarque : la mise en parallèle d'un ressort et d'un amortisseur donne le modèle de Kelvin-Voigt.

Le modèle de Maxwell généralisé consiste à mettre en parallèle un nombre N fini d'éléments de Maxwell. Chacun de ces éléments répond aux relations énoncées ci-dessus. La contrainte totale est la somme des contraintes de chaque élément :

${\displaystyle \sigma (t)=\sum _{i=0}^{N}\sigma _{i}(t)=\sum _{i=0}^{N}{\frac {\eta _{i}}{\tau _{i}}}\int _{-\infty }^{t}exp(-(t-t')/\tau _{i}){\dot {\gamma }}(t')dt'}$.

Dans ce cas, le fluide ne comporte pas qu'un seul temps de relaxation, mais une collection ${\displaystyle \{\tau _{i}\}}$.

Cette équation peut se réécrire de la manière suivante :

${\displaystyle \sigma (t)=\int _{-\infty }^{t}G(t-t'){\dot {\gamma }}(t')dt'}$

où on a défini le module de relaxation des contraintes de cisaillement :

${\displaystyle G(t)=\sum _{i=0}^{N}{\frac {\eta _{i}}{\tau _{i}}}exp(-t/\tau _{i})}$.

• Relaxation de contrainte
• Modèle de Kelvin-Voigt
• Modèle de Maxwell convecté supérieur
• Liste de modèles rhéologiques