Relaxation de contrainte
La relaxation de contrainte est une des trois méthodes expérimentales d’analyse de la viscoélasticité linéaire, avec le fluage et les techniques dynamiques.
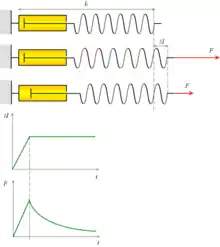
Dans un essai en quasi statique de relaxation, à partir d’un instant initial , une déformation (sollicitation) instantanée maintenue constante ou est appliquée à un échantillon, et la contrainte résultante (réponse), ou , est suivie en fonction du temps.
La relaxation est une propriété non instantanée : lorsqu’on impose un échelon de déformation, du fait du caractère viscoélastique du matériau, la contrainte met un certain temps à atteindre sa valeur finale. Le matériau retourne progressivement à un état plus stable. La relaxation, comme la viscoélasticité, fait intervenir les notions de résistance à l’écoulement, de viscosité, d’amortissement.
L’étude de ce mode de déformation courant, dépendant du temps, peut être réalisée en traction(-compression)[1] ou en cisaillement[2], au moyen d’un viscoanalyseur, à différentes températures.
On définit la fonction de relaxation en traction , qui est la variation de contrainte résultant de l’application d’une déformation constante, par la relation :
et pour un essai de cisaillement :
- .
La fonction module de relaxation (ou plus simplement le module de relaxation) en traction est le rapport de la contrainte à l’instant t à la déformation constante :
et la fonction module de relaxation en cisaillement s’écrit :
- .
Traitement d’une expérience de relaxation par le modèle de Maxwell
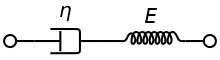
Si le comportement du matériau est simulé en utilisant le modèle de Maxwell (le modèle le plus simple du liquide viscoélastique), la vitesse de déformation est donnée par :
qui est l’équation régissant le modèle de Maxwell, avec :
- , la déformation longitudinale totale, égale à la somme de la déformation du ressort et de la déformation de l’amortisseur ;
- , une constante : le module de Young associé au ressort obéissant à la loi de Hooke[3] ;
- , la dérivée par rapport au temps de la contrainte ;
- , une constante : le coefficient de viscosité associé à l’amortisseur représentant le liquide newtonien.
La déformation est, par définition, maintenue constante () lors d’une expérience de relaxation, donc :
- .
La résolution de cette équation différentielle avec la condition initiale donne, après intégration, en posant (qui a la dimension d’un temps) :
- ,
montrant une décroissance exponentielle des contraintes avec le temps (elle se relaxe), avec un temps de relaxation ou temps de réponse[4], (noté aussi ), associé au modèle ; à un temps infini, il y a relaxation totale des contraintes.
Le module de relaxation se déduit de l’équation précédente :
- .
L’élasticité instantanée est égale à . Ce modèle prévoit un module tendant vers zéro si le temps tend vers l’infini, ce qui n’est pas réaliste.
Au cours d’un essai de relaxation, le modèle de Maxwell prévoit :
- si t << : comportement élastique ;
- si t ~ : comportement viscoélastique ;
- si t >> : comportement visqueux.
Cette comparaison entre t, le temps d'observation et le temps caractéristique du matériau donne le nombre de Deborah. Les modèles de Kelvin-Voigt et de Kelvin-Voigt généralisé ne permettent pas de décrire le comportement viscoélastique lors d’une expérience de relaxation.
La réponse viscoélastique d’un polymère est plus complexe que celle décrite par ces modèles rhéologiques car toutes les chaînes ne se réarrangent pas dans la même période de temps : la réponse du polymère est donnée en fonction d’une distribution des temps de réponse appelée spectre de (temps de) relaxation. Ce dernier dépend de la masse moléculaire, de la distribution des masses moléculaires et de la ramification. Plus la masse sera faible, plus la pente de la courbe du module de relaxation sera élevée.
Traitement d’une expérience de relaxation par le modèle de Maxwell généralisé
Si le matériau est décrit à l’aide du modèle de Maxwell généralisé aussi appelé modèle de Maxwell-Wiechert, le module de relaxation en traction est la somme des modules des différents éléments disposés en parallèle ; il s’exprime sous une forme simple :
avec :
- et , les paramètres viscoélastiques du modèle ;
- , le module à temps infini ;
- , les temps de relaxation associés aux différentes branches du modèle.
Ce développement de la fonction de relaxation en somme d’exponentielles est appelé série de Prony[5]. La contrainte diminue de façon exponentielle avec le temps. La réponse instantanée implique tous les éléments élastiques (ressorts) montés en parallèle. L’expression de la fonction ci-dessus s’applique aussi bien au comportement liquide (relaxation totale) qu’au comportement solide (relaxation partielle) ; dans ce dernier cas, une des branches du modèle de Maxwell généralisé se réduit à un simple ressort de coefficient de rigidité [6], qui représente l’élasticité du matériau à temps infini. Si est nul, le comportement aux temps longs est un écoulement visqueux.
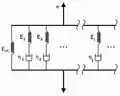 Modèle de Maxwell généralisé.
Modèle de Maxwell généralisé. Principe d’une expérience de relaxation, montrant la décroissance exponentielle des contraintes.
Principe d’une expérience de relaxation, montrant la décroissance exponentielle des contraintes.
Notes et références
- Par exemple, au milieu d’un essai de traction, on arrête de tirer sur l’éprouvette.
- Par exemple, au moyen d’un rhéomètre à déformation imposée (angle de rotation ϕ imposé), à plateaux parallèles.
- L’équation ci-dessus peut être appliquée au module de cisaillement G du ressort hookéen.
- À ne pas confondre avec le temps de retard utilisé dans une expérience de fluage.
- Voir aussi (en) Prony series.
- J. Bouton (Rhéo), G. Couarraze (Université Paris-Sud) et J.-L. Grossiord (Université Paris-Sud), Rhéologie et rhéométrie - Caractérisation de la viscosité, de la plasticité et de l’élasticité des liquides et des produits pâteux - Lois de comportement, fascicule, 50 p., éd. société Rhéo, Champlan.
































