Modèle de Kelvin-Voigt

Le modèle de Kelvin-Voigt est un modèle unidimensionnel décrivant le comportement mécanique d'un solide visqueux. En effet, lorsque l'on cesse d'appliquer un chargement à ce matériau, il retrouve (recouvre) toujours la même configuration (forme et dimensions). L'existence d'une configuration stable et unique sous chargement nul est caractéristique des solides, et les différencie des fluides.

Le modèle de Kelvin-Voigt est le modèle le plus simple rendant compte des phénomènes visqueux de fluage et de relaxation ; cependant, le fluage s'amorce ici pour tout chargement que l'on applique, aussi petit qu'il soit, ce qui n'est pas toujours le cas pour les solides visqueux réels : ce modèle ne comporte pas d'effet de seuil. Cela lui confère d'ailleurs un caractère de réversibilité : l'annulation des sollicitations provoque un retour complet du solide vers son état de référence, sans contraintes ni déformations résiduelles. Le solide de Kelvin-Voigt est, pour cette raison, un solide viscoélastique.

Représentation schématique du modèle de Kelvin–Voigt.

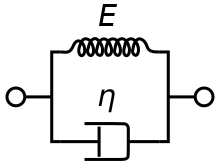
Le modèle de Kelvin-Voigt peut être représenté par un amortisseur purement visqueux et un ressort hookéen mis en parallèle comme l'indique le schéma ci-contre.

Dans le cas où les deux éléments sont placés en série, on obtient le modèle de Maxwell.

Dans ce modèle en parallèle, la déformation du ressort (R) est la même que celle de l'amortisseur (A) :

${\displaystyle \gamma _{\text{Total}}=\gamma _{A}=\gamma _{R}}$

Par ailleurs, la contrainte totale est la somme des contraintes du ressort et de l'amortisseur :

${\displaystyle \sigma _{\text{Total}}=\sigma _{R}+\sigma _{A}}$

Les contraintes de l'amortisseur et du ressort sont données respectivement par :

${\displaystyle \sigma _{A}=\eta {\dot {\gamma }}}$

${\displaystyle \sigma _{R}=E\gamma }$

où E est le module élastique associé au ressort et ${\displaystyle \eta }$ le coefficient de viscosité associé à l'amortisseur représentant un fluide newtonien.

On en déduit alors que :

${\displaystyle \sigma (t)=E\gamma (t)+\eta {\frac {d\gamma (t)}{dt}}}$

De même que pour le modèle de Maxwell, on en déduit un temps caractéristique de relaxation :

${\displaystyle \tau ={\frac {\eta }{E}}}$.

• Jean Mandel, Propriétés mécaniques des matériaux, Eyrolles, 1978, xi+284 (ASIN B0014LU108).
• Paul Germain, Mécanique des milieux continus, éd. Masson, 1962, 420 p. (ISBN 2-225-65197-3, ASIN B0014W1OGM), « Milieux viscoélastiques de Kelvin-Voigt ».

• Modèle de Maxwell
• Viscoanalyseur