Équation de Boltzmann
L' équation de Boltzmann ou équation de transport de Boltzmann décrit le comportement statistique d'un système thermodynamique hors état d' équilibre, conçue par Ludwig Boltzmann en 1872[1]. L'exemple classique d'un tel système est un fluide avec des gradients de température dans l'espace provoquant un flux de chaleur des régions les plus chaudes vers les plus froides, par le transport aléatoire mais orienté des particules composant ce fluide. Dans la littérature moderne, le terme équation de Boltzmann est souvent utilisé dans un sens plus général, se référant à toute équation cinétique décrivant le changement d'une quantité macroscopique dans un système thermodynamique, comme l'énergie, la charge ou le nombre de particules, que ce soit dans un cadre classique, semi-classique ou relativiste. Par exemple on a une équation de Boltzmann décrivant le transport de particules comme les photons (transfert radiatif) ou de pseudo-particules comme les phonons[2].
L'équation de Boltzmann est une des équations les plus importantes de la physique par l'étendue de ses applications (par exemple en mécanique des fluides) et par ses implications épistémologiques, en donnant un caractère universel au concept d'entropie introduit par Clausius en thermodynamique[3]. Elle jette un pont entre la physique microscopique (comportement individuel des composants d'un système) et la physique macroscopique (propriétés collectives comme l'énergie thermique, la viscosité, la conductivité électrique, etc.).
D'un point de vue mathématique, c'est une équation intégro-différentielle dont l'étude des propriétés et la recherche de solutions analytiques a fortement mobilisé les mathématiciens (Seiji Ukai dans les années 1970 ; ou plus récemment les médaillés Fields, Pierre-Louis Lions[4] et Cédric Villani[5]). Si l'existence de solutions est prouvée, même loin de l'équilibre, leur régularité et unicité reste un problème ouvert très important[6] - [7]. Mais dans la pratique, l'équation est résolue numériquement par différentes méthodes numériques (lagrangienne, eulérienne, particule-in-cell, etc.).
L'espace de phase et la fonction de densité
L'équation de Boltzmann détermine l'évolution d'un système de N particules (N très grand) dans l'espace des phases, espace qui contient l'ensemble des valeurs possibles des positions r et impulsions p des particules[8]. Chaque particule est représentée par 6 nombres . L'espace des phases complet est donc a priori un espace à 6 N dimensions, l'évolution au cours du temps du système étant déterminée par une trajectoire dans l'espace des phases , fonction (dite à N-corps) qui contient une quantité phénoménale d'information ; non calculable, elle n'a pas d'intérêt si on s'intéresse aux propriétés globales du système.
L'équation de Boltzmann est une équation à un corps qui considère la distribution de probabilité pour la position et l'impulsion d'une particule quelconque du système ; c'est-à-dire la probabilité qu'une particule occupe à un instant donné, une très petite région donnée de l'espace des phases, de volume autour de la position , et de volume ,autour de l'impulsion .
Le cœur de l'équation de Boltzmann est donc l'évolution au cours du temps de la fonction de densité de probabilité définie :
de sorte que est le nombre de toutes les molécules dont les positions et les impulsions sont situées dans l'élément de volume centré autour de . Cette fonction ne dépend plus de dans un système homogène dans l'espace ; dans un système homogène dans l'espace et isotrope en impulsion (la probabilité des vitesses est la même dans toutes les directions), le seul degré de liberté est l'énergie cinétique des particules , on obtient alors :
forme que l'on retrouve pour la distribution de probabilité des systèmes en équilibre thermique (voir infra).
L'intégration sur une région de l'espace des positions et de l'espace des impulsions donne le nombre total de particules qui ont des positions et des impulsions dans cette région (intégrale sextuple) :
La fonction à un corps f correspond au niveau le plus bas dans la hiérarchie BBGKY des équations du problème à N corps ; ce qui implique que l'on ne prend pas en compte les corrélations entre paires de particules, et donc
On suppose que les particules du système sont identiques (donc chacune a une masse m identique). Pour un mélange de plusieurs espèces chimiques, une distribution est nécessaire pour chacune d'entre elles, voir ci-dessous.
Principe de base
La fonction de distribution évolue au cours du temps en fonction de 3 facteurs : les forces exercées sur les particules par une influence externe (le modèle peut s'étendre aux forces s'exerçant entre les particules elles-mêmes dans l'hypothèse du champ moyen), la diffusion ("diff") des particules liée à leur mouvement dans l'espace, et leurs éventuelles collisions directes ("coll"). L'équation générale peut alors s'écrire
Les expressions détaillées de chacune de ces contributions sont fournies ci-dessous.
Note : certains auteurs utilisent la vitesse des particules v au lieu de la quantité de mouvement p ; grandeurs liées par la définition de la quantité de mouvement par .
Termes de force, de diffusion et de collision
Dans un système de particules décrit par la distribution , soumis à une force externe F, à un instant donné t, considérons le sous-ensemble de celles situées à la position r dans l'élément avec la quantité de mouvement p dans . Au temps , leur position sera et leur impulsion . En l'absence de collisions, la conservation du nombre de particules implique que la densité dans l'espace des phases est conservée, soit
Dans cette expression on utilise le fait que l'élément de volume de l'espace des phases est constant au cours du temps (conséquence du théorème de Liouville). La seule déviation de cette identité est causée par les collisions :
où est la variation totale de. En passant aux limites et , on obtient :
Par ailleurs, la conservation de la densité dans l'espace implique que, sans les collisions, la différentielle totale suivante soit nulle
avec le produit scalaire ( . ) et l'opérateur usuel gradient pour les positions, qui se formule de manière analogue pour les moments :
avec les vecteurs unitaires en coordonnées cartésiennes.
Forme finale
Regroupant tous les termes, on obtient l'équation de Boltzmann :
Dans ce contexte, est le champ de force agissant sur les particules du système, et m est la masse des particules. Lorsque les forces dérivent d'un potentiel , on peut exprimer l'équation de Boltzmann en fonction de l'hamiltonien avec le crochet de Poisson :
Lorsque les forces entre particules sont répulsives à longue portée, comme l'interaction coulombienne, les collisions directes sont impossibles ; on obtient l'équation de Boltzmann sans collision, généralement appelée équation de Vlassov. L'équation de Boltzmann quantique est obtenue lorsque la densité dans l'espace des phases et les collisions entre particules tiennent compte des effets du principe d'exclusion de Pauli pour les fermions.
Sans collisions, l'équation se réduit au formalisme classique de la mécanique hamiltonienne ; le calcul du terme de collision est donc essentiel et repose sur le type de statistique qui s'applique aux particules du système (Maxwell-Boltzmann, Fermi-Dirac ou Bose-Einstein).
Solutions à l'équilibre
Lorsque le système est homogène et n'est pas soumis à des forces externes, Boltzmann a démontré que la distribution f tend asymptotiquement vers une limite, qui est la distribution de probabilité de Maxwell-Boltzmann. Comme vu plus haut, le seul degré de liberté des particules étant leur énergie, la loi donne le nombre de particules dans un petit domaine d'énergie
où N est le nombre total de particules, T est la température d'équilibre, la constante de Boltzmann et la densité de niveaux d'énergie. Cette distribution correspond au maximum de l'entropie du système (voir Théorème H).
Dans le cas des photons (et autres particules traitées dans les problèmes de transfert radiatif) et des phonons c'est la statistique de Bose-Einstein qui doit être utilisée.
Le terme de collision (Stosszahlansatz) et le chaos moléculaire
Terme de collision à deux corps
Une idée clé de Boltzmann a été de calculer le terme de collision (ou « noyau de collision ») en le limitant aux collisions à deux corps entre des particules, supposées ponctuelles et non corrélées avant la collision. Cette hypothèse désignée comme le « Stosszahlansatz » et est également connue sous le nom d'« hypothèse du chaos moléculaire ». Sous cette hypothèse, et parce que l'interaction est locale dans l'espace des positions, le terme de collision peut être écrit comme une intégrale dans l'espace des impulsions sur le produit des fonctions de distribution à une particule[1], équation connue sous le nom d'équation de Wang Chang et Uhlenbeck[9] :

où et sont les impulsions de deux particules quelconques avant la collision (étiquetées A et B pour plus de commodité) ; et sont les impulsions après la collision ; la conservation des impulsions et de l'énergie (chocs élastiques) implique que , la valeur de la quantité de mouvement relative, soit conservée :
est la section efficace différentielle de la collision ; la collision se traduit donc par une rotation aléatoire d'un angle θ dans l'angle solide de la quantité de mouvement relative des particules (voir figure).
Ces quantités sont nommées « intégrales de collision » et sont calculables analytiquement dans le cas d'une interaction de type « sphère dure » ou peuvent être approximées numériquement par une loi simple dans le cas de potentiels intermoléculaires réalistes.
Le rôle du terme de collisions - un exemple
Pour illustrer le rôle du terme de collisions, on considère un système de particules, homogène dans l'espace : son évolution est donc limité à l'espace des moments. Pour simplifier la représentation, on se limite à deux dimensions.
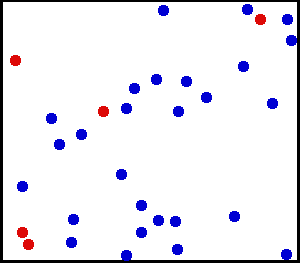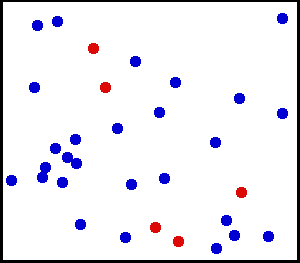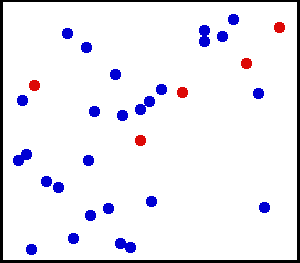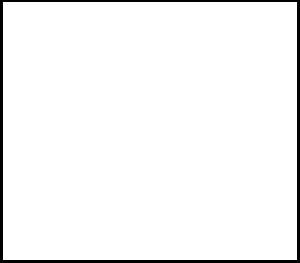
Dans son état initial, il est constitué de deux sous-systèmes de particules identiques, à l'équilibre thermique dans leur référentiel (température T=1 en unités arbitraires) ; les 2 sous-systèmes ont un mouvement relatif l'un par rapport à l'autre. La figure ci-contre donne l'évolution de la distribution dans l'espace des moments : résolution lagrangienne (voir ci-dessous la section « Résoudre l'équation ») avec un échantillon de 2 000 particules avant et après 10 000 collisions.
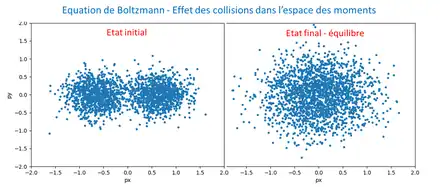
Initialement, le système est hors équilibre, avec un mouvement collectif le long de l'axe des x : son énergie se décompose en une énergie thermique propre aux 2 sous-systèmes et une énergie collective de translation (énergie libre, transformable en d'autres énergies, mécanique par exemple). Le système est d'entropie basse car partiellement ordonné.
Les collisions aléatoires entre les particules, supposées ponctuelles, conduisent à un état totalement thermalisé, d'entropie maximale (distribution symétrique en x et y, selon la formule de Maxwell). L'irréversibilité de l'évolution globale prend sa source dans le caractère aléatoire de la rotation du moment relatif (voir figure ci-dessus) lors des collisions binaires individuelles (chaos moléculaire).
Simplifications du terme de collision
Le principal défi dans la résolution de l'équation de Boltzmann provient du terme de collision. Désormais, la puissance des ordinateurs permet de faire les calculs explicites pour des milliers de particules en interaction, comme ci-dessus (voire beaucoup plus, voir simulation d'un système à N-corps).
Historiquement, des tentatives ont été faites pour «modéliser» et simplifier le terme de collision. L'équation modèle la plus connue est l'équation BGK due à Bhatnagar, Gross et Krook[10] ; elle est obtenue en faisant l'hypothèse que l'effet des collisions moléculaires est de forcer une fonction de distribution hors d'équilibre à revenir à la fonction d'équilibre (fonction maxwellienne dans le cas classique) en tous points de l'espace des positions, et que la vitesse à laquelle cela se produit est proportionnelle à la fréquence des collisions[11]. L'équation de Boltzmann est donc modifiée sous la forme BGK :
où est la fréquence de collision, et est la fonction de distribution locale (maxwellienne dans le cas classique, voir ci-dessus) compte tenu de la température du gaz en ce point de l'espace.
Cette approximation a été améliorée avec le modèle « ellipsoïdal »[12] plus proche de la physique car il préserve le bon nombre de Prandtl du milieu, et donc constitue une meilleure approximation des propriétés de transport.
Équation générale (pour un mélange)
Pour un mélange d'espèces chimiques étiquetées par les indices , l'équation pour une espèce i est [1]
où le terme de collision s'écrit :
avec les notations simplifiées et l'amplitude des moments relatifs est
et est la section efficace différentielle entre les particules des espèces i et j. La somme des intégrales décrit l'entrée et la sortie des particules d'espèces i dans ou hors de l'élément de l'espace des phases, sous l'effet des collisions avec les particules de toutes les espèces.
Applications et extensions
Équations de conservation
L'équation de Boltzmann peut être utilisée pour dériver les lois de conservation de la dynamique des fluides pour la masse, la charge, la quantité de mouvement et l'énergie[13]. Pour un fluide constitué d'un seul type de particules, la densité numérique (nombre de particules par unité de volume d'espace) est donnée par
La valeur moyenne locale de toute fonction est :
Étant donné que les équations de conservation impliquent des tenseurs, la convention de sommation d'Einstein sera utilisée : les indices répétés dans un produit indiquent une sommation sur ces indices. Ainsi et , où est le vecteur vitesse des particules.
Considérons une quantité , une fonction de la quantité de mouvement seulement, qui est conservée dans une collision. Supposons également que la force est une fonction de la position uniquement, et que la distribution est nulle pour . En multipliant l'équation de Boltzmann par A et en intégrant sur la quantité de mouvement, on obtient quatre termes qui, en utilisant l'intégration par parties, peuvent être exprimés comme :
où le dernier terme est nul, puisque A est conservé dans une collision élastique. Les valeurs de A correspondent aux moments de vitesse (et l'impulsion , car ils sont linéairement dépendants).
Moment zéro
Soit , la masse de la particule, l'équation de Boltzmann intégrée devient l'équation de conservation de la masse[13] :
où est la masse volumique, et est la vitesse moyenne du fluide.
Premier moment
Soit , la quantité de mouvement des particules, l'équation de Boltzmann intégrée devient l'équation de conservation de la quantité de mouvement [13] :
où est le tenseur de pression (soit le tenseur des contraintes visqueuses plus la pression hydrostatique, voir l'article Équations de Navier-Stokes pour leurs définitions).
Deuxième moment
Posant , l'énergie cinétique des particules, l'équation de Boltzmann intégrée devient l'équation de conservation de l'énergie[13] :
où est la densité d'énergie thermique cinétique, et est le vecteur de flux de chaleur.
Théorème de Lanford
En mécanique hamiltonienne, l'équation de Boltzmann s'écrit souvent plus généralement comme
où est l'opérateur de collision, opérateur intégral non linéaire.
Le théorème de Lanford étudie la validité de l'équation de Boltzmann lorsque les particules ne sont pas considérées comme ponctuelles.
Limite de Boltzmann-Grad
La limite dite de Boltzmann-Grad consiste à prendre la limite conjointe :
- d'un nombre de particules ;
- d'un rayon ;
en maintenant le produit . En particulier, le volume exclu tend vers zéro dans cette limite : .
Théorème de Lanford (1973)
Lanford a démontré rigoureusement[14] qu'un gaz de sphères dures dilué dans obéit à l'équation de Boltzmann dans la limite de Boltzmann-Grad, au moins pour un temps très court, égal seulement à un cinquième du temps de parcours moyen d'une particule.
En dépit de cette restriction sur la durée, ce théorème mathématique rigoureux est très important conceptuellement, puisque l'équation de Boltzmann entraîne le théorème H, à propos duquel Boltzmann fut accusé de pratiquer des « mathématiques douteuses ». Il n'en demeure pas moins qu'il reste à démontrer que ce résultat reste vrai pour des temps macroscopiques, ainsi que lorsque les atomes sont confinés dans une boîte.
Théorie quantique et violation de la conservation du nombre de particules
Il est possible d'écrire des équations de Boltzmann quantiques (ou plus exactement semi-classiques) qui prennent en compte les contraintes typiquement quantiques sur la densité dans l'espace des phases. L'équation la plus connue est obtenue en appliquant l'approximation du champ moyen pour les interactions moyenne entre particules et un terme de collisions modifié pour interdire les collisions conduisant à des états finaux interdits par le principe de Pauli : le terme de collision de Uehling-Uhlenbeck (en) (voir la référence[15] pour son étude en physique nucléaire).
De plus, dans aux hautes énergies, dans les systèmes quantiques relativistes le nombre de particules n'est pas conservé dans les collisions. Cela a plusieurs applications en cosmologie physique[16], y compris la formation des éléments légers dans la nucléosynthèse du Big Bang, la production de matière noire et la baryogénèse. Il n'est pas établi a priori que l'état d'un système quantique puisse être caractérisé par une densité d'espace de phase classique f. Cependant, pour une large classe d'applications, il existe une généralisation bien définie de f qui est la solution d'une équation de Boltzmann efficace qui peut être dérivée des premiers principes de la théorie quantique des champs[17].
L'absence de conservation du nombre de particules est également présente dans le cadre classique en neutronique[18].
Relativité générale et astronomie
L'équation de Boltzmann est utile en dynamique galactique. Une galaxie, sous certaines hypothèses, peut être représentée approximativement comme un fluide continu ; sa distribution de masse est alors représentée par la distribution f ; dans les galaxies, les collisions physiques entre les étoiles sont très rares, et l'effet des collisions gravitationnelles peut être négligé pendant des temps bien plus longs que l' âge de l'univers.
Dans un contexte relativiste, l'opérateur d'évolution relativiste s'écrit
où est le symbole de Christoffel de seconde espèce (cela suppose qu'il n'y a pas de forces externes, de sorte que les particules se déplacent le long des géodésiques en l'absence de collisions), avec la subtilité importante que la densité est une fonction dans l'espace des phases en mode mixte contravariant-covariant par opposition à l'espace des phases entièrement contravariant [19] - [20].
En cosmologie physique, l'approche entièrement covariante a été utilisée pour étudier le rayonnement de fond diffus cosmologique[21].Plus généralement, l'étude des processus dans l'univers primitif tente souvent de prendre en compte les effets de la mécanique quantique et de la relativité générale[16].Dans le milieu très dense formé par le plasma primordial après le Big Bang, des particules se créent et s'annihilent en permanence. Dans un tel environnement, la cohérence quantique et l'extension spatiale de la fonction d' onde peuvent affecter la dynamique, ce qui rend douteux que la distribution d'espace de phase classique f qui apparaît dans l'équation de Boltzmann soit appropriée pour décrire le système. Dans de nombreux cas, il est cependant possible de dériver une équation de Boltzmann efficace pour une fonction de distribution généralisée à partir des premiers principes de la théorie quantique des champs[17]. Cela inclut la formation des éléments légers dans la nucléosynthèse primordiale, la production de matière noire et la baryogénèse.
Résoudre l'équation
Des solutions exactes aux équations de Boltzmann se sont avérées exister dans certains cas[22] ; cette approche analytique donne un aperçu, mais n'est généralement pas utilisable dans des problèmes pratiques.
Au lieu de cela, les méthodes numériques sont généralement utilisées pour trouver des solutions approximatives aux différentes formes de l'équation de Boltzmann.
Les méthodes de résolution numérique directe
Il existe de très nombreuses méthodes de résolution numérique de l'équation de Boltzmann, adaptées au contexte physique (voir sous-section "Exemples d'applications" ci-dessous). On peut schématiquement les classer en deux grandes familles.
Les méthodes eulériennes
L'espace des phases (dans le cas le plus général à 6 dimensions) est discrétisé en un réseau de mailles, soit régulières, soit de taille adaptable. La fonction de distribution est est calculée aux sommets des mailles, l'évolution au cours du temps liée au terme dispersif et aux forces externes ou internes de l'hamiltonien est calculée par les éléments finis ; les intégrales du terme de collision sont plus complexes à évaluer et souvent l'approximation simplificatrice BGK est utilisée (voir ci-dessus). Les calculs sur réseaux nécessitent des tailles de mémoire importantes, si l'on veut une discrétisation suffisante dans chacun des axes de l'espace des phases : par exemple 10 pas de calcul par axe -ce qui est peu- conduisent à un réseau de sommets.
Les méthodes lagrangiennes
Elles sont basées sur des méthodes de Monte Carlo : on suit au cours du temps un échantillon de N particules, dont les coordonnées sont générées aléatoirement, selon la fonction de distribution initiale :
L' évolution au cours du temps de la distribution se déduit du calcul des trajectoires des N particules : a) par les équations d'Hamilton pour prendre en compte les forces externes ou le champ moyen interne, b) par le calcul explicite des collisions binaires, lorsque les trajectoires se croisent à une distance inférieure à la distance d'approche liée à la section efficace.
Les caractéristiques (masse, charge, section efficace, etc.) des particules de l'échantillon doivent être renormalisées par rapport aux caractéristiques des particules physiques pour conserver les propriétés globales du système. Les grandeurs moyennes du système sont calculables à chaque instant par sommation sur les particules de l'échantillon.
Comme toute méthode de Monte Carlo, la précision des résultats dépend du ratio ; les méthodes lagrangiennes sont très flexibles et très adaptées à l'étude des systèmes dynamiques dont l'extension dans l'espace des phases varie beaucoup ou cours du temps.
Exemples d'applications
Les exemples d'applications vont de l'aérodynamique hypersonique dans les flux de gaz raréfiés [23] - [24], aux flux de plasma[25] et à la physique du solide avec l'équation de Boltzmann-Peierls. Une application de l'équation de Boltzmann en électrodynamique est le calcul de la conductivité électrique - le résultat est au premier ordre identique au résultat semi-classique[26]. Une formulation semi-classique est très utilisée en physique nucléaire pour l'étude des réactions avec des noyaux lourds[15].
Résolution des systèmes dérivés
Lorsque le système est proche de l'équilibre local, la solution de l'équation de Boltzmann peut être représentée par celle des moments de la fonction de distribution décrits plus haut et des quantités associées.
L'exemple classique est le développement asymptotique en puissances du nombre de Knudsen (le développement de Chapman-Enskog [27]). Les deux premiers termes de ce développement donnent les équations d'Euler et les équations de Navier-Stokes. Les termes supérieurs introduits par David S. Burnett ont des singularités.
Une autre méthode est basée sur la fermeture du système aux moments par une hypothèse ad hoc. Un premier exemple est la méthode de Grad qui suppose la solution décrite par une série de polynômes d'Hermite. Une solution plus élégante consiste à minimiser l'entropie du système[28]. Cette méthode, d'abord appliquée aux milieux gazeux sans montrer d'avantage par rapport à la méthode classique, a montré son efficacité dans le domaine du transfert radiatif (méthode MN).
Le problème du développement mathématique des processus limites, qui conduisent de la vision atomistique (représentée par l'équation de Boltzmann) aux lois du mouvement des continus, est une partie importante du sixième problème de Hilbert[29].
Limitations et autres utilisations de l'équation de Boltzmann
L'équation de Boltzmann n'est valable que sous plusieurs hypothèses. Par exemple, les particules sont supposées être ponctuelles, c'est-à-dire sans avoir une taille finie. Il existe une généralisation de l'équation de Boltzmann qui s'appelle l'équation d'Enskog[30] (voir plus haut).
Les particules sont supposées n'avoir aucun de degré de liberté interne, aussi les collisions sont considérées comme élastiques. S'il existe un degré de liberté interne, l'équation de Boltzmann doit être généralisée pour prendre en compte des collisions inélastiques[9] - [30].
De nombreux fluides réels comme les liquides ou les gaz denses ont en plus des caractéristiques mentionnées ci-dessus des formes de collisions plus complexes, il y aura non seulement des collisions binaires, mais aussi ternaires et d'ordre supérieur. Celles-ci doivent être dérivées en utilisant la hiérarchie BBGKY.
Une équation de type Boltzmann est utilisée en transfert radiatif pour les problèmes de rayonnement pour photons, neutrinos, neutrons, particules , ions, phonons…
Ce type d'équation est également utilisé pour le mouvement des cellules[31] - [32]. Puisque les cellules sont des particules composites qui portent un degré de liberté interne, les équations de Boltzmann généralisées correspondantes doivent avoir des intégrales de collision inélastiques. De telles équations peuvent décrire les invasions de cellules cancéreuses dans les tissus, la morphogenèse et les effets liés à la chimiotaxie .
Références
- (en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Boltzmann equation » (voir la liste des auteurs).
- (en) Rita G. Lerner et G. L. Trigg, Encyclopaedia of Physics (2nd Edition), VHC publishers, (ISBN 0-89573-752-3)
- (en) Joseph Callaway, Quantum Theory of the Solid State, Academic Press,
- Eduardo Arroyo Pérez, L'univers va-t-il vers la mort thermique ? : Boltzmann et l'entropie, RBA France, impr. 2015, cpop. 2015 (ISBN 978-2-8237-0235-4 et 2-8237-0235-0, OCLC 921143034, lire en ligne)
- R-J. Di Perna et P-L. Lions, « Solutions globales de l’équation de Boltzmann », Séminaire Équations aux dérivées partielles (Polytechnique) (1987-1988) [PDF]
- Cédric Villani, « Contribution à l'étude mathématique des équations de Boltzmann et de Landau en théorie cinétique des gaz et des plasmas », Thèse de doctorat [PDF], (consulté le )
- DiPerna et Lions, « On the Cauchy problem for Boltzmann equations: global existence and weak stability », Ann. of Math., 2e série, vol. 130, no 2, , p. 321–366 (DOI 10.2307/1971423, JSTOR 1971423)
- Philip T. Gressman et Robert M. Strain, « Global classical solutions of the Boltzmann equation with long-range interactions », Proceedings of the National Academy of Sciences, vol. 107, no 13, , p. 5744–5749 (PMID 20231489, PMCID 2851887, DOI 10.1073/pnas.1001185107, Bibcode 2010PNAS..107.5744G, arXiv 1002.3639)
- Hélène Ngô et Christian Ngô, Physique statistique : introduction, avec exercices, Masson, (ISBN 2-225-81287-X et 978-2-225-81287-3, OCLC 19904032, lire en ligne)
- Raymond Brun, Introduction à la dynamique des gaz réactifs, Toulouse, Cépaduès, , 402 p. (ISBN 978-2-36493-190-9)
- Bhatnagar, Gross et Krook, « A Model for Collision Processes in Gases. I. Small Amplitude Processes in Charged and Neutral One-Component Systems », Physical Review, vol. 94, no 3, , p. 511–525 (DOI 10.1103/PhysRev.94.511, Bibcode 1954PhRv...94..511B)
- Lev Landau et Evgeneij Lifchitz, Physique statistique, Éd. Mir, (ISBN 2-7298-9463-2 et 978-2-7298-9463-4, OCLC 464219360, lire en ligne)
- (en) Stéphane Brull et Seok-Bae Yun, « Stationary Flows of the ES-BGK Model with the Correct Prandl Number »
- S. R. de Groot et P. Mazur, Non-Equilibrium Thermodynamics, New York, Dover Publications Inc., (ISBN 978-0-486-64741-8)
- Oscar E. Lanford III, Time Evolution of Large Classical Systems, dans : Dynamical Systems, Theory and Application, J. Moser (éd.), Springer-Verlag (1975). Lire également : Oscar E. Lanford III, On a derivation of the Boltzmann equation, dans : Nonequilibrium phenomena I: The Boltzmann equation, Joël L. Lebowitz & Elliott W. Montroll (éd.), North-Holland (1983), 3-17.
- Christian Grégoire, « Effets des collisions sur la dynamique nucléaire » [PDF], (consulté le )
- Edward Kolb et Michael Turner, The Early Universe, Westview Press, (ISBN 9780201626742)
- M. Drewes, C. Weniger et S. Mendizabal, « The Boltzmann equation from quantum field theory », Phys. Lett. B, vol. 718, no 3, , p. 1119–1124 (DOI 10.1016/j.physletb.2012.11.046, Bibcode 2013PhLB..718.1119D, arXiv 1202.1301, S2CID 119253828)
- Anne-Marie Baudron, Patrick Blanc-Tranchant, Mireille Coste-Delclaux, Cheikh M. Diop, Jean-Jacques Lautard et Anne Nicol, « Les méthodes de la neutronique », sur CEA
- Debbasch et Willem van Leeuwen, « General relativistic Boltzmann equation I: Covariant treatment », Physica A, vol. 388, no 7, , p. 1079–1104 (DOI 10.1016/j.physa.2008.12.023, Bibcode 2009PhyA..388.1079D)
- Debbasch et Willem van Leeuwen, « General relativistic Boltzmann equation II: Manifestly covariant treatment », Physica A, vol. 388, no 9, , p. 1818–34 (DOI 10.1016/j.physa.2009.01.009, Bibcode 2009PhyA..388.1818D)
- Maartens R, Gebbie T, Ellis GFR (1999). "Cosmic microwave background anisotropies: Nonlinear dynamics". Phys. Rev. D. 59 (8): 083506
- Philip T. Gressman, Robert M. Strain, « Global Classical Solutions of the Boltzmann Equation without Angular Cut-off », Journal of the American Mathematical Society, vol. 24, no 3, , p. 771 (DOI 10.1090/S0894-0347-2011-00697-8, arXiv 1011.5441, S2CID 115167686)
- Evans, Morgan et Hassan, « A discontinuous finite element solution of the Boltzmann kinetic equation in collisionless and BGK forms for macroscopic gas flows », Applied Mathematical Modelling, vol. 35, no 3, , p. 996–1015 (DOI 10.1016/j.apm.2010.07.027, lire en ligne)
- Evans et Walton, « Aerodynamic optimisation of a hypersonic reentry vehicle based on solution of the Boltzmann–BGK equation and evolutionary optimisation », Applied Mathematical Modelling, vol. 52, , p. 215–240 (ISSN 0307-904X, DOI 10.1016/j.apm.2017.07.024, lire en ligne)
- Pareschi et Russo, « Numerical Solution of the Boltzmann Equation I: Spectrally Accurate Approximation of the Collision Operator », SIAM Journal on Numerical Analysis, vol. 37, no 4, , p. 1217–1245 (ISSN 0036-1429, DOI 10.1137/S0036142998343300, CiteSeerx 10.1.1.46.2853)
- H.J.W. Müller-Kirsten, Basics of Statistical Mechanics, Chapter 13, 2nd ed., World Scientific (2013), (ISBN 978-981-4449-53-3).
- (en) Sydney Chapman et Thomas George Cowling, The mathematical theory of non-uniform gases: an account of the kinetic theory of viscosity, thermal conduction, and diffusion in gases, Cambridge University Press, (ISBN 0-521-40844-X, lire en ligne)
- (en) Charles David Levermore, « Moment Closure Hierarchies for Kinetic Theories », Journal of Statistical Physics, vol. 83, (lire en ligne)
- « Theme issue 'Hilbert's sixth problem' », Philosophical Transactions of the Royal Society A, vol. 376, no 2118, (DOI 10.1098/rsta/376/2118)
- « Enskog Equation - an overview | ScienceDirect Topics », www.sciencedirect.com (consulté le )
- Chauviere, A.; Hillen, T.; Preziosi, L., « Modeling cell movement in anisotropic and heterogeneous network tissues », American Institute of Mathematical Sciences, vol. 2, no 2, , p. 333–357 (DOI 10.3934/nhm.2007.2.333, lire en ligne)
- (en) Conte et Loy, « Multi-Cue Kinetic Model with Non-Local Sensing for Cell Migration on a Fiber Network with Chemotaxis », Bulletin of Mathematical Biology, vol. 84, no 3, , p. 42 (ISSN 1522-9602, PMID 35150333, PMCID 8840942, DOI 10.1007/s11538-021-00978-1, lire en ligne)
Bibliographie
- Anouk Barberousse, La mécanique statistique - De Clausius à Gibbs, Collection Histoire des Sciences, Belin (2002) (ISBN 2-7011-3073-5). Cette collection originale propose une histoire du développement de la théorie cinétique des gaz basée sur des extraits des grands textes fondateurs (traduits en français) mis en perspective contemporaine par une historienne des sciences (CNRS). Accessible dès le niveau premier cycle universitaire.
- Ludwig Boltzmann, Leçons sur la théorie des gaz, Gauthier-Villars (1902-1905). Réédition Jacques Gabay (1987) (ISBN 2-87647-004-7).
- Carlo Cercignani, Ludwig Boltzmann - The man who Trusted Atoms, Oxford University Press (1998) 330 p. (ISBN 0-19-850154-4). Biographie scientifique du professeur Boltzmann, qui a porté la théorie cinétique des gaz à son acmée. Par un professeur de Physique mathématique de l'université de Milan (Italie), spécialiste de l'équation de Boltzmann. Niveau plutôt second cycle universitaire.
- Carlo Cercignani, The Boltzmann Equation & its Applications, Series: Applied Mathematical Sciences, 67, Springer-Verlag (1987) (ISBN 0-387-96637-4).
- Carlo Cercignani, Reinhard Illner et Mario Pulvirenti, The Mathematical Theory of Dilute Gases, Series: Applied Mathematical Sciences, 106, Springer-Verlag (1994) (ISBN 0-387-94294-7).
- Carlo Cercignani et Gilberto M. Kremer, The Relativistic Boltzmann Equation: Theory and Applications, Series: Progress in Mathematical Physics, 22, Birkhäuser (2002) (ISBN 3-7643-6693-1).
- Lawrence Sklar, Physics and Chance - Philosophical Issues in the Foundations of Statistical Mechanics, Cambridge University Press (1995) (ISBN 0-521-55881-6).
- Stewart Harris, An introduction to the theory of the Boltzmann equation, Dover Books, , 221 p. (ISBN 978-0-486-43831-3, lire en ligne). Introduction très peu coûteuse au cadre moderne (à partir d'une déduction formelle de Liouville et de la hiérarchie Bogoliubov–Born–Green–Kirkwood–Yvon (BBGKY) dans laquelle se place l'équation de Boltzmann). La plupart des manuels de mécanique statistique comme Huang traitent encore le sujet en utilisant les arguments originaux de Boltzmann. Pour dériver l'équation, ces livres utilisent une explication heuristique qui ne fait pas ressortir la plage de validité et les hypothèses caractéristiques qui distinguent les équations de Boltzmann des autres équations de transport comme les équations de Fokker-Planck ou de Landau.
- Arkeryd, « On the Boltzmann equation part I: Existence », Arch. Rational Mech. Anal., vol. 45, no 1, , p. 1–16 (DOI 10.1007/BF00253392, Bibcode 1972ArRMA..45....1A, S2CID 117877311)
- Arkeryd, « On the Boltzmann equation part II: The full initial value problem », Arch. Rational Mech. Anal., vol. 45, no 1, , p. 17–34 (DOI 10.1007/BF00253393, Bibcode 1972ArRMA..45...17A, S2CID 119481100)
- DiPerna et Lions, « On the Cauchy problem for Boltzmann equations: global existence and weak stability », Ann. of
Math., 2e série, vol. 130, no 2, , p. 321–366 (DOI 10.2307/1971423, JSTOR 1971423)














![{\displaystyle {\begin{aligned}N&=\int \limits _{\mathrm {moments} }{\text{d}}^{3}\mathbf {p} \int \limits _{\mathrm {positions} }{\text{d}}^{3}\mathbf {r} \,f(\mathbf {r} ,\mathbf {p} ,t)\\[5pt]&=\iiint \limits _{\mathrm {moments} }\quad \iiint \limits _{\mathrm {positions} }f(x,y,z,p_{x},p_{y},p_{z},t)\,{\text{d}}x\,{\text{d}}y\,{\text{d}}z\,{\text{d}}p_{x}\,{\text{d}}p_{y}\,{\text{d}}p_{z}\end{aligned}}}](https://img.franco.wiki/i/866caff05f0a12486dc4a29dc0bcb9401ddc3576.svg)










![{\displaystyle {\displaystyle {\begin{aligned}dN_{\mathrm {coll} }&=\left({\frac {\partial f}{\partial t}}\right)_{\mathrm {coll} }\,\Delta t\;d^{3}\mathbf {r} \,d^{3}\mathbf {p} \\[5pt]&=f\left(\mathbf {r} +{\frac {\mathbf {p} }{m}}\Delta t,\mathbf {p} +\mathbf {F} \Delta t,t+\Delta t\right)d^{3}\mathbf {r} d^{3}\mathbf {p} -f(\mathbf {r} ,\mathbf {p} ,t)\,d^{3}\mathbf {r} \,d^{3}\mathbf {p} \\[5pt]&=\Delta f\,d^{3}\mathbf {r} \,d^{3}\mathbf {p} \;;\end{aligned}}}}](https://img.franco.wiki/i/5e8462bd60a8320d1dd66c7da1ac34cf7c1e52e7.svg)





![{\displaystyle {\displaystyle {\begin{aligned}df&={\frac {\partial f}{\partial t}}\,dt+\left({\frac {\partial f}{\partial x}}\,dx+{\frac {\partial f}{\partial y}}\,dy+{\frac {\partial f}{\partial z}}\,dz\right)+\left({\frac {\partial f}{\partial p_{x}}}\,dp_{x}+{\frac {\partial f}{\partial p_{y}}}\,dp_{y}+{\frac {\partial f}{\partial p_{z}}}\,dp_{z}\right)\\[5pt]&={\frac {\partial f}{\partial t}}dt+\nabla _{\mathbf {r} }f\cdot d\mathbf {r} +{\nabla _{p}f}\cdot d\mathbf {p} \\[5pt]&={\frac {\partial f}{\partial t}}dt+\nabla _{\mathbf {r} }f\cdot {\frac {\mathbf {p} }{m}}dt+{\nabla _{p}f}\cdot \mathbf {F} \,dt\end{aligned}}}}](https://img.franco.wiki/i/1111addef73cf569ad441e8487557096984530c8.svg)












![{\displaystyle \left({\frac {\partial f}{\partial t}}\right)_{\text{coll}}=\iint g\,I(g,\Omega )[f(\mathbf {r} ,\mathbf {p} '_{A},t)f(\mathbf {r} ,\mathbf {p} '_{B},t)-f(\mathbf {r} ,\mathbf {p} _{A},t)f(\mathbf {r} ,\mathbf {p} _{B},t)]\,d\Omega \,d^{3}\mathbf {p} _{B}}](https://img.franco.wiki/i/d82abcf2eec2e94f180c5953bdea9cc8ddfbae4c.svg)














![{\displaystyle \left({\frac {\partial f_{i}}{\partial t}}\right)_{\mathrm {coll} }=\sum _{j=1}^{n}\iint g_{ij}I_{ij}(g_{ij},\Omega )[f'_{i}f'_{j}-f_{i}f_{j}]\,d\Omega \,d^{3}\mathbf {p'} }](https://img.franco.wiki/i/253a2b55d6c4b75ffa65c96c3c09300e5b5c1a85.svg)






























![{\hat {{\mathbf {L}}}}[f]\ =\ {\mathbf {C}}[f]](https://img.franco.wiki/i/2eca8da533760d87f771e6440af7476cb6d1ebae.svg)
















