Méthode MN

En prémultipliant l'équation de Boltzmann par 1, μ, ... et en intégrant sur μ on obtient un système sur les moments de la luminance

${\displaystyle {\begin{array}{lcl}{\frac {\partial E}{\partial t}}+\mu {\frac {\partial M}{\partial x}}&=&\kappa _{a}(4\pi B-cE)\\[0.6em]{\frac {\partial M}{\partial t}}+c^{2}\mu {\frac {\partial P}{\partial x}}&=&-c\kappa _{f}(x,t)M\\[0.6em]...\end{array}}}$

où apparaît le premier moment de la fonction de phase g₁

${\displaystyle \kappa _{f}(x,t)=\kappa _{a}(x,t)+[1-g_{1}\kappa _{d}(x,t)]\,,\qquad g_{1}=\int _{-1}^{1}P(\alpha )\alpha \mathrm {d} \alpha }$

g₁ = 0 pour toute distribution symétrique : distribution isotrope ou diffusion Thomson par exemple.

Le système sur les valeurs intégrées en fréquence est le même (en remplaçant 4 π B par a T⁴) puisqu'on a supposé les coefficients indépendants de celle-ci.

Par substitution dans le système ci-dessus on voit que celui-ci est entièrement décrit par E, f et χ, ces deux dernières valeurs jouant le rôle de nombres adimensionnels. Ils sont appelés premier et second facteur d'Eddington dans la théorie à N moments.

Ces moments sont des moments de Hausdorff et possèdent un certain nombre de propriétés[4]

• les symétries du problème entraînent    ${\displaystyle {\frac {1}{3}}\leq \chi \leq 1}$

χ = 1 / 3 correspond à l'isotropie et χ = 1 à un rayon.

• l'inégalité de Cauchy-Schwarz impose  ${\displaystyle \chi \geq f^{2}}$

Par ailleurs :

• ${\displaystyle |f|\leq 1}$ : cette inégalité découle des expressions précédentes. Elle exprime que le flux maximal possible correspond au transfert de l'énergie à la vitesse c

${\displaystyle |M_{max}|=cE}$

• le système décrit ci-dessus est hyperbolique. En supposant que les valeurs propres du système croissent avec | f | on montre que χ est une fonction convexe de f et que la dérivée χ' (f) vérifie | χ' (±1) | = 2 afin que la vitesse caractéristique en χ = ±1 (correspondante à un rayon lumineux) soit ±c.

On voit que f et χ sont sévèrement limités. Ceci a incité les physiciens à proposer un certain nombre de fermetures du type χ = g (f) appelées méthodes à facteur d'Eddington variable.

Distribution angulaire pour diverses valeurs de f (0, 0.3, 0.7, 0.9) dans la méthode M₁ (la direction du flux est ici π / 4 ).

Le système ci-dessus est, comme tout système aux moments, incomplet : chaque équation sur un moment fait apparaître un moment d'ordre supérieur inconnu. Au-delà du travail initial de Gerald Minerbo une méthode générale a été introduite par David Levermore[5]. Elle utilise l'entropie volumique spectrale d'un gaz de photons[6]

${\displaystyle {\mathcal {S}}(L)=[(n+1)\ln(n+1)-n\ln n]\,{\frac {2k\nu ^{2}}{c^{3}}}\,,\qquad n={\frac {c^{2}}{2h\nu ^{3}}}\,L}$

où n est le nombre d'occupation.

La fermeture consiste à choisir la luminance spectrale qui maximise l'entropie sous la contrainte de respecter les moments pris en compte. Ceci est toujours possible, l'entropie étant une fonction convexe de L. Un exemple est celui de la recherche de la fonction d'équilibre thermodynamique B supposée inconnue

${\displaystyle {\mathcal {S}}(B)=\min _{L}\{{\mathcal {S}}(L):{\frac {1}{c}}\langle L\rangle =aT^{4}\}}$

La solution de cette équation est la distribution de Planck définie plus haut.

Dans le cas général on note m = (1, μ, μ²,...). Le problème de minimisation s'écrit

${\displaystyle {\mathcal {S}}(B)=\min _{L}\{{\mathcal {S}}(L):\langle \mathbf {m} L\rangle ={\mathcal {M}}_{i}\}}$

où ℳ₀, ℳ₁, ℳ₂,...(ces quantités sont l'énergie, le flux, la pression,... et sont ici des paramètres du problème) sont les moments à respecter. On leur substitue les moments adimensionnés f, χ,.... La solution de ce problème est la fonction duale au sens de Legendre de l'entropie

${\displaystyle B={\frac {2h\nu ^{3}}{c^{2}}}{\frac {1}{e^{{\frac {hc\nu }{k}}(\alpha _{0}+\alpha _{1}\mu +\alpha _{2}\mu ^{2}+...)}-1}}}$

La démonstration est identique à celle de l'encadré précédent. La solution obtenue correspond à un spectre de corps noir et à une distribution angulaire d'autant plus complexe que l'ordre est élevé.

Dans le cas où l'on prend les deux premiers moments la solution appelée M₁ est analytique[7] et conduit à la relation de fermeture

${\displaystyle \chi ={\frac {3+4f^{2}}{5+2{\sqrt {4-3f^{2}}}}}}$

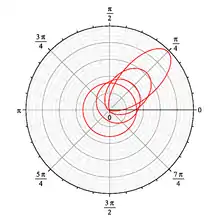
Il n'est pas nécessaire de connaître la distribution angulaire qui est sous-jacente dans le problème résolu. Celle-ci est régulière (voir courbe jointe) pouvant aller de l'isotropie au rayon. La méthode M₂ permet d'obtenir des distributions plus complexes[8].

Le caractère hyperbolique[7] permet d'utiliser des solveurs numériques efficaces développés pour la mécanique des fluides. Le couplage avec l'hydrodynamique en est grandement facilité[9] - [10]. La solution du système couplé est entropique (l'entropie du système croît au cours du temps) ce qui assure un bon comportement numérique.

Une pathologie de cette méthode est la possibilité de discontinuités de la solution comme en mécanique des fluides : des « chocs radiatifs » sans existence physique rencontrés lors du croisement de deux faisceaux. Ce problème n'existe que pour les développements de moments à l'ordre impair[11]. Ils peuvent être surmontés par une méthode de partition de l'espace analogue à la méthode à deux flux[12], laquelle n'est guère utilisée, le problème ne se posant généralement pas.

La méthode a été étendue au problème multidimensionnel en espace où M est une quantité vectorielle et P et les moments suivants des quantités tensorielles[7] et à un spectre quelconque en utilisant le découpage en bandes de fréquences[13]. Il existe également des travaux sur la méthode M₂ utilisant l'entropie de Maxwell-Boltzmann[14].

Distributions angulaires dans une lame isotherme en x / e = 0.95 et κ e = 3 (rouge : solution exacte, vert : méthode M₁).

Prenons l'exemple très simple du rayonnement dans et hors d'une lame d'épaisseur e, de température T, émissive et absorbante mais non diffusante, en régime stationnaire. Le repère utilisé a son origine sur l'une des faces et pointe vers l'intérieur du domaine. L'équation de Boltzmann est ici

${\displaystyle \mu {\frac {\mathrm {d} L^{R}}{\mathrm {d} x}}=\kappa _{a}(aT^{4}-L^{R})}$

La solution de ce problème différentiel linéaire du premier ordre est

${\displaystyle 4\pi L^{R}=\left\{{\begin{array}{lc}acT^{4}\left(1-e^{-{\frac {\kappa x}{\mu }}}\right)&\mu \geq 0\\[0.5em]acT^{4}\left[1-e^{-{\frac {\kappa (e-x)}{\mu }}}\right]&\mu <0\end{array}}\right.}$

${\displaystyle M^{R}=2\sigma T^{4}\left\{E_{3}[\kappa _{a}(x-e)]-E_{3}(\kappa _{a}x)\right\}}$

${\displaystyle E^{R}={\frac {aT^{4}}{2}}\left\{2-E_{2}[\kappa _{a}(x-e)]-E_{2}(\kappa _{a}x)\right\}}$

où E_i est l'exponentielle intégrale d'ordre i.

Cet exemple a le mérite d'être simple et donc de permettre de tester le cas plus général d'un spectre quelconque en permettant un calcul de référence raie par raie[13]. La comparaison avec la solution M₁ (voir courbe ci-contre) montre que la distribution angulaire n'est que médiocrement approchée, ce qui ne fait pas de la méthode une bonne candidate pour les problèmes d'optique. Pourtant l'erreur sur le flux sortant n'excède pas 3%. Ce chiffre se compare à la méthode SN ou à la méthode PN avec N ≈ 10, pour un coût calcul notablement moindre. Une telle erreur doit être rapprochée de la connaissance sur les coefficients d'absorption qui sont de l'ordre de 10% dans les meilleurs cas[15].

• Méthode PN