Angle solide

L'angle solide élémentaire (ou élément d'angle solide) ${\displaystyle \mathrm {d} ^{2}\Omega }$ correspondant à une surface infinitésimale d'aire ${\displaystyle \mathrm {d} ^{2}\!S}$ s'exprime sous la forme[1] :

${\displaystyle \mathrm {d} ^{2}\Omega ={\frac {{\vec {u}}\cdot {\overrightarrow {\mathrm {d} ^{2}\!S}}}{r^{2}}}={\frac {{\vec {r}}\cdot {\overrightarrow {n}}}{r^{3}}}\,\mathrm {d} ^{2}\!S}$,

où :

• ${\displaystyle {\vec {u}}}$ est le vecteur unitaire dirigé du sommet de l'angle solide élémentaire vers l'élément de surface ;
• ${\displaystyle {\overrightarrow {\mathrm {d} ^{2}\!S}}}$ est le vecteur normal à la surface et de norme ${\displaystyle \mathrm {d} ^{2}\!S}$ ;
• ${\displaystyle r}$ est la distance qui sépare le sommet de l'angle solide élémentaire de l'élément de surface ;
• ${\displaystyle {\vec {r}}=r\,{\vec {u}}}$ est le vecteur reliant le sommet de l'angle solide élémentaire à l'élément de surface ;
• ${\displaystyle {\vec {n}}}$ est le vecteur unitaire donnant la direction de l'élément de surface (${\displaystyle {\overrightarrow {\mathrm {d} ^{2}\!S}}=\mathrm {d} ^{2}\!S\ {\vec {n}}}$) ;

L'angle solide sous lequel on voit une surface ${\displaystyle S}$ à partir d'un point ${\displaystyle O}$ est donné par l'intégrale de surface :

${\displaystyle \Omega =\int \!\!\!\!\!\int _{S}{\frac {\overrightarrow {u}}{r^{2}}}\cdot {\overrightarrow {\mathrm {d} ^{2}S}}=\int \!\!\!\!\!\int _{S}{\frac {{\overrightarrow {r}}\cdot {\overrightarrow {n}}}{r^{3}}}\ {\mathrm {d} ^{2}S}}$.

Autrement dit, l'angle solide est égal au flux du champ ${\displaystyle {\overrightarrow {r}}/r^{3}}$ à travers la surface considérée[1].

Notations utilisées.

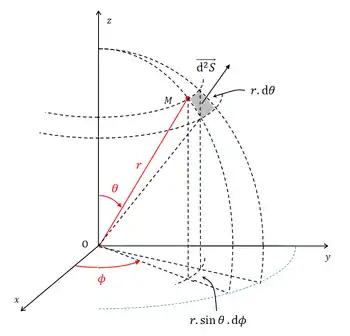
Pour une sphère de rayon ${\displaystyle r}$, l'angle solide élémentaire ${\displaystyle \mathrm {d} ^{2}\Omega }$ est défini pour un élément de surface élémentaire ${\displaystyle \mathrm {d} ^{2}S}$, correspondant à des variations angulaires infinitésimales des altitude ${\displaystyle \theta }$ et azimut ${\displaystyle \phi }$ (dans le cadre du calcul différentiel, la surface élémentaire est assimilée à un plan) :

${\displaystyle \mathrm {d^{2}S} =r\ \mathrm {d} \theta \ r\sin \theta \ \mathrm {d} \phi =r^{2}\ \sin \theta \ \mathrm {d} \phi \ \mathrm {d} \theta }$,

d'où :

${\displaystyle \mathrm {d} ^{2}\Omega =\sin \theta \ \mathrm {d} \phi \ \mathrm {d} \theta }$.

L'angle solide ${\displaystyle \Omega }$ correspond à un cône de révolution d'angle au sommet ${\displaystyle 2\alpha }$ inscrit dans la sphère de projection

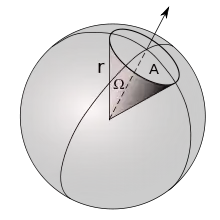
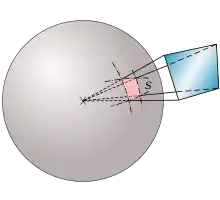
Dans le cas d'un cône de révolution de demi-angle au sommet ${\displaystyle \alpha }$, l'angle solide se calcule par intégration sur la sphère, dans les domaines angulaires des coordonnées sphériques :

${\displaystyle \Omega =\int \!\!\!\!\!\int \mathrm {d} ^{2}\Omega =\int _{0}^{2\pi }\mathrm {d} \phi \int _{0}^{\alpha }\sin \theta \ \mathrm {d} \theta \ =2\pi \int _{0}^{\alpha }\sin \theta \ \mathrm {d} \theta =2\pi \left[-\cos \theta \right]_{0}^{\alpha }\ }$,

${\displaystyle \Omega =2\pi \left(1-\cos \alpha \right)}$.

• Daniel Duverney, « Calcul différentiel et intégral pour la physique », sur touteslesmaths.fr
• Murray R. Spiegel (en), Analyse vectorielle, McGraw-Hill, 1973

• Diamètre apparent
• Géométrie euclidienne
• Géométrie dans l'espace
• Sinus polaire
• Trigonométrie sphérique
• Unité d'angle solide

• « Ibn Al-Haytham : l'angle solide comme grandeur » dans Roshdi Rashed, Angles et Grandeur : D'Euclide à Kamal al-Din al-Farisi, Walter de Gruyter GmbH & Co KG, 19 mai 2015 (ISBN 978-1-5015-0238-5, lire en ligne)