Nutation
La nutation est un mouvement périodique de l'axe de rotation d'un objet autour de sa position moyenne, qui s'ajoute à la précession.
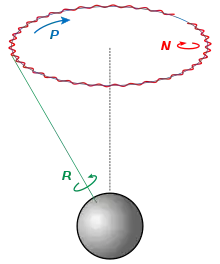
Nutation de la Terre
La nutation a été découverte en 1748 par l'astronome britannique James Bradley (1693-1762) en observant l'étoile Gamma Draconis (Eltanin) en vue de déterminer sa parallaxe.
En raison de l'attraction conjuguée du Soleil et de la Lune, la nutation se traduit par une oscillation de l'axe de rotation de la Terre pouvant aller jusqu'à plus ou moins 17,2″ (secondes d'arc) en longitude et à plus ou moins 9,2" en obliquité avec une période de 18,6 ans, qui est égale à celle de la précession du nœud ascendant de l'orbite lunaire. Le pôle vrai dessine alors autour du pôle moyen une ellipse dont le grand axe mesurant 9,21″ est dirigé vers le point vernal.
Classiquement, la nutation est composée de deux éléments :
- Nutation en longitude : décrivant l'oscillation du point vernal vrai autour du point vernal moyen. Au (0h), sa valeur angulaire était de -15,079" selon le modèle AIU80 ou, selon le modèle astronomique plus récent P03 recommandé par l'IMCCE et l'AIU en 2006, de -15,091".
- Au (0h), sa valeur s'inscrivait à -16,154" (AIU80) ou -16,162" (P03).
- Au (0h), sa valeur s'inscrivait à -14,339" (AIU80) ou -14,345" (P03).
- Au (0h), sa valeur s'inscrivait à -10,568" (AIU80) ou -10,571" (P03).
- Nutation en obliquité : décrivant l'oscillation de l'équateur vrai autour de l'équateur moyen. Au (0h), sa valeur angulaire était de -4,718" selon le modèle AIU80 ou, selon le modèle astronomique plus récent P03 recommandé par l'IMCCE et l'AIU en 2006, de -4,713".
- Au (0h), sa valeur s'inscrivait à 1,258" (AIU80) ou 1,265" (P03).
- Au (0h), sa valeur s'inscrivait à 4,075" (AIU80) ou 4,081" (P03).
- Au (0h), sa valeur s'inscrivait à 6,542" (AIU80) ou 6,549" (P03).
On observe que cette dernière valeur est bien en retrait des -9,2" de la valeur moyenne extrême de l'amplitude de la nutation en obliquité. Cela s'explique par le fait que, elle-même, l'obliquité moyenne de la Terre diminue continûment (actuellement de -0,468" par an) ; aussi une période de nutation a-t-elle une durée inférieure aux 18,6 années de la précession des nœuds. De plus, l'amplitude de la nutation passe par un maximum plus faible que +9,2" et un minimum plus élevé que -9,2". À titre d'exemple, considérons la période actuelle : la nutation était quasi nulle le (et nulle, à cette date, à 17h15'03,5"), maximale (+8,988") le , quasi nulle le , minimale (-9,583") le , et quasi nulle le (et nulle, à cette date, à 22h44'02"), soit sur une période de 18,29 ans (ou 18,51 ans en considérant les heures exactes indiquées pour les nutations exactement égales à zéro).
Les catalogues d'étoiles donnent habituellement les coordonnées astrométriques des étoiles. Celles-ci sont les coordonnées moyennes à une époque T fixée. Si l'on désire connaître les coordonnées vraies à une autre époque, il est impératif de corriger les coordonnées moyennes en tenant compte de l'effet de la précession sur la durée écoulée entre les deux époques. Il suffira ensuite de reprendre les coordonnées obtenues et de leur ajouter l'effet de la nutation.
Notes et références
Voir aussi
Bibliographie
- [Bradley 1748] (en) J. Bradley, « A Letter to the Right Honourable George Earl of Macclesfield concerning an Apparent Motion Observed in Some of the Fixed Stars » [« Lettre au très honorable George Earl de Macclesfield concernant un mouvement apparent observé dans certaines étoiles fixes »], Philosophical Transactions of the Royal Society, vol. 45, no 485, , p. 1-43 (DOI 10.1098/rstl.1748.0002, Bibcode 1748RSPT...45....1B).
- [Taillet, Villain et Febvre 2018] R. Taillet, L. Villain et P. Febvre, Dictionnaire de physique, Louvain-la-Neuve, De Boeck Sup., hors coll., , 4e éd. (1re éd. ), 1 vol., X-956, ill. et fig., 17 × 24 cm (ISBN 978-2-8073-0744-5, EAN 9782807307445, OCLC 1022951339, SUDOC 224228161, présentation en ligne, lire en ligne), s.v.nutation, p. 515, col. 1-2.