Précession des équinoxes
La précession des équinoxes est le décalage progressif de la direction où sont vues les étoiles, d'un siècle à l'autre, à raison d'une rotation complète, tous les 26 000 ans environ, effet produit par un lent changement de direction de l'axe de rotation de la Terre, dans la même durée.
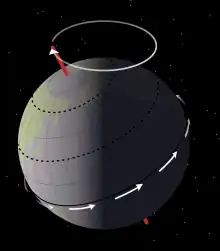

Ce phénomène avait déjà été remarqué dès les Babyloniens, mais il n'a été expliqué que par la compréhension des forces de marées qui s'exercent sur la Terre et par l’étude du mouvement des toupies par la mécanique du solide, au XVIIIe siècle.
Description du phénomène
Ce phénomène consiste en la variation de la direction de l'axe de rotation de la Terre selon un cycle d'environ 26 000 ans.
Il a été constaté dès l'Antiquité par les astronomes babyloniens sans que l'on puisse à l'époque en expliquer la cause.
Ce phénomène a notamment comme conséquence que d'un siècle à l'autre, à la même date et à la même heure, les étoiles ne sont pas vues dans la même direction. Plus précisément, le point vernal se déplace le long de l’écliptique d’environ 1 degré 23 minutes par siècle.
Ce changement de direction est provoqué par le couple qu'exercent les forces de marées de la Lune et du Soleil sur le renflement équatorial de la Terre. Ces forces tendent à amener l'excès de masse présent à l'équateur vers le plan de l'écliptique. La Terre étant en rotation, ces forces ne peuvent changer l'angle entre l'équateur et l'écliptique, mais provoquent un déplacement de l'axe de rotation de la Terre dans une direction perpendiculaire à cet axe et au couple (on trouvera une explication plus rigoureuse, ainsi qu’une démonstration mathématique, à l’article précession). En négligeant les petites perturbations agissant sur ce déplacement (par exemple, la nutation), l'axe de la Terre décrit la surface d'un cône ou « entonnoir » d'axe perpendiculaire sur le plan de l'écliptique (portant dans l'espace la trace de la trajectoire de la Terre autour du Soleil), à la manière de l'axe d'une toupie posée sur une table (qu'on voit tourner autour de la verticale).
Ce mouvement déplace l'orientation de l'axe des pôles par rapport aux étoiles et il en résulte que, au fil des millénaires, l'étoile polaire (repérant à peu près la direction du nord géographique) n'est plus toujours la même. Le mouvement de l'axe des pôles terrestres entraîne avec lui le plan de l'équateur (qui lui est perpendiculaire), et, par conséquent, le point vernal (ou point équinoxial, indiquant la direction du Soleil à l'équinoxe de printemps) précède chaque année sa position antérieure sur l'écliptique, par rapport au sens de l'orbite terrestre autour du Soleil. Pour cette raison, ce mouvement est appelé précession des équinoxes. Ainsi, le point équinoxial effectue, dans le sens inverse de la rotation de la Terre autour du Soleil, un tour complet de l'écliptique en 25 769 années environ, et durant ce même temps l'axe de la Terre décrit un cône complet.
Une des conséquences de ce déplacement est le changement de position des étoiles sur la sphère céleste dans le système de coordonnées équatoriales. En ce début de XXIe siècle, dans l'hémisphère Nord, l'étoile polaire (avec une minuscule), c'est-à-dire l'étoile brillante la plus proche du pôle Nord céleste, est α Ursae Minoris (m = 1,97), autrement appelée Polaris (la Polaire en latin), ou l'étoile Polaire (avec une majuscule). Dans le passé, vers 2800 av. J.-C., c'était l'étoile α Draconis (Thuban) qui servait d'étoile polaire, mais elle était beaucoup moins lumineuse que l'étoile Polaire. Par contre, dans environ 8 000 ans, Alpha Cygni (Deneb, 1,25m), puis dans environ 12 000 ans, la très brillante Alpha Lyrae (Véga, 0,03m), seront chacune à leur tour l'étoile polaire boréale, avec cependant un écart angulaire d'au moins 4 degrés. Dans l'hémisphère sud, il y a peu d'étoiles visibles à l'œil nu près du pôle céleste. L'étoile polaire australe actuelle est Sigma Octantis, autrement appelée Polaris Australis (la Polaire australe), de magnitude 5,5. Dans environ 13 000 ans, ce sera au tour d'Eta Columbae (m = 4) d'être au plus proche du pôle Sud céleste, dont elle est actuellement au plus éloigné.
Comme l'orbite de la Lune est inclinée par rapport au plan de l'écliptique, l'action de la Lune vient légèrement perturber la précession en y ajoutant de petites oscillations dont la période est de 18,6 ans. Cet effet s'appelle la nutation.
À cause de la précession des équinoxes, la durée du cycle des saisons (année tropique) est d'environ 20 minutes plus courte que la durée nécessaire à la Terre pour occuper la même position par rapport aux étoiles (année sidérale). Cette différence est importante pour les calendriers et leurs règles concernant les années bissextiles.
Selon le polynôme du 5e degré donné par Capitaine, Wallace et Chapron en 2003[2] pour la précession cumulée, la valeur au de la vitesse de précession (soit la première dérivée de la précession cumulée) était de 50,292 162 622 6 secondes d'arc par an, soit environ 1 degré tous les 71,58 ans et 360 degrés en 25 769,42 ans. Toutefois, la vitesse de précession n'est pas constante : actuellement, elle est légèrement croissante avec le temps (elle valait, par exemple, 50,287 961 95 secondes d'arc par an le et 50,290 172 84 secondes d'arc par an le , soit un accroissement (dit « séculaire ») de 0,022 108 696 seconde d'arc par siècle). Ce terme d'accroissement n'est cependant lui-même pas constant dans le temps : il croît très légèrement actuellement et varie avec une période d'environ 41 000 ans, la même durée que celle de la variation de l'obliquité de l'écliptique (un mouvement perpendiculaire à la précession), qui oscille entre 22° 2′ 33″ et 24° 30′ 16″, soit une amplitude de près de 2,5°. La valeur de l'obliquité « moyenne » au 1er janvier de l'an 2000 était de 23° 26′ 21,448″, selon le modèle de Laskar (1986), ou de 23° 26′ 21,406″, selon le modèle astronomique plus récent P03, recommandé par l'IMCCE et l'AIU depuis 2006 ; selon le premier modèle (Laskar1986), cette valeur était de 23° 26′ 12,555″ au 1er janvier 2019, ou de 23° 26′ 12,507″, selon le modèle plus récent P03 susmentionné ; elle continue de diminuer de 46,8 secondes d'arc par siècle. L'obliquité « vraie » est l'obliquité moyenne corrigée de la nutation en obliquité due à l'action de la Lune, avec une période 18,6 ans, oscillant entre +9,2″ et -9,2″ ; la nutation en obliquité valait -4,713″ en 2019, selon le modèle AIU2000 ; l'obliquité vraie au 1er janvier 2019 était donc de 23° 26′ 7,842″, selon Laskar 1986 et IAU2000, ou de 23° 26′ 7,795″, selon P03 et IAU2000. Cette diminution de 0,468 045 seconde d'arc par an a comme effet un déplacement annuel de quelque 14,5 mètres des tropiques vers l'équateur et des cercles polaires vers les pôles sur la surface de la Terre (la variation due à la nutation n'étant pas prise en compte, dont l'amplitude de ±291 m vers le nord et vers le sud couvre de loin cet effet qui ne devient effectif qu'au bout de 39 ans).
La valeur de l'obliquité moyenne était, en chiffres ronds, de 23° 30′ au 1er janvier de l'an 1533 (le modèle astronomique P03 donne très précisément 23° 29′ 59,909″ pour cette date, la valeur exacte de 23° 30′ 00,000″ ayant été atteinte, selon ce modèle, peu auparavant, soit le à 11 h 40). Dans une lettre de , l'astronome allemand Regiomontanus (Johannes Müller von Königsberg 1436-1476) reconnaît que les astronomes italiens Paolo Toscanelli (1397-1482) et Leon Battista Alberti (1404-1472) avaient déjà obtenu justement cette valeur lors de mesures annuelles faites durant les années 1440 à 1470 à Florence. Ces mesures ont été répétées avec une finesse accrue grâce au gnomon établi dès 1468 par Paolo Toscanelli à 90 mètres de haut dans la coupole (construite entre 1420 et 1436 par Filippo Brunelleschi) de la cathédrale Santa Maria del Fiore, permettant une remarquable précision de mesures de la hauteur du Soleil (et par conséquent de sa déclinaison) lors du solstice d'été à 2″ d'arc près, mesures possibles seulement entre le et le . Pourtant, en 1588, Tycho Brahe dans son De mundi aetheri recentioribus phaenomenis, donne encore 23° 30′ 30″, qui était précisément la valeur de l'obliquité 120 ans auparavant, soit le 18 juillet de l'an 1468 à 5 h 25, selon le modèle P03.
Histoire de la découverte
Le neuvième séminaire d'archéoastronomie organisé avec l'Observatoire Astronomique de Gênes, en Italie, le , a permis de faire le point des dernières découvertes concernant la mesure de l'équinoxe. La publication des actes montre que nos prédécesseurs avaient conçu dès la préhistoire des dispositifs permettant de mesurer l'équinoxe : (en) « We have found in Corsica examples of equinoctial alignments and we can demonstrate that it is possible at 45° of Latitude to obtain it by the perfect linear shadow of the stick, as in the Lascaux’s Grotto, Chantal Jègues has discovered the Vernal Point in the Scorpio and the Autumn One in the Taurus. »[3] Nos prédécesseurs démontrent qu'ils avaient les connaissances astronomiques pour comprendre et mesurer le phénomène : quelles que soient la latitude, la longitude et la déclinaison, et donc l'époque, le lever solaire d'équinoxe se fait toujours à l'azimut 90°[3].
Dans son livre Des Dieux, des tombeaux, des savants, l'archéologue C. W. Ceram signale que les astronomes babyloniens mentionnaient la précession des équinoxes même si, faute de modèle héliocentrique, ils n'en soupçonnaient pas la raison. Les astronomes babyloniens Nabu-rimanni (en 508 av. J.-C.) et Kidinnu (en 375 av. J.-C.) faisaient commencer leur zodiaque à respectivement 10° et 8° du point vernal alors qu'à leurs époques respectives la longitude sidérale (en considérant qu'Aldébaran se situait à 15° du signe du Taureau) du point vernal était réellement de 10° et 8° du Bélier[4]. Cependant, le phénomène de la précession était incompris des Grecs d'avant Hipparque, puisque tous recopièrent sans cesse des positions astronomiques périmées depuis longtemps[5].
On pense qu'Hipparque a découvert ce phénomène aux environs de 130 av. J.-C. En comparant ses mesures de la position de Alpha Virginis (Spica), une étoile proche de l'écliptique, par rapport au point vernal avec celles effectuées par les astronomes des siècles précédents, comme Timocharis d'Alexandrie et les astronomes babyloniens et chaldéens, il montra que le point vernal s'était déplacé de 2° par rapport à α Virginis. Il montra aussi que ce mouvement concernait aussi d'autres étoiles et valait au moins 1° par siècle[6].
On croit aussi que les Aztèques avaient calculé le cycle des 26 000 ans environ qui correspond à la précession[7].
Selon certains historiens, des civilisations antérieures à la Grèce antique connaissaient le mouvement de précession des équinoxes. Au début du XXe siècle, l'allemand Schnabel attribua la découverte du mouvement à l'astronome babylonien Kidinnu[8] - [9] et l'égyptologue René Adolphe Schwaller de Lubicz affirma que les anciens Égyptiens connaissaient cette précession. Ces affirmations sont cependant controversées[10]. Une certaine confusion entre le phénomène observé et son explication persiste. Même sans témoignage explicite, il est raisonnable d'admettre que là où s'est transmise la tradition d'observer le ciel nocturne, à la longue on a dû constater un certain décalage dans la position des étoiles proches de l'écliptique aux moments notables de l'année (solstices et/ou équinoxes). De même, si l'on s'est servi des étoiles éloignées des pôles pour orienter les monuments, après quelques siècles leurs alignements auront dévié. Toutefois, ces exemples ne permettent pas d'affirmer que la précession a été connue car différentes explications sont possibles : soit que le mouvement du ciel (s'arrête et) s'inverse, soit que seules les étoiles des constellations zodiacales, mais non toutes, se meuvent à la manière des planètes[11].
Au XIIIe siècle, Nasr Eddin Tusi avait calculé une valeur de 51″ par an pour la précession des équinoxes, ce qui est remarquable de précision.
Joseph-Alphonse Adhémar, James Croll et Milutin Milanković ont eu le mérite de proposer une correspondance entre ces cycles astronomiques et leurs combinaisons, et les variations climatiques terrestres (voir Paramètres de Milanković).
Mention dans la littérature
Dans La Machine à explorer le temps de H. G. Wells, l'observateur du temps mène sa machine en l'an 802701 et, contemplant le ciel étoilé, est surpris de penser que le cycle complet de précession ne s'est accompli en ce temps énorme que quelques dizaines de fois.
Notes et références
- (en) J. Vondrák, N. Capitaine et P. Wallace, « New precession expressions, valid for long time intervals », Astronomy & Astrophysics, vol. 534, , A22 (ISSN 0004-6361, DOI 10.1051/0004-6361/201117274, lire en ligne)
- (en) N. Capitaine, P. T. Wallace et J. Chapron, « Expressions for IAU 2000 precession quantities », Astronomy & Astrophysics, no 412, , p. 567-586 (lire en ligne)[PDF].
- (it) 9° Seminario di Archeoastronomia[PDF].
- Marie Delclos, Astrologie : Racines secrètes et sacrées, Éditions Dervy, (ISBN 978-2-85076-629-9), p. 179.
- Marie Delclos, op. cité, p. 157.
- Le livre d'Hipparque Περὶ τῆς μεταπτώσεως τῶν τροπικῶν καὶ ἐαρινῶν ἰσημερίων (Du changement des solstices et des équinoxes printanières) ne nous est pas parvenu. Nous en connaissons partiellement le contenu par l'intermédiaire de Ptolémée. Claude Ptolémée, Almageste, VII, trad. Nicolas Halma, 1813-1817.
- La grande encyclopédie de l'espace, 2002, p. 21.
- (de)Schnabel P., Berossos und die babylonisch-hellenistische Literatur, Leipzig-Berlin, Teubner, 1923.
- (en) Neugebauer O., The Alleged Babylonian Discovery of the Precession of the Equinoxes, J. Am. Oriental Soc., vol. 70 (1950), p. 1-8.
- Le moulin de Hamlet (1969 ; trad. 2011), un livre de Giorgio de Santillana et Hertha von Dechend, a proposé une relecture de toutes sortes de mythes comme l'expression archaïque de cette découverte. Robert Bauval et divers auteurs de pseudohistoires ont donné de nouveaux développements à ce sujet.
- Théon d'Alexandrie (IVe siècle) rapporte que des « astrologues anciens » auraient soutenu cette première contre-hypothèse, tandis que Hipparque lui-même aurait considéré (et rejeté) la seconde.
Voir aussi
Bibliographie
- Louis Poinsot, Précession des équinoxes, Machet-Bachelier, Paris, (lire en ligne)