Force de marée

Les forces d'attraction qu'exerce l'astre 1 sur les astres 2 et 3, notées F_1/2 et F_1/3, peuvent se décomposer en une composante moyenne F et une composante différentielle f_1/2 et f_1/3. Cette composante différentielle tend à éloigner les astres 2 et 3 (haut) ou à les rapprocher (bas).

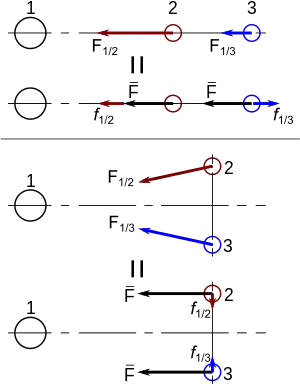
Imaginons deux masses d'un même côté d'un astre et alignées sur la direction de cet astre qu'on nommera par la suite « primaire » (mais qui n'est pas forcément le plus massif des trois), qui les attire. En vertu de la loi d'attraction universelle, la plus proche de l'astre sera plus attirée que l'autre et tendra donc à s'en séparer. Imaginons maintenant une autre configuration où la ligne qui joint les deux masses est perpendiculaire à la ligne qui va de leur centre de masse à l'astre. Les forces d'attraction ont des directions convergentes (vers l'astre) ; ainsi les masses auront une tendance à se rapprocher. Ainsi, l'astre primaire sera à la fois responsable du mouvement accéléré de l'ensemble des deux masses, plus précisément de leur centre de masse, mais aussi responsable de forces qui régissent le mouvement relatif de ces deux masses et qu'on appelle forces de marée. La force de marée est donc une interaction gravitationnelle indirecte entre ces masses induite par un ou plusieurs astres primaires.

L'expression exacte de cette force de marée sera dérivée plus loin. Le résultat essentiel, dans le cas le plus fréquent où une des masses, par exemple la Terre, est beaucoup plus grande que l'autre, par exemple une petite masse d'eau de l'océan ou un satellite de la Terre, et où la distance qui les sépare est beaucoup plus petite que la distance à l'astre primaire (la distance Terre-Lune par exemple), est que dans la configuration alignée cette force de marée est « centrifuge » et a pour intensité

${\displaystyle 2\mathrm {G} \,m\,\mathrm {M_{L}} r/\mathrm {R} ^{3}}$

où r est la distance de la masse d'eau au centre de la Terre, m la masse d'eau, R la distance Terre Lune (la Lune est l'astre primaire ici), ${\displaystyle \mathrm {M_{L}} }$la masse de la Lune, et G la constante universelle de la gravitation. Dans l'autre configuration envisagée, la force de marée est « centripète » et deux fois moins intense.

Cette force de marée, s'exerçant entre les constituants d'un satellite (dans ce cas, les deux masses considérées sont parties intégrantes d'un seul et même corps), tend à le déformer, voire parfois à le briser (voir la photographie de la brisure de la comète Shoemaker-Levy 9 par les forces de marée dues à Jupiter) lorsque la force de marée centrifuge l'emporte sur l'interaction gravitationnelle directe des deux parties ou sur les forces de cohésion de ces mêmes parties (voir ci-dessous la sous-section sur la limite de Roche).

Dans le cas où ce satellite a une rotation propre non synchrone avec sa révolution autour de l'astre, la déformation périodique qui en résulte est responsable des marées océaniques et/ou terrestres. De plus cette déformation périodique entraîne, par le biais des forces de friction, un échauffement du satellite. Ces forces de friction sont aussi à l'origine d'un couple qui tend à synchroniser sa rotation propre et sa révolution autour de l'astre, comme c'est déjà le cas pour la Lune qui nous montre toujours la même face. Ce même phénomène est également responsable du ralentissement progressif de la rotation de la Terre d'environ 2 ms/siècle. Ces forces de friction sont enfin responsables de la modification de l'orbite, le satellite pouvant s'écraser sur l'astre ou, au contraire, s'en éloigner comme c'est le cas pour l'orbite de la Lune qui s'éloigne d'environ 4 cm par an de la Terre.

Notons m₁ et m₂ les masses des objets soumis à marée et ${\displaystyle {\vec {\mathrm {F} }}_{1}}$ et ${\displaystyle {\vec {\mathrm {F} }}_{2}}$ les forces exercées par l'astre primaire sur chacune d'elles. L'étude du mouvement relatif se fait dans un référentiel centré au centre de masse des deux masses, noté CM, et dont les axes sont fixes par rapport aux étoiles. Le mouvement d'ensemble des deux masses est régi par la force résultante

${\displaystyle {\vec {\mathrm {F} }}_{1}+{\vec {\mathrm {F} }}_{2}}$

et son CM possède l'accélération

${\displaystyle ({\vec {\mathrm {F} }}_{1}+{\vec {\mathrm {F} }}_{2})/(m_{1}+m_{2})}$.

Ce référentiel n'est pas galiléen ; aussi à la force d'attraction, on doit ajouter la force d'inertie qui est l'opposé du produit de la masse par l'accélération. Ainsi la force de marée sur la masse 1 dans ce référentiel non galiléen est

${\displaystyle {\vec {\mathrm {F} }}_{\mathrm {t} }={\vec {\mathrm {F} }}_{1}-m_{1}{\frac {{\vec {\mathrm {F} }}_{1}+{\vec {\mathrm {F} }}_{2}}{m_{1}+m_{2}}}={\frac {m_{2}{\vec {\mathrm {F} }}_{1}-m_{1}{\vec {\mathrm {F} }}_{2}}{m_{1}+m_{2}}}=-{\frac {\mathrm {G} \,m_{1}m_{2}\mathrm {M} }{m_{1}+m_{2}}}\left({\frac {{\vec {r}}_{1}}{r_{1}^{3}}}-{\frac {{\vec {r}}_{2}}{r_{2}^{3}}}\right)=-{\frac {\mathrm {G} \,m_{1}\mathrm {M} }{1+m_{1}/m_{2}}}\left({\frac {{\vec {r}}_{1}}{r_{1}^{3}}}-{\frac {{\vec {r}}_{2}}{r_{2}^{3}}}\right)}$

avec l'indice t pour tide (marée en anglais), et l'expression opposée pour la masse 2. Dans la dernière expression[1], on a utilisé l'écriture de la force gravitationnelle sur la masse 1

${\displaystyle {\vec {\mathrm {F} }}_{1}=-\mathrm {G} \,m_{1}\mathrm {M} {\vec {r}}_{1}/r_{1}^{3}}$

où ${\displaystyle {\vec {r}}_{1}}$ est le vecteur qui part du CM de l'astre primaire et se termine au CM de la masse 1.

Dans la majorité des situations, le rapport m₁/m₂ est petit et c'est pourquoi ${\displaystyle 1+m_{1}/m_{2}\approx 1}$dans l'expression ci-dessus, ce qui fait disparaitre la masse m2 de l'expression. C'est le cas en particulier de la force de marée induite par la Lune entre la Terre (masse m₂) et une masse d'eau de l'océan (masse m₁) ou un fragment de la croûte terrestre ou un satellite artificiel de la Terre. Alors le centre de masse 1-2 est celui de la masse m₂ et on notera ${\displaystyle {\vec {r}}_{2}=-{\vec {\mathrm {R} }}}$ le vecteur qui va de l'astre primaire au CM de la masse lourde et ${\displaystyle {\vec {r}}}$ le rayon vecteur entre les deux masses, comme sur la figure. On posera

m₁ = m

et

${\displaystyle {\vec {r}}_{1}=-{\vec {\mathrm {R} }}+{\vec {r}}}$.

L'expression de la force de marée devient

${\displaystyle {\vec {\mathrm {F} }}_{\mathrm {t} }=-\mathrm {G} \,m\,\mathrm {M} \left({\frac {-{\vec {\mathrm {R} }}+{\vec {r}}}{(\mathrm {R} ^{2}-2\,{\vec {r}}{\vec {\mathrm {R} }}+r^{2})^{3/2}}}-{\frac {-{\vec {\mathrm {R} }}}{\mathrm {R} ^{3}}}\right)}$

On s'intéresse aux situations où r/R est très petit et où on peut utiliser le développement limité

${\displaystyle (1+\varepsilon )^{\alpha }=1+\alpha \,\varepsilon +\mathrm {O} (\varepsilon ^{2})}$ (α = -3/2), ce qui donne

${\displaystyle {\vec {\mathrm {F} }}_{\mathrm {t} }=-{\frac {\mathrm {G} \,m\,\mathrm {M} }{\mathrm {R} ^{3}}}\left((-{\vec {\mathrm {R} }}+{\vec {r}})\left(1+{\frac {3{\vec {r}}{\vec {\mathrm {R} }}}{\mathrm {R} ^{2}}}+\mathrm {O} ((r/\mathrm {R} )^{2})\right)+{\vec {\mathrm {R} }}\right)}$

Le premier terme non négligeable est la force de marée représentée en direction et intensité sur la figure[2]

${\displaystyle {\vec {\mathrm {F} }}_{\mathrm {t} }=-{\frac {\mathrm {G} \,m\,\mathrm {M} }{\mathrm {R} ^{3}}}\left({\vec {r}}-3\,{\vec {\mathrm {R} }}\left({\frac {{\vec {r}}{\vec {\mathrm {R} }}}{\mathrm {R} ^{2}}}\right)\right).}$

La force de marée induite par la Lune, astre primaire, qui régit le mouvement relatif du satellite S par rapport à la Terre est représentée en rouge en direction et en intensité par les flèches. Notons la symétrie par rapport au centre de la Terre.

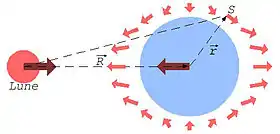
Évidemment, la force de marée exercée par la masse m sur M est l'opposée ; cependant ces forces n'ont pas le même support et elles engendrent un couple qui tend à aligner les trois astres. Notons, et ce n'est pas du tout intuitif, que les forces sont opposées pour deux points opposés de la masse M (par exemple l'un plus proche de l'astre primaire, l'autre plus loin du côté opposé ce qui explique le caractère semi-diurne de nos marées), et correspondent à des forces centrifuges maximales lorsque les trois masses sont alignées ${\displaystyle {\vec {r}}\cdot {\vec {\mathrm {R} }}=\pm r\mathrm {R} }$ d'intensité ${\displaystyle 2\mathrm {G} m\mathrm {M} r/\mathrm {R} ^{3}}$ et à des forces centripètes d'intensité deux fois plus faibles dans le plan équatorial à cette ligne c’est-à-dire ${\displaystyle {\vec {r}}\cdot {\vec {\mathrm {R} }}=0}$.

On peut reprendre pas à pas le même raisonnement dans le cas où il y a plusieurs astres primaires induisant une action gravitationnelle indirecte entre les masses 1 et 2 pour montrer que la force de marée totale est la somme vectorielle des forces de marée dues à chaque astre avec une intensité qui va comme le rapport M/R³ de chaque astre primaire. C'est ainsi que les forces de marées sur et au voisinage de la Terre, dues au Soleil représentent la moitié de celles dues à la Lune (le Soleil est situé beaucoup plus loin que la Lune mais sa masse est beaucoup plus importante).

Comme la Lune, les planètes et leurs satellites subissent des forces de marée, avec trois effets :

• évolution de la période de rotation du satellite, vers la période de révolution (ou vers une résonance spin-orbite différente de 1:1, quand l'orbite est suffisamment excentrique) ;
• évolution de la période de rotation de la planète, vers la période de révolution ;
• évolution de la distance planète-satellite : accroissement si la période de révolution est supérieure à la période de rotation de la planète, diminution dans le cas contraire.

On remarquera que les deux premières évolutions tendent vers un équilibre (synchronisation ou résonance), mais que la troisième s'éloigne de l'équilibre : si le satellite est plus éloigné que la distance à laquelle la période de révolution serait égale à la période de rotation de la planète, il s'éloigne encore plus (orbite super-synchrone) ; s'il est plus proche il se rapproche encore (orbite sous-synchrone).

Exemples :

• de nombreux satellites des planètes et des planètes mineures sont en rotation synchrone, dont la Lune, Phobos, Déimos et Charon ;
• la planète naine Pluton est en rotation synchrone (Charon et Pluton se présentent mutuellement toujours la même face) ;
• des deux satellites de Mars, l'un (Déimos) s'éloigne et sera sans doute perdu par Mars dans le futur, l'autre (Phobos) se rapproche et finira par s'écraser sur Mars (après s'être disloqué lors du passage par la limite de Roche).

Les forces de marée sont à l'origine de courants dans les liquides et de déformations dans les solides, auxquels s'opposent des frottements (surtout dans les liquides) qui engendrent un échauffement. On attribue à cet échauffement le volcanisme et plus généralement l'intense activité géologique de Io, un satellite de Jupiter dont on pense qu'il comporte un océan magmatique au-dessous de sa croûte silicatée.

Deux satellites d'une même planète peuvent exercer mutuellement des forces de marée. Les effets de ces forces mutuelles sont normalement plus faibles que ceux résultant des forces dues à la planète, mais ils peuvent leur être supérieurs en présence d'une résonance entre les périodes orbitales des deux satellites. C'est ce qui a été suggéré pour Io, Europe et Ganymède (trois des quatre satellites galiléens de Jupiter), en résonance 4:2:1 et sensibles aux marées en raison de la présence d'un océan d'eau sous la croûte de glace[6] - [7].

Comme une planète et l'un de ses satellites, le Soleil et l'une de ses planètes ou planètes mineures exercent mutuellement des forces de marée.

Exemples :

• sur Terre la marée d'origine solaire est nettement sensible, d'amplitude moitié moindre environ que celle d'origine lunaire ;
• sous l'effet des forces de marée d'origine solaire, Mercure a acquis une période de rotation en résonance 3:2 avec sa période de révolution.

Comme pour les satellites d'une même planète, les planètes du Système solaire exercent en principe des forces mutuelles de marée, mais elles sont extrêmement faibles. On a émis l'hypothèse que la quasi synchronisation dans un rapport 5:1 de la période synodique de Vénus (par rapport à la Terre, donc) et de son jour solaire était due aux forces de marée, mais il est plus probable que ce soit une coïncidence non permanente[8] - [9] - [10].

Le cas le plus spectaculaire est celui d’un objet en orbite proche autour d’un trou noir stellaire (ou encore d’une étoile à neutrons). La masse proprement astronomique du trou noir et sa petite taille autorisent un corps (une étoile ou une planète) à s’en approcher beaucoup et alors la différence de force gravitationnelle entre les deux faces de l’objet est gigantesque. Cet écart est tel que tout corps un tant soit peu volumineux est déchiqueté par la force de marée. C’est ce qui explique le commentaire qui accompagne toujours les descriptions de ce qui arriverait à un vaisseau spatial qui plongerait dans un trou noir stellaire : il serait détruit par les forces de marée avant même d’en avoir atteint l’horizon.

Cependant, à l’extérieur du trou noir, l’effet diminue au fur et à mesure que sa masse augmente. Dans le cas d’un trou noir galactique, dont la masse se mesure en millions de masses solaires, le rayon de l’horizon est suffisamment grand pour que la force de marée à ses environs soit sans danger pour un être humain qui se trouverait là.

En effet, l’amplitude des effets de marées subi par un corps de taille a situé à une distance d d’une masse M s’écrit comme le produit du gradient du champ gravitationnel par la taille de l’objet, soit :

${\displaystyle g_{\mathrm {m} }\simeq {\frac {\mathrm {G} \mathrm {M} a}{d^{3}}}}$

où G est la constante de Newton. Pour un être humain (où a vaut de l’ordre d’un mètre), la valeur maximale de g_m supportable est de l’ordre de l’accélération de la pesanteur terrestre g ; cela correspond à une situation où une personne suspendue par les mains serait lestée d’une masse de l’ordre de 100 kilogrammes, au-delà, elle serait écartelée. Cela correspond donc à la contrainte :

${\displaystyle {\frac {\mathrm {M} }{\mathrm {M_{T}} }}<{\frac {d^{3}}{a\mathrm {R_{T}} ^{2}}}}$

où M_T et R_T correspondent à la masse et le rayon de la Terre.

Pour un trou noir, la taille R de l’horizon est donnée approximativement par la formule

${\displaystyle \mathrm {R} \simeq {\frac {\mathrm {G} \mathrm {M} }{c^{2}}}}$.

Pour un observateur traversant l’horizon (d = R), la contrainte devient :

${\displaystyle \mathrm {M} >{\frac {c^{3}}{\mathrm {G} }}{\sqrt {\frac {a}{g}}}}$

soit de l’ordre de la centaine de milliers de masses solaires. Pour un trou noir plus massif, comme un trou noir galactique, il est donc possible de passer l’horizon sans dommage.