Marée
La marée est la variation de la hauteur du niveau des mers et des océans, causée par la combinaison des forces gravitationnelles dues à la Lune et au Soleil et des forces d'inertie dues à la révolution de la Terre autour du centre de masse du couple Terre-Lune et de celui du couple Terre-Soleil, le tout conjugué à la rotation de la Terre sur son axe.
Lors de la pleine lune et de la nouvelle lune, c'est-à-dire lorsque la Terre, la Lune et le Soleil sont sensiblement dans le même axe (on parle de syzygie), l'influence des corps célestes s'additionne et les marées sont de plus grande amplitude (vives-eaux). Au contraire, lors du premier et du dernier quartiers, lorsque les trois corps sont en quadrature, l'amplitude est plus faible (mortes-eaux)[1].
Le courant de marée montante se nomme flux ou flot, le courant de marée descendante se nomme reflux ou jusant[2].
Selon l'endroit de la Terre, le cycle du flux et du reflux peut avoir lieu une fois (marée diurne) ou deux fois par jour (marée semi-diurne)[3] ou encore être de type mixte.
Le niveau le plus élevé atteint par la mer au cours d'un cycle de marée est appelé pleine mer (ou couramment marée haute). Par opposition, le niveau le plus bas se nomme basse mer (ou marée basse). Lorsque la mer a atteint son niveau le plus haut ou le plus bas et semble ne plus progresser, on dit que la mer est étale. Parler de « marée haute » et de « marée basse » est le plus courant, bien que le mot marée désigne normalement un mouvement.
Les marées les plus faibles de l'année se produisent normalement aux solstices d'hiver et d'été, les plus fortes aux équinoxes de printemps et d'automne.
Ce mouvement de marée est le plus visible, mais il n'est pas limité aux eaux : des marées, presque invisibles, affectent aussi l'atmosphère (marées atmosphériques) et toute la croûte terrestre (marées terrestres), bien que dans une moindre mesure. Par conséquent, ce que nous percevons sur les côtes est en fait la différence entre la marée crustale et la marée océanique. Plus généralement, en raison des lois de la gravité, les objets et fluides célestes sont l'objet de forces de marée à proximité d'autres corps (Io, satellite rapproché de Jupiter, est soumis à des forces de marée colossales).


Origine
Les marées sont dues à la déformation des océans par les forces d'attraction de la Terre et des corps célestes les plus influents (la Lune et le Soleil). Elles s'expriment de façon différente en chaque point du globe, en raison de nombreux effets additionnels : inertie du déplacement de l'eau, effets induits par la marée elle-même et les déformations terrestres, propagation des ondes différentes induites par des facteurs tels que la force de Coriolis, la taille et la forme des bassins (ouverts ou fermés, profond ou pas), etc.[4].
Théorie de la marée
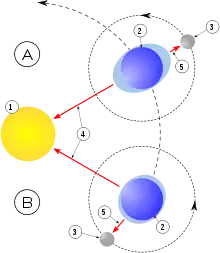
A. Syzygie ; B. Quadrature
1. Soleil ; 2. Terre ; 3. Lune
4. Direction de l'attraction par le Soleil
5. Direction de l'attraction par la Lune.
Selon la loi universelle de la gravitation, les masses liquides des mers et des océans sont attirées par les objets célestes les plus influents : la Terre, la Lune et le Soleil. En particulier, le point le plus proche de la Lune est plus attiré que le point à l'opposé. Une première composante de la force de marée résulte donc de la différence d'attraction entre celle de la Terre et de celle de la Lune, selon le barycentre Terre-Lune.
Le même phénomène existe pour l'ensemble des astres, et en particulier pour le Soleil, qui, bien qu'éloigné de la Terre, exerce une forte influence en raison de sa masse élevée.
D'autre part, la Terre tourne autour du barycentre du système Terre-Lune[5], ce qui soumet les objets situés à sa surface à une force centrifuge. De façon simplifiée, la marée résulte donc de la combinaison de ces deux forces :
- la force résiduelle résultant de la combinaison des différentes forces d'attraction ;
- une force centrifuge due à la rotation du système Terre-Lune[4].
C'est la combinaison de ces deux facteurs qui explique la présence de deux « bourrelets d'eau » de part et d'autre de la Terre selon l'axe Terre-Lune[4].
Il s'ensuit une déformation de la surface des mers, mais aussi des sols, qui diffère donc de ce qu'elle serait sans la présence de la Lune et du Soleil.
Pour la mer, on peut comparer cette déformation à une énorme vague qui serait de forme régulière si les fonds des océans « étaient réguliers et s'il n'y avait pas de côtes ».
Il convient d'ajouter que la rotation diurne de la Terre sur elle-même n'est pas à l'origine physique — au sens strict — du phénomène de marée. En revanche, elle participe au phénomène en ce que la rotation vient localement moduler l'effet de la marée, un même lieu du globe voyant un potentiel générateur variant dans le temps du fait de la combinaison du mouvement de rotation et des mouvements relatifs des corps perturbateurs par rapport à la Terre.
Potentiel générateur
La présence de la Lune et du Soleil est à l'origine de forces de gravitation qui produisent les marées.
La force génératrice de la marée dérive d'un potentiel lié à la distance de la Terre à la Lune, soit environ 380 000 km, alors que le rayon de la Terre est environ 6 400 km. L'attraction que subit une particule en un point quelconque du globe diffère en amplitude en fonction de sa position.
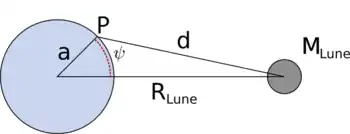
Notons le potentiel dont dérive la force génératrice de la marée. Dans un repère géocentrique on écrit ce potentiel appliqué à un point P de la surface du globe, affecté des coordonnées sous la forme :
(eq : 1.1)
avec :
- la constante de gravitation
- la masse du corps céleste perturbateur
- la distance entre le point et le centre du corps céleste perturbateur
- la distance entre le centre de la Terre et celui du corps céleste perturbateur
- le rayon de la Terre
- l'angle zénithal du corps céleste perturbateur au point
On peut exprimer en fonction de , et par la relation issue du théorème d'Al-Kashi (voir figure représentation Terre-Lune) :
(eq : 1.2)
si on exprime 1/d, l'équation précédente (eq 1.2) devient :
(eq : 1.3)
La Lune et le Soleil sont les seuls corps célestes dont l'influence est notable dans la génération des marées sur la Terre, l'un en raison de sa proximité, l'autre en raison de sa masse.
Le terme vaut environ pour la Lune et pour le Soleil. On peut donc estimer que :
Il devient donc possible, avec cette supposition, de décomposer (eq 1.3) sous la forme d'une série en à l'aide de polynômes de Legendre.
avec les polynômes de Legendre définis par :
C'est là qu'intervient une subtilité. Le terme principal de la série est celui d'ordre 1, qui est proportionnel à . Ce terme a une période angulaire de 360 degrés, ce qui signifie qu'il décrit un cycle de basse - pleine mer en 24 heures. Or le cycle des marées est d'environ 12 heures. Pour résoudre cette question, il convient de préciser que le référentiel dans lequel on analyse le problème n'est pas galiléen, car la Terre et la Lune ne sont pas immobiles (comme montré dans la figure), mais elles sont en rotation autour de leur centre de gravité commun. L'analyse rigoureuse des forces oblige donc à ajouter au potentiel décrit par (eq 1.1) un terme de potentiel décrivant la force d'entraînement de notre référentiel (qui est en l’occurrence une force centrifuge) pour pouvoir appliquer les lois de la mécanique. Or ce terme centrifuge compense et annule exactement le terme d'ordre 1 de la série. Le terme le plus grand de la série devient alors celui d'ordre 2.
Si on se limite à l'ordre 2 qui représente déjà 98 % du signal[6], on peut écrire le potentiel (eq 1.1) sous la forme :
(eq : 1.4)
On donne les coordonnées au corps céleste et les coordonnées au point du globe P, on peut donc exprimer sous la forme :
L'équation (eq 1.4) devient alors :
Si on détaille chacun des trois termes de l'équation (eq 1.5), et que l'on ne considère que le mouvement de rotation de la Terre en un jour, nous pouvons obtenir les termes de génération des premières ondes de marée.
En effet :
- Le terme effectue deux périodes lors d'une rotation de l'angle de (rotation de la Terre en 1 jour), il décrit donc une fonction semi-diurne ;
- Le terme n'effectue qu'une période lors d'une rotation, il décrit donc une formule diurne ;
- Enfin le terme ne dépend pas de la longitude mais uniquement de la latitude du corps céleste et du point de mesure, ce terme varie en fonction du mouvement de déclinaison du corps céleste (période 24 h), il décrit donc une fonction longue période.
Nous ne développerons pas davantage ici le potentiel en fonction de tous les mouvements orbitaux des deux corps célestes perturbateurs. Nous ne citerons que les travaux de l'astronome et mathématicien George Darwin, deuxième fils du célèbre biologiste Charles Darwin.
- En 1883, il a effectué ce précédent calcul et a extrait 59 termes solaires et 32 termes lunaires. Ce travail est repris par Doodson qui a déduit près de 400 termes et plus récemment par bien d'autres chercheurs notamment Schureman en 1958.
Ce sont George Darwin et Doodson qui ont nommé les termes du développement du potentiel, ces noms sont toujours utilisés pour nommer les ondes.
Les noms correspondent à un assemblage d'informations, ainsi M vient de M (Moon) un terme lunaire et 2 un terme semi-diurne, il en est de même pour l'onde solaire S.
Pourquoi deux bourrelets opposés ?

Prenons deux objets sphériques homogènes A et B attirés l'un vers l'autre par la force gravitationnelle. Pour l'objet A, son centre de gravité est attiré vers le centre de gravité de B, selon les lois de l'attraction universelle (g sur le schéma). La force d'attraction est un peu plus importante sur la partie la plus proche de B (g + sur le schéma), cette partie va donc avoir tendance à se bomber en direction de B, car la force d'attraction y est plus importante que celle au centre de gravité de A. Par contre, sur la partie de A la plus éloignée de B, l'attraction est moins forte (g - sur le schéma), la force d'attraction y est plus faible, et cette partie éloignée va avoir tendance à se bomber dans la direction opposée à B. La rotation de la Terre et de la Lune s'effectue autour du centre de gravité commun de l'ensemble Terre-Lune (qui se situe à l'intérieur de la Terre, à 4 700 km de son centre). Sous les hypothèses ci-dessus de la marée statique, on observerait typiquement deux marées océaniques correspondant à chacun des deux bourrelets situés sur la droite Terre-Lune. Comme la Terre tourne sur elle-même, le phénomène s'observerait suivant une périodicité semi-diurne d'environ 12 h 25 min, correspondant à la moitié du jour lunaire (temps séparant deux passages successifs de la Lune au méridien). Une périodicité de 12 h pourrait aussi être relevée, ce qui traduit l'existence d'une marée solaire, d'amplitude un peu moins forte que celle causée par la Lune.
Toutefois, le raisonnement présenté ne prend pas en compte les effets de propagation horizontale des courants de marée à la surface des océans, ou à proximité des côtes. Il en résulte dans ce dernier cas l'existence de marées de grande amplitude dans certaines régions propices, par la conformation des rivages ou des fonds, et dans le premier cas l'existence dans certaines régions océaniques de points où on n'observe qu'une seule marée journalière.
La Lune subit aussi un effet de marée causé par la Terre, et beaucoup plus important que celui observé sur Terre, compte tenu de la masse importante de la Terre par rapport à la Lune. C'est pourquoi petit à petit le mouvement de rotation de la Lune sur elle-même s'est synchronisé au mouvement de la Lune autour de la Terre, nous présentant désormais toujours la même face (à une petite oscillation près : la libration). La Lune subit de la part de la Terre un effet de marée constant à sa surface, ce qui explique que sa forme ne puisse pas être parfaitement sphérique, mais ellipsoïdale.
Les effets de marée existent aussi sur la croûte terrestre, qui se soulève au passage de la Lune et du Soleil et aux antipodes. Le développement d'une théorie systématique des marées terrestres a débuté avec George H. Darwin en 1879[7] et a ensuite été poursuivi par de nombreux auteurs, notamment par William Kaula en 1964[8] et par Paul Melchior[9]. C'est cet effet qui a permis de résoudre une énigme au CERN, dans les relevés effectués au LEP : les faisceaux de particules faisaient un trajet plus long à cause de ce soulèvement avec un rythme identique à celui des marées. Cette différence de trajet modifiait périodiquement les mesures. On parlait d’une amplitude de 40 cm de déplacement vertical de la croûte terrestre[10], pas très différent de l'amplitude moyenne du mouvement moyen au centre des océans.
Autres effets induits : ralentissement de la vitesse de rotation de la Terre, et éloignement de la Lune
Le phénomène des marées crée des mouvements de la structure terrestre et des océans qui engendrent des frottements, soit une dissipation d’énergie (sous forme de chaleur) qui est prélevée sur l’énergie cinétique de rotation de la Terre.
Dans le même temps, afin de conserver le moment cinétique du système Terre-Lune, la Lune s'éloigne de la Terre d'environ 3,8 centimètres par an[4] - [11] - [12].
Ces mécanismes contribuent l'un et l'autre à une réduction de l’énergie cinétique, soit un ralentissement de la vitesse de rotation de la Terre qui entraîne un rallongement de la durée des jours[4]. Durant les 100 derniers millions d’années, on estime que la durée de la journée a augmenté d’une heure. Actuellement, la durée d’une journée augmente d'environ 2 ms par siècle.
Grandes marées
Le passage de la Lune au méridien du lieu (éventuellement avec un certain retard dans les oscillations forcées ; on appellera « méridien de marée » le méridien qui correspond à l'angle horaire de retard des marées) ou à opposition explique le cycle semi-diurne. La période de ce phénomène est 0,517525050 jour (12 heures 25 minutes 14 secondes), moitié de la durée du jour lunaire moyen. La différence de temps (le retard), pour un port donné, entre le passage de Lune au méridien et l'heure de la pleine mer est appelé établissement du port[13]. Les grandes marées se produisent habituellement à l'automne et au printemps[14].

Plusieurs phénomènes astronomiques contribuent à la variation de l'amplitude des marées :
- la syzygie du Soleil et de la Lune (autrement dit, la nouvelle ou pleine lune). Cela se produit essentiellement lorsque la longitude du Soleil et de la Lune sont voisines ou voisines de l'opposition l'une de l'autre, soit deux fois par mois. Précisément, la période de ce phénomène est 14,7652944 jours, moitié de la durée que l'on qualifie de mois lunaire synodique ;
- le passage du Soleil au nœud lunaire, c'est-à-dire le passage du Soleil dans le plan de l'orbite lunaire : celui-ci se produit deux fois par an (à la régression du nœud près), et détermine les « saisons d'éclipses » (ce sont pendant celles-ci que les éclipses de Soleil ou de Lune se produisent). Les marées sont alors plus importantes en syzygie (voir le point précédent) en raison du meilleur alignement Terre-Lune-Soleil. La période précise est 173,310038 jours, moitié de la durée que l'on qualifie d'année draconitique. Le passage du Soleil au nœud lunaire s'est par exemple produit le , le , le , le (plus précisément, cela sont les dates de coïncidence des longitudes moyennes ; notamment, le calcul des anomalies est omis ; mais on reconnaît le voisinage de l'éclipse de Lune du et de l'éclipse de Soleil du 21 juin 2001). Comme on le constate, ces dates sont actuellement proches des solstices mais évoluent rapidement dans l'année au cours du temps ;
- le passage du Soleil dans le plan équatorial, qui se fait aux équinoxes, donc deux fois par an. La période précise est 182,621095 jours, la moitié d'une année tropique. Le phénomène des marées d’équinoxes n’a rien à voir avec l’alignement Lune-Terre-Soleil, qui a lieu toutes les deux semaines à la pleine lune et à la nouvelle lune et se réalise d’autant mieux lorsqu’il coïncide avec le cycle draconitique de 173 jours (Éclipse#Principes mécaniques). Le Soleil se trouve au-dessus de l’Équateur lors des équinoxes, alors qu’il est au-dessus du tropique du Cancer lors du solstice de juin et au-dessus du tropique du Capricorne lors du solstice de décembre. Rappelons que l’effet de marée d’un astre est maximal au point de la Terre se trouvant le plus proche de cet astre et au point se trouvant le plus éloigné. Aux moments des solstices, un des points où l’effet de marée du Soleil est maximal se trouvera en permanence sur le tropique du Cancer, pendant que l’autre se trouvera aux antipodes, sur le tropique du Capricorne. Chaque point se trouvant sur un des deux tropiques sera donc soumis à un effet de marée maximal du Soleil une seule fois par jour (on parle d’onde diurne). Au moment des équinoxes, ces deux points seront en permanence sur l’Équateur. Chaque point de l’équateur sera donc soumis à un effet de marée maximal du Soleil deux fois par jour (on parle d’onde semi-diurne). À ce moment-là, le terme diurne s'annule dans le calcul des marées, et le terme semi-diurne est maximal ;
- le passage de la Lune au périgée, moment auquel les forces de marée exercées par la Lune sont donc les plus importantes. À la différence du nœud lunaire, qui régresse sur l'écliptique, le périgée, lui, avance. Le temps entre deux passages de la Lune au périgée est le mois anomalistique, de 27,5545499 jours. Le calcul de la position du périgée lunaire est soumis à énormément de perturbations ;
- le passage de la Terre au périhélie, moment auquel les forces de marée exercées par le Soleil sont donc les plus importantes. Le périhélie terrestre progresse sur l'écliptique ; cela dit, la majeure partie (environ 5/6e) de cette progression est en réalité due à la régression (« précession ») de l'équinoxe par rapport aux étoiles fixes. Le temps séparant deux passages de la Terre au périhélie est l'année anomalistique de 365,259636 jours. Il se produit actuellement le de l'année.
Il est possible d'avoir des conjonctions entre tous ces phénomènes, conduisant à des marées exceptionnellement importantes, ou au contraire des annulations partielles conduisant à des marées de faible amplitude.
Marées extraterrestres
Comme le système Terre-Lune, les systèmes planète-satellite et Soleil-planète, voire satellite-satellite et planète-planète, sont le siège de forces de marée. On leur attribue notamment :
- la rotation synchrone de nombreux satellites, dont la Lune, Phobos, Déimos et Charon ;
- l'éloignement progressif de certains satellites (dont la Lune et Déimos) et le rapprochement d'autres (dont Phobos) ;
- la rotation synchrone de Pluton ;
- la résonance spin-orbite de Mercure ;
- l'intense activité géologique de Io.
Les effets des forces de marée sont particulièrement spectaculaires au voisinage d'un trou noir ou d'une étoile à neutrons.
Autres facteurs influant sur les marées
Pour la Terre, seuls la Lune et le Soleil ont des impacts significatifs, qui s'additionnent ou se contrarient selon les positions respectives de la Terre, de la Lune et du Soleil, et de leur inclinaison. En fait, la Lune est beaucoup plus proche de la Terre que le Soleil, mais a aussi une masse beaucoup plus petite, de telle sorte que leurs attractions sont d'ordres de grandeur comparables : celle du Soleil est environ la moitié de celle de la Lune. Les autres corps célestes possèdent un rapport masse/distance trop faible pour que leur influence soit sensible.
Cette attraction combinée de la Lune et du Soleil est cependant perturbée ou même parfois contrariée par d'autres phénomènes physiques comme l'inertie des masses d'eau, la forme des côtes, les courants marins, la profondeur des mers, ou encore le sens du vent local.
De plus, un cycle long s’établit aussi sur une période de 18,6 ans durant lequel le niveau moyen des pleines mers augmente de 3 % par an durant 9 ans, puis diminue de 3 % durant 9 ans, et ainsi de suite. Ce cycle exacerbe puis diminue les effets de la montée des océans induite par le réchauffement climatique[15] Selon l'IRD de France, là où l'amplitude des marées est naturellement forte (exemple : baie du Mont Saint-Michel) ce cycle contribuera dans les années 2008-2015 proportionnellement plus à l'élévation du niveau de la pleine mer, ou des grandes marées hautes que le seul réchauffement climatique (jusqu'à + 50 cm, c'est-à-dire 20 fois l'expansion thermique de l'océan consécutive au réchauffement climatique global). Inversement de 2015 à 2025 la phase décroissante de ce cycle devrait conduire à un ralentissement apparent du phénomène de montée de l'océan, et probablement de l'érosion du trait de côte qui lui est généralement lié.
L'inertie
C'est une force qui s'oppose au mouvement d'une masse que l'on veut déplacer (augmentation de vitesse) ou arrêter (diminution de vitesse). Plus la masse est grande, plus l'inertie sera importante. C'est le cas de la masse d'eau de tous les océans du globe, qui tente de contrarier les mouvements auxquels elle est soumise par attraction combinée de la Lune et du Soleil.
Il y a généralement deux cycles de marée par jour (il y a des exceptions) dont les instants de haute mer et de basse mer varient avec la Lune (attraction prépondérante).
La marée se manifeste essentiellement sur les côtes maritimes, où la mer monte ou se retire suivant un cycle lié, d'une part à la rotation de la Terre et à sa révolution autour du Soleil, d'autre part à la rotation de la Lune autour de la Terre. Ce cycle complet (pleine et basse mer) dure environ 12 heures 25 minutes.
L'effet piston
Lorsque les côtes se resserrent en entonnoir, comme dans le fond de certaines baies (baie du Mont-Saint-Michel, baie de Fundy, etc.) il y a amplification de la hauteur des marées qui peuvent dépasser 14 mètres entre les basses eaux et les hautes eaux par effet de résonance. Il s'y produit aussi un retard horaire progressif comme en Manche de l'entrée à Dunkerque, ou dans l'estuaire du fleuve Saint-Laurent au Canada. Les mers intracontinentales et intérieures sont peu sujettes aux marées car les masses d'eau et les distances entre les côtes concernées sont beaucoup plus faibles que dans les océans. Pour les mers partiellement ouvertes, tout dépend de l'ouverture par rapport au volume propre : en Méditerranée, l'étroitesse du détroit de Gibraltar empêche remplissage ou vidage conséquent, alors que dans le golfe du Morbihan, la marée génère des courants violents.
Les marées terrestres
Le susbstrat géologique et la croûte terrestre subissent aussi l'influence des marées. En effet les plaques formant le manteau terrestre sont épaisses et solides, mais tout en étant assez élastiques et déformables à grande échelle, et de ce fait se déplacent comme le niveau des océans, mais la déformation de la terre est moindre (de l'ordre d'un à quelques décimètres)[4] que celle des grandes masses marines. À Paris, aux heures qui correspondraient à une pleine mer, le niveau terrestre est ainsi plus éloigné du centre de la Terre d'environ 30 centimètres en comparaison avec une position par rapport à la Lune correspondant à une basse mer. Les marées terrestres, combinées à l'auto-gravitation de la masse océanique, tendent d'autre part à réduire le marnage en pleine mer (correspondant à la marée d'équilibre) d'environ 30 %.
Les marées terrestres sont capables de déclencher des tremblements de terre de forte magnitude[16].
Historique de l'étude des facteurs causaux des marées
De l'Antiquité au VIe siècle
Dans l'Antiquité, le phénomène de marée est remarqué par Hérodote dans la mer Rouge, et les Grecs avaient également noté les courants capricieux de certains détroits méditerranéens. Ils prirent pleinement conscience du phénomène en s'aventurant en dehors de la Méditerranée, au IVe siècle av. J.-C. (Pythéas en Atlantique, Alexandre le Grand en Inde). Un lien avec la position de la Lune est proposé par le même Pythéas[17], celui-ci se fondant sur ses propres observations ainsi que sur celles des Celtes de la côte Atlantique.
Platon pensait que les marées étaient provoquées par des oscillations de la Terre. Mais les observations les plus précises sont effectuées par Posidonios au Ier siècle av. J.-C. à Cadix. Il décrit trois phénomènes périodiques liées aux marées[18] : les deux marées quotidiennes, correspondant aux deux culminations (inférieure et supérieure) de la Lune ; la période semi-mensuelle correspondant aux syzygies avec le Soleil ; la période semi-annuelle correspondant aux marées d'équinoxe. Il évalue correctement le décalage entre le passage de la Lune et le soulèvement des eaux.
Posidonios voit dans ce phénomène la manifestation d'une sympathie, d'une attirance des flots pour la Lune réputée humide. Cicéron, Pline l'Ancien[19], Strabon, Ptolémée affirment que le phénomène des marées dépend des cours de la Lune et du Soleil.
Du VIIe au XVIIIe siècle
Au VIIe siècle, avec Augustin Erigène, les termes de morte-eau (ledo) et de vive-eau (malina) et leur corrélation avec les phases de la Lune apparaissent pour la première fois[20].
Au VIIIe siècle, Bède le Vénérable approfondit les observations de Posidonios et étudie les variations des marées d'un point à l'autre de la côte anglaise[21]. Il est le premier à « affirmer l'existence et la constance, en chaque lieu, d'un retard de la marée sur l'heure lunaire »[22] : l'établissement du port. Il constate que « des vents favorables ou contraires peuvent avancer ou retarder les heures du flux et du reflux... »[22].
Au IXe siècle, l'astronome perse Albumasar décrit de façon détaillée dans son Introductorium magnum ad Astronomiam les corrélations entre marée et Lune[23].
Toutefois, si l'explication par l'attirance a la faveur des astrologues et des médecins pour qui la Lune est l'astre humide par excellence[24], elle n'est pas reçue par les disciples d'Aristote qui limitent à la lumière et au mouvement l'action des astres sur la Terre.
À partir du XIVe siècle, se développe la théorie aimantique des marées qui compare l'action de la Lune sur les eaux de la mer à l'action de l'aimant sur le fer.
C'est aux médecins et astrologues du XVIe siècle qu'il faut attribuer l'idée de décomposer la marée totale en deux marées de même nature, l'une produite par la Lune, l'autre par le Soleil[25].
Au XVIIe siècle, Kepler adopte le concept d’une force d’attraction de la Lune, de nature magnétique, qui engendrerait le phénomène des marées[26]. Galilée se moque de la position de Kepler quant à l'attraction lunaire[27] et explique le flux et le reflux de l’océan par les actions qu‘engendre la rotation de la Terre. Malgré les objections[28], Galilée considère prouver le mouvement de la Terre par cette explication.
La théorie de la gravitation de Newton permit de revenir à l'influence lunaire et solaire, fondée sur des principes scientifiques. Cette théorie fut largement adoptée au cours du XVIIIe siècle, même si, au début du XIXe siècle, Bernardin de Saint-Pierre tenta de persuader l'Académie des sciences française que ce n'était pas la Lune mais la fonte (alternée avec le gel nocturne) des glaciers qui provoquait les marées. Poussant jusqu'au bout son raisonnement, il justifiait la grande amplitude des marées d'équinoxe par l'action conjuguée des glaciers arctiques et antarctiques.
Marnage
Le marnage est, pour un jour donné et dans un intervalle pleine mer - basse mer, la différence de hauteur d'eau entre le niveau de la pleine mer et celui de la basse mer (exemple : marnage de 6,0 m). Le marnage varie continuellement.
La zone alternativement couverte et découverte par la mer, limitée par ces deux niveaux lorsqu'ils sont à leur maximum, est appelée l'estran ou zone de marnage, ou encore « zone de balancement des marées ».
Le marnage est parfois confondu avec l'amplitude de marée, mais cette dernière expression est tantôt assimilée à l’expression anglaise tidal range désignant le marnage[29], tantôt assimilée à l’expression tide amplitude désignant le demi-marnage (différence de hauteur d'eau à pleine mer ou à basse mer avec celle de la mi-marée)[30].
Coefficient de marées
Il s'exprime en centièmes et varie de 20 à 120, et indique la force de la marée. Le coefficient moyen est 70.
Les grandes marées ou marées de vives-eaux se produisent lorsque la Lune et le Soleil se trouvent en conjonction ou opposition (on parle de syzygie) par rapport à la Terre (situation de pleine ou de nouvelle lune) : leurs forces d'attraction s'ajoutent. Ce phénomène explique que les plus grandes marées (marées d'équinoxes) ont lieu lors de la première syzygie qui suit l'équinoxe ( et ).
Inversement, les marées sont faibles (marées de mortes-eaux) lorsque la Lune est à 90° de l'axe Soleil-Terre (situation de premier ou dernier quartier). De même, les plus faibles ont lieu aux alentours des solstices d'été et d'hiver ( et ).
- C = 20, définit la plus faible marée possible
- C = 45, définit une morte-eau moyenne
- C = 70, définit la séparation entre vive-eau et morte-eau
- C = 95, définit une vive-eau moyenne
- C = 100, définit une vive-eau équinoxiale moyenne
- C = 120, définit la plus forte marée possible
Si U est, en un lieu donné, le demi-marnage de la plus forte marée de vive-eau survenant après une syzygie équinoxiale moyenne (C = 100), alors la hauteur d'eau (h) à la pleine mer d'une marée de coefficient (C) est environ :
- hpm = (1,2 + C) × U
- de même la hauteur d'eau à la basse mer sera approximativement : hbm = (1,2 − C) × U
Note :
- Dans ces deux précédentes formules, le coefficient C ne doit pas être exprimé en centièmes. C variant de 20 à 120, dans ces formules il prendra les valeurs de 0,2 à 1,2.
- U est également appelé unité de hauteur du lieu considéré.
Exemple pratique : la hauteur d'eau à pleine mer en un lieu où l'unité de hauteur U = 5,50 m, lorsque le coefficient C = 95 sera approximativement : hpm = (1,2 + 0,95) × 5,50 = 11,825 m. De même la hauteur d'eau à basse mer sera hbm = (1,2 − 0,95) × 5,50 = 1,375 m.
Classement des composantes de la marée
| Nom | Cause | Période | Amplitude |
|---|---|---|---|
| Semi-diurnes | |||
| M2 | Principale lunaire | 12 h 25 min | 100 % |
| S2 | Principale solaire | 12 h 00 min | 46,5 % |
| N2 | Majeure lunaire elliptique | 12 h 40 min | 19,1 % |
| K2 | Déclinaison luni-solaire | 11 h 58 min | 12,6 % |
| Diurnes | |||
| O1 | Principale lunaire | 25 h 49 min | 41,5 % |
| K1 | Déclinaison luni-solaire | 23 h 56 min | 58,4 % |
| P1 | Principale solaire | 24 h 04 min | 19,3 % |
| Q1 | Majeure lunaire elliptique | 26 h 52 min | 7,9 % |
Niveau de la mer
D'une façon très simplifiée, le niveau de la mer est la ligne médiane entre une marée basse moyenne et une marée haute moyenne à un endroit côtier particulier, hors influence des vagues et des courants littoraux.
Lieux de marées remarquables
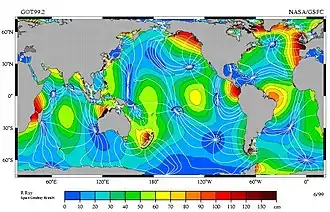
.jpg.webp)
.jpg.webp)
- Au Canada : dans la baie d'Ungava, le marnage peut atteindre 17[32] voire 20 mètres[33] et dans la baie de Fundy, 18,5 m. Ces baies sont les deux endroits où les marées les plus importantes au monde ont lieu et, selon les sources, on attribue à l'une ou à l'autre le record de marnage. Viennent ensuite Puerto Gallegos en Argentine (16,8 m), l'estuaire de la Severn en Angleterre (16,5 m), la baie de Frobisher au Canada (16,3 m), la baie du Mont-Saint-Michel en France (15 m)[34] et la baie de Saint-Brieuc en France (13 m).
- En Grande-Bretagne : le Canal de Bristol, avec 15 m de marnage.
- En France : jusqu'à 15 m de marnage dans la baie du Mont-Saint-Michel en Normandie, où il est traditionnellement dit que « la mer monte à la vitesse d'un cheval au galop » et entoure alors le Mont-Saint-Michel. Il est possible d'observer cet important marnage à Granville et plus largement le niveau de la mer pour ce site, entre autres, à partir du site des réseaux de référence des observations marégraphiques REFMAR[35].
- En Norvège : le Saltstraumen, remplissant un fjord de 400 millions de mètres cubes.
- En Australie-Occidentale : les Horizontal Falls, dans la région du Kimberley, avec 10 m de marnage environ.
- À Pondichéry (Inde) et dans certains ports du Viêt Nam, où il n'y a qu'une seule marée par jour.
Les modèles de marées
Caractéristique de l'onde de marée
L'attraction de la Lune et du Soleil crée une onde de marée qui, en se propageant, crée le phénomène de marée. La vitesse de propagation est élevée dans les eaux profondes (400 nœuds en Atlantique, soit environ 200 mètres par seconde), beaucoup plus faible dans les eaux peu profondes (30 nœuds en Manche, soit environ 15 mètres par seconde). Cette vitesse détermine le décalage des horaires de pleine mer en différents lieux.
De plus, la marée subit un retard par rapport aux situations astrales ; on parle d'âge de la marée. Sur les côtes françaises, elle vaut environ 36 h. À Brest, on verra donc les grandes marées 36 h après la pleine lune. Cette notion d'âge de la marée ne doit pas être confondue avec le temps de propagation de l'onde de marée décrite au paragraphe précédent.
L'ampleur et la périodicité de la marée dépendent du lieu : ils sont déterminés par de nombreux facteurs dont la taille du bassin maritime, sa profondeur, le profil des fonds marins, l'existence de bras de mer, la latitude, etc. Dans certaines mers, comme la Méditerranée, tous ces facteurs sont à l'origine d'une marée tellement faible qu'elle peut être négligée. Ailleurs les marées peuvent atteindre 15 m de marnage.
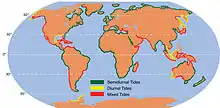
Selon la latitude du lieu et la morphologie de sa côte (caractéristiques ci-avant), on distingue des marées de quatre types[29] :
- régime de marée semi-diurne : deux pleines mers et deux basses mers ont lieu chaque jour lunaire (24 h 50 min), cas typique des côtes atlantiques européennes avec des amplitudes similaires ;
- régime de marée semi-diurne à inégalité diurne : régime similaire au précédent mais les hauteurs des pleines mers et des basses mers consécutives ont des amplitudes différentes (océan Indien) ;
- régime de marée diurne : régime plutôt rare dans lequel on observe une pleine mer et une basse mer par jour (golfes du Mexique, de Finlande, mer Baltique, mers d'Indochine) ;
- régime marée mixte : au cours de la lunaison, succession de marées marquant une transition progressive entre le type diurne et le type à inégalité diurne (côtes de l'océan Pacifique, mer Égée, mer Adriatique).
La marée en France métropolitaine
Elle est du type « semi-diurne », avec une période moyenne de 12 heures 25 minutes. Il y a donc un décalage chaque jour des heures de basse et pleine mer.
Le marnage est très variable. Celui-ci peut atteindre 14 mètres dans la baie du mont Saint-Michel lors des grandes marées, et être seulement quelques dizaines de centimètres en Méditerranée en mortes-eaux.
Dans la culture populaire
À Niue, la légende veut que le pluvier fauve chante à marée haute puis à nouveau à marée basse pour informer le pêcheur du changement de marée[36].
Notes et références
- Pourquoi y a-t-il alternance des vives et des mortes-eaux ?.
- Pêches et Océans Canada, « Les marées et courants de marée », gouvernement du Canada.
- La marée.
- Gilles Roulet, « La Marée », cours Ifremer (France) de master 2011-2012 [PDF].
- « Astrophysique ».
- Christian Le Provost. Contribution à l'étude des marées dans les mers littorales : Application à la Manche. Univ. Sci. et Médicale de Grenoble et Inst. Nat. Polytech., Grenoble, 1973.
- (en) G. H. Darwin, « On the precession of a viscous spheroid, and on the remote history of the Earth. », Philosophical Transactions of the Royal Society of London, vol. 170, , p. 447-538.
- (en) W. M. Kaula, « Tidal dissipation by solid friction and the resulting orbital evolution. », Reviews of Geophysics, vol. 2, , p. 661-684
- P. Melchior et B. Ducarme, « L’étude des phénomènes de marée gravimétrique. », Géodynamique, vol. 4 (1), , p. 3-14 (lire en ligne).
- Comment les marées solides et la gravimétrie influent sur la sismicité.
- Thérèse Encrenaz, Maria-Antonietta Barucci, Jean-Pierre Bibring. Le système solaire. Collection Savoirs Actuels, EDP Sciences, 2012 (ISBN 9782759802951).
- Encyclopædia Universalis, volume 14 Encyclopædia Universalis, 1990, p/522.
- SHOM, France.
- Jean-François Cliche, « Les grandes marées », le Soleil, .
- Synthèse d'une étude IRD (France) (N. Gratiot, E. J. Anthony, A. Gardel, C. Gaucherel, C. Proisy, J. T. Wells, Significant contribution of the 18.6 year tidal cycle to regional coastal changes, Nature Geoscience, volume 1, mars 2008 Doi : 10.1038/ngeo127, Letter), Université de Dunkerque. (Univers-Nature).
- K. Z. Kartvelichvili, « Étude des marées terrestres en tant que mécanisme de détente des tremblements de Terre », Marées terrestres, vol. 112, , p. 8216-8219.
- Hugues Journès, Yvon Georgelin, Jean-Marie Gassend, Pythéas, les Éditions de la Nerthe (2000), p. 69-70.
- René Taton, La Science antique et médiévale, Quadrige/PUF (1994), p. 319, 381-382.
- « La cause de ce phénomène, qui offre beaucoup de variétés, est dans le Soleil et dans la Lune. La mer, entre deux levers de lune, monte et redescend deux fois, toujours en vingt-quatre heures. À mesure que le ciel s'élève avec la Lune, les flots se gonflent ; puis ils reviennent sur eux-mêmes lorsque, après son passage au méridien, elle descend vers le couchant ; derechef, quand elle passe dans les parties inférieurs du ciel et gagne le méridien opposé, l'inondation recommence, et enfin le flot se retire jusqu'au lever suivant. La marée ne se fait jamais au même temps que le jour précédent, comme si elle était l'esclave de cet astre avide qui attire à lui les mers, et qui, chaque jour, se lève à un autre endroit que la veille. Le flux et le reflux alternent à des intervalles toujours égaux, qui sont de six heures chacun, non pas des heures d'un jour, d'une nuit ou d'un lieu quelconque, mais des heures équinoxiales. Aussi ces intervalles, évalués en heures vulgaires, paraissent-ils inégaux suivant le rapport des heures équinoxiales avec les heures vulgaires du jour et de la nuit ; ils ne sont égaux partout qu'aux équinoxes » L'Histoire naturelle L. 2 99..
- Pierre Duhem, Le système du Monde, L’astronomie latine au Moyen Âge, chap. II, 2, Hermann, 1958, p. 13.
- René Taton, La Science antique et médiévale, Quadrige/PUF (1994), p. 584
- Pierre Duhem, Le système du Monde, L’astronomie latine au Moyen Âge, chap. II, 2, Hermann, 1958, p. 20.
- « Introduction à l'astronomie, contenant les huit livres divisés d'Abu Ma'shar Abalachus », sur World Digital Library, (consulté le ).
- Pierre Duhem, La théorie physique. Vrin 2007, p. 324.
- Pierre Duhem, La théorie physique. Vrin 2007, p. 332.
- « La Lune attire les eaux de mer par une action magnétique » cité par Pierre Duhem, La théorie physique. Vrin 2007, p. 326.
- « Mais de tous les grands hommes qui ont philosophé sur cet effet si étonnant de la nature, c’est Kepler qui m’étonne le plus : cet esprit libre et pénétrant avait à sa disposition les mouvements attribués à la Terre, il a pourtant prêté l’oreille et donné son assentiment à un empire de la Lune sur l’eau, des propriétés occultes et autres enfantillages du même genre. » Dialogue sur les deux grands systèmes du monde, Seuil, 1992, p. 652.
- « L’explication était insoutenable car elle voulait que l’intervalle de deux marées hautes fût égal à la moitié d’un jour sidéral, tandis que les observations les plus obvies montrent qu’il est égal à une demi-journée lunaire. » Pierre Duhem, La théorie physique. Vrin 2007, p. 330.
- Isabelle Cojan, Maurice Renard, Sédimentologie, Dunod, (lire en ligne), p. 134.
- Magdeleine Moureau, Gerald Brace, Dictionnaire des Sciences de la Terre, Éditions Technip, , p. 517.
- Bulletin d'information de l'Institut géographique national de France no 73.
- Projet de parc national de la Baie-aux-Feuilles
- Portrait régional du Nord-du-Québec - Régions hydrographiques.
- Chantal Bonnot-Courtois, Bruno Caline, Alain L'Homer, Monique Le Vot, La Baie du Mont-Saint-Michel et l’estuaire de la Rance - Environnements sédimentaires, aménagements et évolution récente, Elf Exploration (Éditions), , p. 12.
- Réseaux de référence des observations marégraphiques (REFMAR).
- (en) Office de Tourisme, « Fishing », sur niueisland.com, (consulté le )
Voir aussi
Bibliographie
- Odile Guérin, Tout savoir sur les marées, Éditions Ouest-France, 2004, (ISBN 2-7373-3505-1)
- Bernard Simon, La marée océanique côtière, une coédition de l'institut océanographique et du SHOM, France, 2007, 433 pages, (ISBN 978-2-903581-32-9), ISSN 1272-0763, réf 942MOG, télécharger
- Les guides du SHOM (France), La Marée, 1997, réf OG941





























![+\cos ^{{2}}\phi _{{Lune}}\cos ^{{2}}\phi _{{P}}\cos 2(\lambda _{{P}}-\lambda _{{Lune}}){\Big ]}](https://img.franco.wiki/i/2b1f516e020f16462d5912af8ca06f69004451cf.svg)







