Accélération angulaire
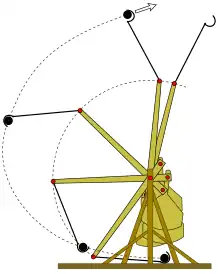
En physique, l'accélération angulaire est la variation de la vitesse angulaire au cours du temps. En unités dérivées du Système international, l'accélération angulaire s'exprime en radians par seconde carrée (rad/s2).
| Unités SI | rad⋅s−2 |
|---|---|
| Dimension | T −2 |
| Nature | Grandeur vectorielle intensive |
| Symbole usuel | α, , , |
| Lien à d'autres grandeurs | = |
| Conjuguée | Moment d'inertie |

L'accélération angulaire est une grandeur physique fondamentale pour caractériser le mouvement de rotation.
Énoncé
L'accélération est la première dérivée par rapport au temps (dérivée temporelle) de la vitesse angulaire, et la seconde dérivée temporelle de la position angulaire.
Si est la vitesse angulaire et la position angulaire, l'accélération angulaire est :
L'accélération angulaire est pour le mouvement de rotation l'homologue de l'accélération pour le mouvement de translation.
Accélérations tangentielle et centripète
L'accélération angulaire d'un corps est liée à ses accélérations tangentielle et centripète. Pour déterminer l'accélération tangentielle d'un corps, il suffit de multiplier son accélération angulaire par la mesure du rayon du cercle qui forme sa trajectoire[1].
Principe fondamental de la dynamique
L'accélération angulaire est l'une des variables de la deuxième loi de Newton appliquée en dynamique de rotation.
Ainsi, on peut déterminer le total des moments de forces () qui sont appliqués sur un corps à l'aide de l'accélération angulaire () de celui-ci et de son moment d'inertie (I). La sommation de tous les moments de force est équivalente au produit du moment d'inertie du corps par son accélération angulaire lorsque le corps est rigide et que la rotation s'effectue autour d'un axe de rotation fixe[2].
À-coup angulaire
L'à-coup angulaire est la dérivée par rapport au temps de l'accélération angulaire :
- .
Exemples
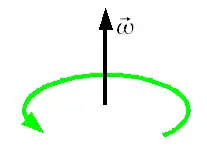
Roue en rotation autour d'un axe fixe
Posons une roue tournant dans le sens positif d'un référentiel donné. On dira que la vitesse et l'accélération angulaire sont parallèles lorsque la vitesse augmente puisqu'elles seront toutes deux positives. À l'inverse, elles seront anti-parallèles si la vitesse diminue car celle-ci restera positive alors que l'accélération angulaire deviendra négative[3].
Notes et références
- Benson 2009, p. 326
- Benson 2009, p. 337 - 340 (Expression valable lorsque l'axe de rotation est l'un des axes principaux d'inertie du corps considéré.)
- Kane et Sternheim 1986, p. 95
Annexes
Articles connexes
Bibliographie
![]() : document utilisé comme source pour la rédaction de cet article.
: document utilisé comme source pour la rédaction de cet article.
 Harris Benson (trad. Marc Séguin, Benoît Villeneuve, Bernard Marcheterre et Richard Gagnon), Physique 1 Mécanique, Édition du Renouveau Pédagogique, , 4e éd., 465 p.
Harris Benson (trad. Marc Séguin, Benoît Villeneuve, Bernard Marcheterre et Richard Gagnon), Physique 1 Mécanique, Édition du Renouveau Pédagogique, , 4e éd., 465 p. Joseph W. Kane et Morton M. Sternheim (adaptation Michel Delmelle), Physique, Interédition, , 775 p.
Joseph W. Kane et Morton M. Sternheim (adaptation Michel Delmelle), Physique, Interédition, , 775 p.











