Polarisation circulaire
La polarisation circulaire d'un rayonnement électromagnétique est une polarisation où la norme du vecteur du champ électrique ne change pas alors que son orientation change selon un mouvement de rotation.
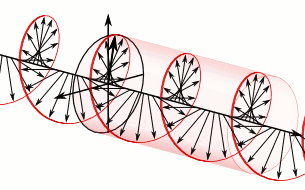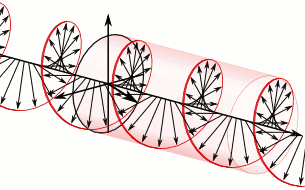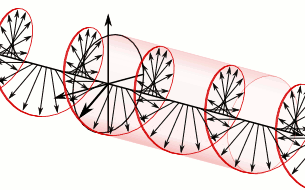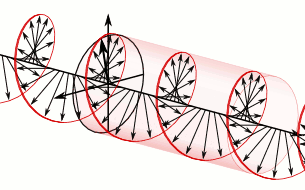
En électrodynamique la norme et la direction d'un champ électrique sont représentés par un vecteur comme on peut le voir dans l'animation ci-contre. Dans le cas d'une onde polarisée circulairement, les vecteurs d'un champ électrique, à un point donné dans l'espace, décrivent un cercle en fonction du temps. Si l'on observe l'onde à un moment donné, le vecteur du champ électrique de l'onde décrit un mouvement hélicoïdal le long de la direction de propagation.
La polarisation circulaire est un cas particulier de la polarisation elliptique (en), tout comme la polarisation linéaire (en).
Le phénomène de polarisation se présente comme une conséquence du fait que la lumière se comporte comme une onde transversale à deux dimensions.
Convention du sens horaire/anti-horaire
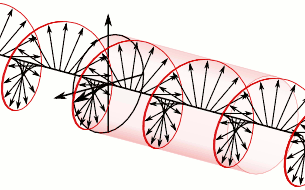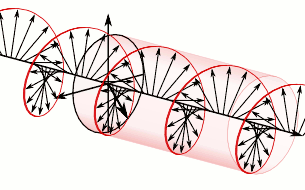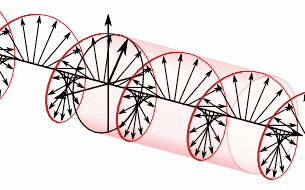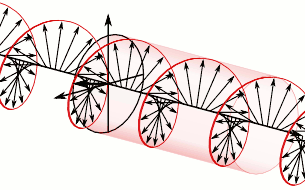

La polarisation circulaire peut être définie dans le sens horaire ou anti-horaire, selon la direction dans laquelle le vecteur champ électrique tourne. Deux conventions historiques opposées existent.
Du point de vue de la source
Avec cette convention, la polarisation est définie du point de vue de la source. Lors de l'utilisation de cette convention, le sens horaire ou anti-horaire est déterminé en pointant le pouce droit ou gauche à l'opposé de la source, dans la même direction que la propagation de l'onde. Si ce sont les doigts de la main droite qui tournent dans le même sens que le champ, alors la polarisation est horaire, tandis qu'elle est anti-horaire si ce sont les doigts de la main gauche qui pointent dans la même direction que le champ.
Avec cette convention, le vecteur champ électrique onde polarisée circulairement est défini comme suit :
Comme exemple spécifique, reportez-vous à l'onde polarisée circulairement dans la première animation. Grâce à cette convention où l'onde est définie comme étant dans le sens horaire parce que quand on pointe son pouce de la main droite dans la même direction de propagation de l'onde, les doigts de la main pointent dans le même sens de rotation du champ dans le temps (règle de la main droite). Il est considéré comme étant une polarisation circulaire dans le sens horaire en fonction du point de vue de la source, en regardant dans la même direction de propagation de l'onde, le champ tourne dans le sens horaire. La seconde animation est celle de la lumière dans le sens anti-horaire avec cette même convention.
Cette convention est conforme aux standards de l'Institute of Electrical and Electronics Engineers (IEEE) et, par conséquent, elle est généralement utilisée dans la communauté des ingénieurs[1] - [2] - [3]
Les physiciens quantiques utilisent également cette convention de sens car elle est conforme à leur convention de sens pour le spin d'une particule[4].
Les radioastronomes utilisent aussi cette convention conformément à la résolution adoptée en 1973 par l'Union astronomique internationale[5].
Du point de vue du receveur
Dans cette convention alternative, la polarisation est définie du point de vue du récepteur et est exactement l'inverse de la première. Ainsi, le sens horaire ou anti-horaire est déterminé en pointant respectivement le pouce de la main gauche ou droite vers la source, à l'opposé de la direction de propagation, puis la direction où les autres doigts de la main pointe indique le sens de rotation du vecteur champ électrique dans le temps.
Lorsque cette convention est utilisée, contrairement à l'autre convention, le sens de l'onde correspond au sens de la nature de type « tire bouchon » du champ dans l'espace. Plus précisément, si l'on observe une onde de sens horaire à un point donné dans le temps, quand on courbe les doigts de sa main droite autour de l'hélice, le pouce pointe dans la direction dans laquelle l'hélice progresse donnant ce sens de rotation.
Beaucoup de manuels d'optique utilisent cette seconde convention[6] - [7] ainsi que l'Union internationale de chimie pure et appliquée (UICPA)[8].
Utilisation des deux conventions
Comme indiqué précédemment, il y a beaucoup de confusion en ce qui concerne ces deux conventions. En règle générale, l'ingénierie, la physique quantique, la radio et les communautés astronomiques utilisent la première convention, où l'onde est observée du point de vue de la source[2] - [4] - [5], alors que dans de nombreux manuels de physique optique, la seconde convention est utilisée, donc la lumière est observée à partir du point de vue du récepteur[4] - [6].
Pour éviter toute confusion, il est utile de préciser «tel que vue du point de vue de la source» ou «tel que défini à partir du point de vue du récepteur» lors de l'examen des questions de polarisation.
Description générale


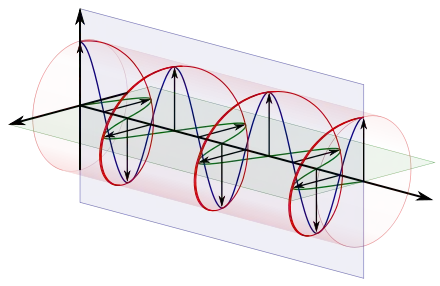
À droite se trouve une illustration des vecteurs champ électrique d’une onde électromagnétique polarisée circulairement. Le champ électrique de ces vecteurs a une norme constante, mais sa direction change selon un mouvement de rotation. Étant donné qu'ils forment une onde plane, chaque vecteur représente la norme et la direction du champ électrique pour un plan entier qui est perpendiculaire à l’axe. deux images dans l’article sur les onde plane pour mieux illustrer le concept.
Cette lumière est considérée comme étant polarisée circulairement vers la droite. C'est-à-dire, dans le sens horaire vu du récepteur. Étant donné que c'est une onde électromagnétique, chaque vecteur champ électrique possède un vecteur champ magnétique correspondant, mais non illustré. Celui-ci est à angle droit avec le vecteur champ électrique et est proportionnel à sa norme. En conséquence, le vecteur champ magnétique se trace une seconde hélice s'il est exposé.
La polarisation circulaire est souvent utilisée dans le domaine de l'optique. Dans cette section, l'onde électromagnétique sera simplement appelée lumière.
La nature de la polarisation circulaire, et sa relation avec les autres sortes de polarisations, est souvent comprise comme étant le champ électrique qui se divise en deux composantes qui sont à angle droit l'un par rapport à l'autre (voir la seconde illustration à droite). La composante verticale et son plan correspondant sont illustrés en bleu alors que la composante horizontale et son plan sont illustrés en vert.
La composante horizontale de la droite (par rapport à sa direction de propagation) devance la composante verticale par un quart de longueur d'onde. C'est cette relation de phase en quadrature qui crée l'hélice et amène les points d'amplitude maximales de la composante verticale en correspondance avec les points d'amplitude zéro de la composante horizontale, et vice versa. Le résultat de cet alignement est qu'il existe des vecteurs de sélection, correspondants à l'hélice, ce qui concorde exactement au maximum des composantes horizontales et verticales. (Pour minimiser l'encombrement visuel, seuls les vecteurs d'hélice sont affichés.)
Pour illustrer comment ce déphasage en quadrature correspond à un champ électrique qui tourne tout en maintenant une ampleur constante, imaginez un point qui voyage dans le sens horaire sur un cercle. Examinez comment les déplacements verticaux et horizontaux du point, par rapport au centre du cercle, varient de façon sinusoïdale dans le temps et sont déphasés par quart d'un cycle. Les déplacements sont censés être en opposition de phase par un quart d'un cycle, car le déplacement horizontal maximum (vers la gauche) atteint un quart de cycle avant que le déplacement vertical maximum l'atteigne. Maintenant, en se référant à nouveau à l'illustration, imaginez que le centre du cercle qui vient d'être décrit se déplace le long de l'axe de l'avant vers l'arrière. Le point encerclant va tracer une hélice avec le déplacement vers la gauche de notre vision, entraînant le déplacement vertical. De même que les déplacements horizontaux et verticaux du point de rotation sont déphasées d'un quart d'un cycle dans le temps, l'amplitude des composantes horizontale et verticale du champ électrique sont déphasées d'un quart de longueur d'onde.

La paire d'illustrations suivante, est celle de la lumière polarisée circulairement dans le sens anti-horaire lorsqu'elle est vue par le récepteur. Puisque c'est dans le sens anti-horaire, la droite (par rapport à la direction de diffusion) de la composante horizontale se situe maintenant derrière la composante verticale par un quart d'une longueur d'onde plutôt que de la diriger.
Inversion du sens par déphasage
Pour convertir une direction donnée de la lumière polarisée à l'autre direction on peut utiliser une lame demi-onde. Une lame demi-onde déphase une composante donnée de la lumière d'une demi longueur d'onde par rapport à la composante à laquelle elle est orthogonale.
Inversion du sens par réflexion
Le sens de la lumière polarisée est également inversé quand elle est réfléchie par une surface avec une incidence normale. Au moment de cette réflexion, la rotation du plan de polarisation de la lumière réfléchie est identique à celle du champ incident. Cependant, avec la propagation dans la direction opposée, le même sens de rotation qui serait décrit comme « horaire » pour le faisceau incident est « anti-horaire » pour la propagation dans le sens inverse, et vice versa. Mis à part l'inversion du sens de rotation, l'ellipticité de la polarisation est également préservée (sauf dans le cas d'une réflexion par une surface biréfringente).
Notez que ce principe ne fonctionne strictement que pour la lumière réfléchie avec une incidence normale. Par exemple, la lumière polarisée circulairement dans le sens horaire réfléchie par une surface diélectrique en incidence rasante (un angle au-delà de l'angle de Brewster) émergera encore comme étant dans le sens horaire, mais polarisée elliptiquement. La lumière réfléchie par un métal à incidence non normale verra généralement son ellipticité changée ainsi. De telles situations peuvent être résolues par la décomposition de la polarisation circulaire incidente (ou autre) en composantes de polarisation linéaire parallèle et perpendiculaire au plan d'incidence, communément nommé respectivement p et s. Les composantes reflétées dans les polarisation linéaire p et s se trouvent en appliquant les coefficients de Fresnel de réflexion, qui sont généralement différents pour ces deux polarisations linéaires. Seulement dans le cas particulier de l'incidence normale, où il n'y a pas de distinction entre s et p, les coefficients de Fresnel sont identiques pour les deux composantes, menant à la propriété ci-dessus.

Conversion à partir de la polarisation linéaire
La lumière polarisée linéairement peut être convertie en lumière polarisée circulairement en la faisant passer à travers une lame à retard d'un quart d'onde avec ses axes à 45° par rapport à son axe de polarisation. En fait, c'est la manière la plus courante de produire la polarisation circulaire en pratique. Notez que faire passer de la lumière polarisée linéairement dans cette lame produira généralement de la polarisation elliptique.
Radio FM
Le terme « polarisation circulaire » est souvent utilisé à tort pour décrire les signaux de polarité mixtes utilisés principalement dans la radio FM (87,5 à 108,0 MHz aux États-Unis), où des composantes verticale et horizontale se propagent simultanément seules ou dans un ensemble combiné. Cela a pour effet de produire une meilleure pénétration dans les bâtiments et les zones de réception difficile qu'un signal avec un seul plan de polarisation.
Ce serait un cas où il serait plus approprié d'appeler la polarisation : polarisation aléatoire parce que la polarisation à un récepteur, bien que constante, varie en fonction de la direction de l'émetteur et d'autres facteurs dans la conception de l'antenne émettrice. Voir les paramètres de Stokes.
Le terme « radio FM » ci-dessus, réfère à un radio diffuseur, et non à un radio émetteur-récepteur, qui utilise presque exclusivement la polarisation verticale.
Dichroïsme circulaire
Le dichroïsme circulaire (DC) est l'absorption différentielle de la lumière polarisée circulairement dans le sens horaire et anti-horaire. Le dichroïsme circulaire est la base d'une forme de spectroscopie qui peut être utilisée pour déterminer l'isomérie optique de la structure secondaire des molécules.
En général, ce phénomène sera exposé dans les bandes d'absorption de toute molécule optiquement active. Par conséquent, on rencontre le dichroïsme circulaire dans la plupart des molécules biologiques car elles contiennent des molécules dextrogyres, tels certains sucres, et lévogyres, tels certains acides aminés.
Il est à noter qu'une structure secondaire conférera aussi un dichroïsme circulaire à ses molécules respectives. Par conséquent, l'hélice alpha, le feuillet bêta, la pelote aléatoire de la protéine ainsi que la double-hélice des acides nucléiques ont des signatures de spectres de dichroïsme circulaire représentatives de leurs structures.
De plus, sous les bonnes conditions, même les molécules non-chirales vont exposer un dichroïsme circulaire magnétique (en) qui sera induit par un champ magnétique.
Luminescence circulairement polarisée
La luminescence circulairement polarisée (LCP) peut se produire lorsqu'un luminophore ou un ensemble de luminophores est chiral. La mesure dans laquelle les émissions sont polarisées est quantifiée de la même manière que pour le dichroïsme circulaire, en termes de facteur de « dissymétrie »[9], aussi parfois appelé le « facteur d'anisotropie ».
Cette valeur est donnée par
où correspond au rendement quantique de la lumière polarisée circulairement vers la gauche, et à celui de la lumière polarisée vers la droite.
La valeur absolue maximale de , correspondant à la polarisation circulaire purement horaire ou anti-horaire, est donc 2. Pendant ce temps, la plus petite valeur absolue que peut atteindre, correspondant à la lumière polarisée linéairement ou non polarisée, est zéro.
Description mathématique
La solution classique d'onde plane sinusoïdale de l'équation d'onde électromagnétique pour les champs électriques et magnétiques est :
où
- est le nombre d'onde,
- est la vitesse angulaire de l'onde,
- est une matrice orthogonale dont les colonnes s'étendent et traversent le plan x-y,
- est la vitesse de la lumière,
- est l'amplitude du champ et
- est le vecteur de Jones dans le plan x-y.
Si est en rotation de radian par rapport à et que l'amplitude x est égale à l'amplitude y, l'onde est polarisée circulairement. Le vecteur de Jones devient donc :
où le signe plus indique une polarisation circulaire à gauche et le signe moins indique une polarisation circulaire à droite.
Dans le cas d'une polarisation circulaire, le vecteur du champ électrique d'une amplitude constante tourne dans le plan x-y.
Si les vecteurs de base sont définis de telle sorte que :
et
alors l'état de la polarisation peut être écrite dans la « base R-L » comme :
où :
et
Antennes
Un bon nombre de différents types d'éléments d'antenne peut être utilisé pour produire un rayonnement polarisé circulairement (ou presque). Selon Balanis[10], on peut utiliser des éléments dipolaires:
« deux dipôles croisés fournissent les deux composantes du champ orthogonale[...] Si les deux dipôles sont identiques, l'intensité du champ le long de chaque zénith [...] serait de la même intensité. De plus, si les deux dipôles sont alimentés avec un déphasage de 90° degrés, la polarisation le long des zéniths serait circulaire [...] Une façon d'obtenir un déphasage de 90° entre les deux composantes orthogonales, rayonnée respectivement par les deux dipôles, est en alimentant l'une des deux dipôles avec une ligne de transmission d'un quart d'onde qui est plus longue ou plus courte que celle de l'autre[trad 1]. »
— Constantine Balanis, Antenna Theory - Analysis and Design[11]
ou éléments hélicoïdaux :
« Pour atteindre une polarisation circulaire [en mode axial] [...] la circonférence C de l'hélice doit être [...] de C / longueur d'onde = 1 presque optimale, et l'espacement des S = longueur d'onde / 4[trad 2]. »
— Constantine Balanis, Antenna Theory - Analysis and Design[12]
ou éléments planaires ou patch :
« [...] la polarisation circulaire et elliptique peut être obtenue en utilisant divers arrangements d'alimentation ou de légères modifications apportées aux éléments [...] Polarisation circulaire peut être obtenue si deux modes orthogonaux sont excités avec une déphasage de 90° entre eux. Ceci peut être accompli en ajustant les dimensions physiques du patch [...] Pour un élément planaire carré, la meilleure façon d'exciter la polarisation circulaire est d'alimenter l'élément aux deux bords adjacents [...] le déphasage est obtenue en alimentant l'élément avec un diviseur de puissance à 90°[trad 3]. »
— Constantine Balanis, Antenna Theory - Analysis and Design[13]
Mécanique quantique
Selon la mécanique quantique, la lumière est composée de photons. La polarisation est une manifestation du moment angulaire intrinsèque (le spin) du photon. Plus précisément, dans la mécanique quantique, la direction de rotation d'un photon est lié à la chiralité de la lumière circulairement polarisée et la rotation d'un faisceau de photons est similaire à la rotation d'un faisceau de particules, tel que les électrons[14].
Dans la nature

Seuls quelques mécanismes dans la nature sont connus pour produire systématiquement de la lumière polarisée circulairement. En 1911, Albert Abraham Michelson a découvert que la lumière réfléchie par la cétoine dorée Chrysina resplendens est partiellement polarisée dans le sens anti-horaire. Depuis lors, la polarisation circulaire a été observée chez plusieurs autres scarabées comme le Chrysina gloriosa[15], ainsi que certains crustacés comme la crevette-mante. Dans ces cas, la chitine de ces animaux est de forme hélicoïdale au niveau moléculaire[16].
La bioluminescence des larves de lucioles est également polarisée circulairement, tel que rapporté en 1980 pour les espèces lucicrescens Photuris (nl) et Photuris versicolor (nl). Pour les lucioles, il est plus difficile de trouver une explication au microscope pour la polarisation, car les lanternes gauche et droite de larves se sont avérées émettre une lumière polarisée de sens opposé. Les auteurs suggèrent que la lumière commence avec une polarisation linéaire en raison des inhomogénéités à l'intérieur des photocytes alignés, et cela se transforme en polarisation circulaire en passant à travers le tissu linéairement biréfringent[17].
Les interfaces eau et air constituent une autre source de polarisation circulaire. La lumière du Soleil qui est dispersée remonte vers la surface et est polarisée linéairement. Si cette lumière est alors réfléchie de manière totale interne vers le bas, sa composante verticale subit un décalage de phase. Pour un observateur regardant sous l'eau, la faible lumière en dehors de la fenêtre de Snell est donc (partiellement) polarisée circulairement[18].
Deux espèces de crevettes-mantes se sont avérées être capables de détecter la lumière polarisée[19] - [20].
Astronomie
La lumière des étoiles devient partiellement polarisée linéairement par la diffusion causée par des grains de poussière interstellaire allongés dont les axes longs ont tendance à être orientés perpendiculairement au champ magnétique galactique. Selon le mécanisme de Davis-Greenstein, les grains tournent rapidement autour de leur axe de rotation le long du champ magnétique. La lumière polarisée le long de la direction du champ magnétique perpendiculaire à la ligne de visée est transmise, alors que la lumière polarisée dans le plan défini par le grain en rotation est bloqué. Ainsi, la direction de polarisation peut être utilisée pour cartographier le champ magnétique galactique. Le degré de polarisation est de l'ordre de 1,5 % pour une étoile à 1 000 parsecs de distance[21].
Normalement, une fraction beaucoup plus faible de lumière polarisée circulairement se trouve dans la lumière des étoiles. Serkowski, Mathewson et Ford[22] ont mesuré la polarisation de 180 étoiles avec des filtres U, B, V, R et I. Ils ont observé une proportion maximale de polarisation circulaire de dans le filtre R.
L'explication est que le milieu interstellaire est mince d'un point de vue de l'optique. La lumière des étoiles qui voyage à travers une colonne d'un kiloparsec de long verra sa magnitude disparaître. La profondeur optique sera donc de ~1. Une profondeur optique de 1 correspond à un parcours sans obstacles moyen, qui est la distance moyenne parcourue par un photon avant qu'un grain de poussière ne le diffuse. Ainsi, en moyenne, un photon de lumière d'étoile est diffusé à partir d'un seul grain interstellaire, une diffusion multiple (qui produit une polarisation circulaire) est donc beaucoup moins présente. Selon des observations[21], la fraction d'une diffusion simple polarisée linéairement est de . La polarisation circulaire provenant d'une diffusion multiple se rapproche de , nous nous attendons donc à une fraction de lumière polarisée circulairement de.
La lumière provenant d'étoiles de type précoce ne fait que très peu de polarisation intrinsèque. Kemp et al.[23] ont mesuré la polarisation optique du Soleil avec une précision de . Ils ont obtenu une limite supérieure de pour (fraction de polarisation linéaire) et pour (fraction de polarisation circulaire).
Le milieu interstellaire peut produire de la lumière polarisée circulairement (PC) à partir de la lumière non polarisée par diffusion séquentielle à partir de grains de poussière interstellaires allongés et alignés dans des directions différentes. Une possibilité est que l'alignement des grains le long de la ligne de visée se tordent due à la variation du champ magnétique galactique. Une autre serait que la ligne de visée passe par plusieurs nuages. Pour ces mécanismes, la fraction maximale de PC prévue est , où est la fraction de lumière polarisée linéairement (PL). Kemp & Wolstencroft[24] ont trouvé de la PC dans six étoiles de type précoce (aucune polarisation intrinsèque) qu'ils étaient en mesure d'attribuer au premier mécanisme mentionné ci-dessus. Dans tous les cas, en lumière bleue.
Martin[25] a démontré que le milieu interstellaire peut convertir la lumière PL en lumière PC par diffusion à partir de grains de poussière interstellaires partiellement alignées ayant un indice de réfraction complexe. Cet effet a été observé dans le cas de la lumière émise par la Nébuleuse du Crabe par Martin, Illing et Angel[26].
Un environnement circumstellaire (en) optiquement épais peut potentiellement produire une PC beaucoup plus grande que dans le milieu interstellaire. Martin [25] a suggéré que la lumière PL peut devenir PC près d'une étoile par diffusion multiple dans un nuage de poussière épais optiquement, circumstellaire et asymétrique. Ce mécanisme a été invoqué par Bastien, Robert et Nadeau[27] pour expliquer la PC mesurée à 768 nm dans l'étoile 6 T-Tauri. Ils ont trouvé une PC maximale de . Quant à lui, Serkowski[28] a mesuré un PC de pour la super-géante rouge NML Cygni. Chrysostomou et al.[29] ont trouvé une PC avec un allant jusqu'à 0,17 dans la région de formation d'étoiles OMC-1 d'Orion, et l'ont expliqué par la réflexion de la lumière des étoiles à partir de grains aplatis et alignés dans la nébuleuse de poussière.
La polarisation circulaire de la lumière du zodiaque et de la lumière diffuse galactique de la Voie lactée a été mesurée à la longueur d'onde de 550 nm par Wolstencroft et Kemp[30]. Ils ont trouvé une valeur de , laquelle est supérieure à celle des étoiles ordinaires, sans doute en raison de la diffusion multiple à partir de grains de poussière.
Notes et références
Notes
- (en) « two crossed dipoles provide the two orthogonal field components... If the two dipoles are identical, the field intensity of each along zenith ... would be of the same intensity. Also, if the two dipoles were fed with a 90° degree time-phase difference (phase quadrature), the polarization along zenith would be circular... One way to obtain the 90° time-phase difference between the two orthogonal field components, radiated respectively by the two dipoles, is by feeding one of the two dipoles with a transmission line which is 1/4 wavelength longer or shorter than that of the other. »
- (en) « To achieve circular polarization [in axial or end-fire mode] ... the circumference C of the helix must be ... with C/wavelength = 1 near optimum, and the spacing about S = wavelength/4. »
- (en) « circular and elliptical polarizations can be obtained using various feed arrangements or slight modifications made to the elements... Circular polarization can be obtained if two orthogonal modes are excited with a 90° time-phase difference between them. This can be accomplished by adjusting the physical dimensions of the patch ... For a square patch element, the easiest way to excite ideally circular polarization is to feed the element at two adjacent edges ... The quadrature phase difference is obtained by feeding the element with a 90° power divider. »
Références
- (en) IEEE Std 149-1979 (R2008), «IEEE Standard Test Procedures for Antennas". Reaffirmed December 10, 2008, Approved December 15, 1977, IEEE-SA Standards Board. Approved October 9, 2003, American National Standards Institute. (ISBN 0-471-08032-2). DOI 10.1109/IEEESTD.1979.120310, sec. 11.1, p. 61."the sense of polarization, or handedness... is called right handed (left handed) if the direction of rotation is clockwise (anti-clockwise) for an observer looking in the direction of propagation»
- (en) Electromagnetic Waves & Antennas – S. J. Orfanidis: Footnote p. 45, «most engineering texts use the IEEE convention and most physics texts, the opposite convention.»
- (en) Electromagnetic Waves & Antennas – S. J. Orfanidis Pg 44 «Curl the fingers of your left and right hands into a fist and point both thumbs towards the direction of propagation»
- (en) Lectures on Physics Feynman (Vol. 1, ch.33-1) «If the end of the electric vector, when we look at it as the light comes straight toward us, goes around in an anti-clockwise direction, we call it right-hand circular polarization.... Our convention for labeling left-hand and right-hand circular polarization is consistent with that which is used today for all the other particles in physics which exhibit polarization (e.g., electrons). However, in some books on optics the opposite conventions are used, so one must be careful."
- (en) IAU General Assembly Meeting, 1973, Commission 40 (Radio Astronomy/Radioastronomie), 8. POLARIZATION DEFINITIONS -- «A working Group chaired by Westerhout was convened to discuss the definition of polarization brightness temperatures used in the description of polarized extended objects and the galactic background. The following resolution was adopted by Commissions 25 and 40: 'RESOLVED, that the frame of reference for the Stokes parameters is that of Right Ascension and Declination with the position angle of electric-vector maximum, q, starting from North and increasing through East. Elliptical polarization is defined in conformity with the definitions of the Institute of Electrical and Electronics Engineers (IEEE Standard 211, 1969). This means that the polarization of incoming radiation, for which the position angle, q, of the electric vector, measured at a fixed point in space, increases with time, is described as right-handed and positive.'"
- (en)Polarization in Spectral Lines. 2004 E. Landi Degl’innocenti, M Landolfi Section 1.2 «When... the tip of the electric field vector rotates clockwise for an observer facing the radiation source... (it will be considered)... positive (or righthanded) circular polarization, Our convention... agrees with those proposed in the classical textbooks on polarized light by Shurcliff (1952) and by Clarke and Grainger (1971). The same convention is also used, although with some few exceptions, by optical astronomers working in the field of polarimetry. Many radio astronomers, on the other hand, use the opposite convention.
- (en)HANDBOOK OPTICS Volume I, Devices, Measurements and Properties, Michael Bass Page 272 Footnote: «Right-circularly polarized light is defined as a clockwise rotation of the electric vector when the observer is looking against the direction the wave is traveling."
- S. E. Braslavsky, « Glossary of terms used in photochemistry, 3rd edition (IUPAC Recommendations 2006) », Pure and Applied Chemistry, vol. 79, no 3, , p. 293-465 (DOI 10.1351/pac200779030293, lire en ligne)
- (en)
- Balanis 2005.
- Balanis 2005, p. 80.
- Balanis 2005, p. 571.
- Balanis 2005, p. 859.
- (en) David Park Sec, Introduction to Quantum Theory, 2e éd., chap. 2.2, p. 32 :
« the polarization of a beam of light is exactly the same kind of thing as the spin of a beam of electrons, the differences of terminology reflecting only the accidents of the historical order of discovery. »
- (en)Structural Origin of Circularly Polarized Iridescence in Jeweled Beetles.
- (en) Hegedüs, Ramón; Győző Szélb; and Gábor Horváth, « Imaging polarimetry of the circularly polarizing cuticle of scarab beetles (Coleoptera: Rutelidae, Cetoniidae) », Vision Research, vol. 46, no 17, , p. 2786–2797 (PMID 16564066, DOI 10.1016/j.visres.2006.02.007, lire en ligne)
- (en)Wynberg, Hans; Meijer, E.W.; Hummelen, J.C.; Dekkers, H.P.J.M.; Schippers, P.H.; Carlson, A.D, « Circular polarization observed in bioluminescence », Nature, vol. 286, no 5773, , p. 641–642 (DOI 10.1038/286641a0, Bibcode 1980Natur.286..641W, lire en ligne)
- (en) Horváth, Gábor and Dezsö Varjú, Polarized Light in Animal Vision : Polarization Patterns in Nature, Berlin/New York, Springer, , 100–103 p. (ISBN 3-540-40457-0)
- (en)Tsyr-Huei Chiou, Sonja Kleinlogel, Tom Cronin, Roy Caldwell, Birte Loeffler, Afsheen Siddiqi, Alan Goldizen & Justin Marshall, « Circular polarization vision in a stomatopod crustacean », Current Biology, vol. 18, no 6, , p. 429–34 (PMID 18356053, DOI 10.1016/j.cub.2008.02.066)
- Sonja Kleinlogel & Andrew White, « The secret world of shrimps: polarisation vision at its best », PLoS ONE, vol. 3, no 5, , e2190 (PMID 18478095, PMCID 2377063, DOI 10.1371/journal.pone.0002190, Bibcode 2008PLoSO...3.2190K, arXiv 0804.2162, lire en ligne)
- (en) Pablo Fosalba, Alex Lazarian, Simon Prunet et Jan A. Tauber, « Statistical Properties of Galactic Starlight Polarization », ApJ, vol. 564, no 2, , p. 722 (DOI 10.1086/324297, Bibcode 2002ApJ...564..762F, arXiv astro-ph/0105023)
- (en) K. Serkowski et Mathewson and Ford, « Wavelength dependence of interstellar polarization and ratio of total to selective extinction », ApJ, vol. 196, , p. 261 (DOI 10.1086/153410, Bibcode 1975ApJ...196..261S)
- (en) J. C. Kemp et al., « The optical polarization of the Sun measured at a sensitivity of parts in ten million », Nature, vol. 326, no 6110, , p. 270 (DOI 10.1038/326270a0, Bibcode 1987Natur.326..270K)
- (en) James C. Kemp et Wolstencroft, « Interstellar Circular Polarization: Data for Six Stars and the Wavelength Dependence », ApJ, vol. 176, , p. L115 (DOI 10.1086/181036, Bibcode 1972ApJ...176L.115K)
- Martin, « Interstellar circular polarization », MNRAS, vol. 159, , p. 179 (DOI 10.1093/mnras/159.2.179, Bibcode 1972MNRAS.159..179M)
- (en) Martin, Illing et Angel, « Discovery of interstellar circular polarization in the direction of the Crab nebula », MNRAS, vol. 159, , p. 191 (DOI 10.1093/mnras/159.2.191, Bibcode 1972MNRAS.159..191M)
- (en) Pierre Bastein et Robert and Nadeau, « Circular polarization in T Tauri stars. II - New observations and evidence for multiple scattering », ApJ, vol. 339, , p. 1089 (DOI 10.1086/167363, Bibcode 1989ApJ...339.1089B)
- (en) K. Serkowski, « Infrared Circular Polarization of NML Cygni and VY Canis Majoris », ApJ, vol. 179, , p. L101 (DOI 10.1086/181126, Bibcode 1973ApJ...179L.101S)
- (en) Antonio Chrysostomou et al., « Polarimetry of young stellar objects - III. Circular polarimetry of OMC-1 », MNRAS, vol. 312, , p. 103 (DOI 10.1046/j.1365-8711.2000.03126.x, Bibcode 2000MNRAS.312..103C)
- (en) Ramon D. Wolstencroft et Kemp, « Circular Polarization of the Nightsky Radiation », ApJ, vol. 177, , p. L137 (DOI 10.1086/181068, Bibcode 1972ApJ...177L.137W)
Bibliographie
![]() : document utilisé comme source pour la rédaction de cet article.
: document utilisé comme source pour la rédaction de cet article.
- (en) Constantine A. Balanis, Antenna Theory : Analysis and Design, John Wiley & Sons, , 3e éd., 1136 p. (présentation en ligne).

- (en) John D. Jackson, Classical Electrodynamics, New York, Wiley, (ISBN 0-471-30932-X)
- (en) M. Born et E. Wolf, Principles of optics : electromagnetic theory of propagation, interference and diffraction of light, Cambridge, Cambridge University Press, , 952 p. (ISBN 0-521-64222-1)
Voir aussi
Articles connexes
- polarisation (optique)
- Polariseur
- Projection en relief stéréoscopique
- Chiralité
- polarisation photonique (en)
- Lame à retard
Liens externes
- http://www.polarization.com/beetle/beetle.html
- Article on the mantis shrimp and circular polarization
- Animation of Circular Polarization (on YouTube)
- Comparison of Circular Polarization with Linear and Elliptical Polarizations (YouTube Animation)
- Reversal of handedness of circularly polarized light by mirror. A demonstration – simple, cheap & instructive





![{\mathbf {E}}({\mathbf {r}},t)=\mid {\mathbf {E}}\mid {\mathrm {Re}}\left\{{\mathbf {Q}}|\psi \rangle \exp \left[i\left(kz-\omega t\right)\right]\right\}](https://img.franco.wiki/i/71d37a5c3f005f63db9f395a3468a014e4d9c8ed.svg)



![{\mathbf {Q}}=\left[{\hat {{\mathbf {x}}}},{\hat {{\mathbf {y}}}}\right]](https://img.franco.wiki/i/1c6f209c9644cf3ab69fd75e6d696bb9278c0c12.svg)


























