Parsec
Le parsec (/paʁ.sεk/)[1], de symbole pc, est une unité de longueur utilisée en astronomie. Il est défini comme valant exactement 648 000π unités astronomiques, soit environ 3,26 années-lumière.
| Parsec | |
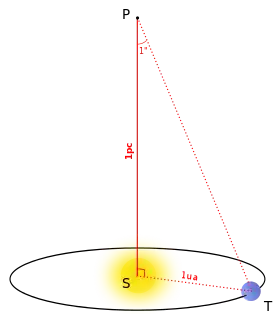 Ancienne définition du parsec (la représentation schématique n'est pas à l'échelle). | |
| Informations | |
|---|---|
| Unité de… | longueur |
| Symbole | pc |
Le nom parsec est la contraction de « parallaxe-seconde », une expression se rapportant à sa définition historique, désormais obsolète (cf. figure).
Terminologie
« Parsec »[1] - [2] - [3] est emprunté à l'anglais parsec[1], mot-valise[4] proposé par l'astronome britannique Herbert Hall Turner à partir de par[allax] (en français, « parallaxe ») et de sec[ond] (« seconde »)[1].
D'après Frédéric Arenou[4], le parsec a été utilisé pour la première fois en par l'astronome allemand Hermann Kobold, sous le nom de Sternweite (littéralement « distance stellaire » en allemand)[5]. En 1913, l'astronome britannique Frank Watson Dyson propose de nommer l'unité macron[6] et Turner astron[7]. Le terme de macron fut rejeté par Frank Watson Dyson, par crainte d'une confusion avec le terme micron[8].
En , la commission « Notations » de l'Union astronomique internationale suggère l'utilisation de l'année-lumière, « surtout dans les articles populaires », et du parsec, « ou de préférence une unité dix fois plus grande avec un nom distinct »[9].
Définition
Définition historique
Historiquement, le parsec est défini comme la distance à laquelle une unité astronomique (ua) sous-tend un angle d’une seconde d'arc. Autrement dit, la distance à partir de laquelle on verrait la distance Terre-Soleil, sous un angle d'une seconde d'arc. Cette définition est néanmoins légèrement ambiguë et n'avait par ailleurs jamais été officialisée, ce qui conduisait à des variations, certes faibles, mais inutilement présentes, de la valeur (en unités du Système international) adoptée pour cette unité. La définition du parsec a donc été précisée et à la même occasion officialisée en note de la résolution B2 adoptée lors de l'assemblée générale de l'Union astronomique internationale de 2015.
Définition
Selon la note 4 de la résolution B2 adoptée lors de l'assemblée générale de l'Union astronomique internationale de 2015, « le parsec est défini comme [valant] exactement 648 000π unités astronomiques »[N 1] - [10].
Interprétation géométrique de cette valeur
La nouvelle définition correspond au rayon d'un cercle dont l'arc, soutenu par un angle au centre d'une seconde d'arc, mesure exactement une unité astronomique.
Démonstration que l'interprétation géométrique correspond à cette valeur
Avec la nouvelle définition, un demi-cercle (arc de cercle d'un support angulaire de π radians) d'un parsec de rayon a une longueur de π parsecs, soit exactement 648 000 unités astronomiques. π radians étant strictement égaux à 648 000 secondes d'arc, l'arc de cercle soutenu par un angle d'une seconde d'arc mesure exactement une unité astronomique.
Interprétation physique et lien avec la définition historique
La définition actuelle (2015) donne une valeur exacte au parsec en termes d'unités astronomiques (l'unité astronomique a été définie exactement en 2012 en unités du Système international), mais la définition officielle ne donne aucune interprétation physique de celle-ci et ne la relie pas à la définition historique.
- Différence avec la définition historique
L’ancienne définition (voir la figure plus haut) signifiait qu'un parsec avait une longueur de ua, avec .
Ainsi, , ce qui donne une différence avec la nouvelle définition de (environ 200 km).
Équivalences
L'unité astronomique (ua) étant exactement définie dans le Système international comme valant 149 597 870 700 mètres (résolution de l'UAI de 2012), un parsec vaut exactement (96 939 420 213 600 000/π) mètres, soit environ 3,085 677 581 × 1016 m[10].
L'année-lumière (al) étant également définie exactement dans le Système international (1 al = 365,25 j × 86 400 s/j × 299 792 458 m/s = 9 460 730 472 580 800 m), un parsec vaut exactement (96 939 420 213 600 000/(9 460 730 472 580 800 π)) années-lumière, ce qui se simplifie en (10 246 429 500/(999 992 651 π)) années-lumière, soit environ 3,261 56 al.
Pour récapituler :
- 1 parsec = 648 000π unités astronomiques ≈ 206 264,806 247 ua ;
- 1 pc = 96 939 420 213 600 000π mètres ≈ 3,085 677 581 × 1016 m ;
- 1 pc = 96 939 420 213 600 0009 460 730 472 580 800 π années-lumière ≈ 3,261 563 777 al.
Notation
Le symbole du parsec est pc[2] - [3] - [11]. Ses multiples et sous-multiples utilisent les préfixes du Système international d'unités : kpc pour le kiloparsec (1 000 parsecs), Mpc pour le mégaparsec (un million de parsecs), Gpc pour le gigaparsec (un milliard de parsecs).
Usage
Cette unité résulte de l’application d’une méthode trigonométrique dite « méthode de la parallaxe », servant à déterminer la distance séparant un observateur d’un objet éloigné quelconque, à la mesure de la distance des objets célestes. Pour des raisons pratiques, les astronomes expriment souvent les distances des objets astronomiques en parsecs plutôt qu’en années-lumière. Cette unité permet une conversion directe des valeurs observées en distance : si la parallaxe annuelle d’une étoile est mesurée en secondes d’arc, alors la distance entre cette étoile et le Soleil, exprimée en parsecs, est égale à l’inverse de cette valeur. La magnitude absolue et le module de distance sont deux unités dérivées du parsec, et l'expression des distances en parsecs facilite la manipulation de ces données.
Les premières mesures de distance interstellaire (l’étoile 61 Cygni par Friedrich Wilhelm Bessel en 1838) furent effectuées en utilisant la largeur de l’orbite terrestre comme référence. Le parsec dériva de cette méthode. La détermination des distances des corps célestes est l’objet principal de l’astrométrie.
L’étoile la plus proche du Soleil, α Cen C (Proxima Centauri), se trouve à 1,316 parsec (4,28 années-lumière). Les distances des autres objets célestes n’appartenant pas au Système solaire sont bien plus grandes et se mesurent couramment en kiloparsecs (symbole kpc) ou mégaparsecs (symbole Mpc).
Les parallaxes ont des valeurs faibles : 0,76″ pour Proxima Centauri ; aussi, la méthode parallactique ne permet guère de déterminer des distances stellaires supérieures à cent parsecs environ, ce qui correspond à des mesures de parallaxe inférieures à dix millisecondes d’arc.
Entre 1989 et 1993, le satellite Hipparcos, lancé par l’Agence spatiale européenne, a mesuré la parallaxe d’environ cent mille étoiles avec une précision supérieure à la milliseconde d’arc, ce qui a permis de déterminer la distance d’étoiles éloignées de nous de plus d’un kiloparsec.
Calcul de la valeur d'un parsec
Selon une possible interprétation de la définition historique
Sur la figure 1, (d’échelle très réduite et ne respectant pas les valeurs angulaires), S est le Soleil, T la Terre et P un objet situé à un parsec du Soleil : par définition, l’angle est égal à une seconde d’arc (1″) et la distance TS vaut une unité astronomique (1 ua). Grâce aux règles de trigonométrie, il est possible de calculer SP :
- 1 pc 206 264,806 245 48 ua.
Comme[12]
- 1 ua = 1,495 978 707 × 1011 m,
on a :
- 1 pc 206 264,806 245 48 × 1,495 978 707 × 1011 m
donc :
- 1 pc 3,085 677 581 467 2 × 1016 m
c'est-à-dire :
- 1 pc 30 856 775 814 672 000 m.
Le choix d'une définition arbitraire mais désormais fixe de l'unité astronomique explique la précision des valeurs précédentes.
Approximations utiles
Sur le schéma ci-dessus, l'angle censé être d'une seconde a une valeur bien supérieure, et par conséquent l'hypoténuse est clairement plus longue que le côté adjacent. En réalité, pour un angle aussi petit, la différence de longueur entre les deux est très faible en valeur relative, et finalement l'hypoténuse vaut à peine plus d'un parsec (autrement dit, un parsec est aussi bien la distance du Soleil à l'étoile lointaine que de la Terre à l'étoile lointaine).
Pour les très faibles valeurs d'angles (exprimés en radians), on peut faire l'approximation (développement limité au premier ordre) ; de même , d'où l'affirmation suivant laquelle le côté adjacent et l'hypoténuse sont quasiment égaux. Dans le cas du parsec, x valant , l'erreur relative commise en confondant les deux côtés est inférieure à , donc on commet (en utilisant ces formules) une erreur de l'ordre de la distance Paris-Brest, ce qui peut sembler important, mais est évidemment négligeable aux échelles astronomiques considérées.
Notes et références
Notes
- Traduction de l'anglais « The parsec is defined as exactly (648 000/π) au ».
Références
- Informations lexicographiques et étymologiques de « parsec » dans le Trésor de la langue française informatisé, sur le site du Centre national de ressources textuelles et lexicales (consulté le ).
- Entrée « parsec », sur TERMIUM Plus, la banque de données terminologiques et linguistiques du gouvernement du Canada (consulté le ).
- (en) Entrée « parsec (pc) », dans Mohammad Heydari-Malayeri, An Etymological Dictionary of Astronomy and Astrophysics [« Un dictionnaire étymologique d'astronomie et d'astrophysique »], Paris, Observatoire de Paris, 2005-2015.
- Frédéric Arenou, « La naissance du parsec », L'Astronomie, vol. 124, no 23, , p. 20-23 (Bibcode 2010LAstr.124...20A, lire en ligne, consulté le ).
- (de) Hermann Kobold, Der Bau des Fixsternsystems, Brunswick, Friedrich Vieweg und Sohn, coll. « Wissenschaft » (no 11), , XI-256 p. (OCLC 2114301), p. 74.
- (en) Frank Watson Dyson, « The Distribution in Space of the Stars in Carrington's Circumpolar Catalogue », Monthly Notices of the Royal Astronomical Society, vol. 73, , p. 334-342 (Bibcode 1913MNRAS..73..334D, lire en ligne [[GIF]], consulté le ).
- (en) « Meeting of the Royal Astronomical Society (Friday, 1913, March 14) », The Observatory, vol. 36, , p. 160-174 (Bibcode 1913Obs....36..160, lire en ligne [[GIF]], consulté le ).
- Site researchgate.net, page sur la naissance du Parsec.
- (en) W. W. Campbell et Joel Stebbins, « Report on the Organization of the International Astronomical Union », Proceedings of the National Academy of Sciences of the United States of America, vol. 6, no 6, , p. 349- (360-361) (DOI 10.1073/pnas.6.6.349, Bibcode 1920PNAS....6..349C, lire en ligne [PDF], consulté le ).
- Note 4 de la Résolution B2 adoptée par l'Union astronomique internationale lors de sa 29e assemblée générale, , Honolulu (Hawaï, États-Unis).
- (en) Entrée « parsec », sur Oxford Reference d'Oxford University Press (consulté le ).
- Résolution B2 sur la redéfinition de l'unité astronomique de longueur, XXVIIe Assemblée générale de l'Union astronomique internationale, Pékin (Chine), : lire en ligne[PDF].










