Proportionnalité
En mathématiques, on dit que deux suites de nombres sont proportionnelles quand, en multipliant (ou en divisant) par une même constante non nulle, les termes de l'une on obtient les termes de l'autre. Le facteur constant entre l'une et l'autre de ces suites est appelé coefficient de proportionnalité. Ces suites de nombres étant par exemple des grandeurs mesurées.
Exemple : dans un magasin, le prix des pommes est de 2 euros le kilogramme. Il y a proportionnalité entre la somme S à payer et le poids P de pommes achetées, avec un coefficient de proportionnalité égal à 2.
- pour 1 kg, on doit payer 2 euros ;
- pour 3 kg, on doit payer 6 euros ;
- pour 1,5 kg, on doit payer 3 euros ;
- pour 5 kg, on doit payer 10 euros ;
- pour 10 kg, on doit payer 20 euros,
- le quotient est constant et est égal au coefficient de proportionnalité : .
Les Anciens comme Euclide auraient écrit que 2 est à 1 comme 6 est à 3 ou comme 3 est à 1,5.
La proportionnalité peut être représentée par le symbole ∝, « I ∝ V » signifiant « I est proportionnel à V ».
Tableau de proportionnalité
Un tableau de proportionnalité est un tableau où chaque ligne est proportionnelle aux autres. C'est une manière d'organiser les données qui permet de reconnaître les situations de proportionnalité, de déterminer le coefficient de proportionnalité et d'utiliser la loi proportionnelle. C'est un outil qui est a été très utilisé en didactique des mathématiques, notamment dans les années 70[1] ; en France, il est utilisé, parmi d'autres outils de proportionnalité, dès le cycle 3 (CM1, CM2, 6e)[2].
Utilisation du tableau
On dispose de deux séries de valeurs qui se correspondent, typiquement :
- une quantité achetée et le prix payé ;
- la durée d'un parcours et la distance parcourue.
Pour construire le tableau, on met simplement les séries de valeurs en ligne, l'une au dessus de l'autre. Dans l'idéal, on classe les valeurs par ordre croissant pour une des séries.
Prenons les deux exemples suivants :
| Quantité achetée (kg) | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| Prix payé (€) | 4 | 8 | 12 | 16 | 20 |
| Durée du trajet (min) | 10 | 20 | 30 | 40 | 50 |
|---|---|---|---|---|---|
| Distance parcourue (km) | 1 | 2 | 3 | 4 | 5 |
On constate que les séries de valeurs sont toutes les deux croissantes d'une part, et d'autre part que l'on peut passer d'une ligne à l'autre en multipliant ou en divisant par un nombre simple. On peut donc identifier une situation de proportionnalité et calculer le coefficient de proportionnalité : prix unitaire de 4 €/kg pour les tomates, 10 min/km pour la randonnée. Le coefficient peut être indiqué à côté du tableau :
| ↓ × 4 | ↑ ÷ 4 | Quantité achetée (kg) | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|---|---|
| Prix payé (€) | 4 | 8 | 12 | 16 | 20 |
| ↓ ÷ 10 | ↑ × 10 | Durée du trajet (min) | 10 | 20 | 30 | 40 | 50 |
|---|---|---|---|---|---|---|---|
| Distance parcourue (km) | 1 | 2 | 3 | 4 | 5 |
Il est alors possible de résoudre des problèmes du type : « J'ai 10 €, quelle quantité de tomates puis-je acheter ? » « J'ai besoin de 0,5 kg de tomates, combien cela va-t-il me coûter ? » « Quelle distance parcourt-on en une heure (60 min) ? »
| ↓ × 4 | ↑ ÷ 4 | Quantité achetée (kg) | 1 | 2 | 3 | 4 | 5 | ? | 0,5 |
|---|---|---|---|---|---|---|---|---|---|
| Prix payé (€) | 4 | 8 | 12 | 16 | 20 | 10 | ? |
| ↓ ÷ 10 | ↑ × 10 | Durée du trajet (min) | 10 | 20 | 30 | 40 | 50 | 60 |
|---|---|---|---|---|---|---|---|---|
| Distance parcourue (km) | 1 | 2 | 3 | 4 | 5 | ? |
Réponses :
- avec 10 €, on peut acheter 10 ÷ 4 = 2,5 kg ;
- l'achat de 0,5 kg de tomates va coûter 0,5 × 4 = 2 € ;
- en une heure (60 min), on parcourt 60 ÷ 10 = 6 km, la vitesse est donc de 6 km/h.
Manipulations du tableau
Considérons le tableau suivant :
| Quantité | 1 | 3 | 1,5 |
|---|---|---|---|
| Prix | 2 | 6 | 3 |
On peut ajouter une colonne à un tableau de proportionnalité en additionnant deux colonnes : 3 + 1,5 = 4,5 et 6 + 3 = 9, donc
| Quantité | 1 | 3 | 1,5 | 4,5 |
|---|---|---|---|---|
| Prix | 2 | 6 | 3 | 9 |
On peut aussi multiplier une colonne par une constante : 3 × 2 = 6 et 6 × 2 = 12, donc
| Quantité | 1 | 3 | 1,5 | 6 |
|---|---|---|---|---|
| Prix | 2 | 6 | 3 | 12 |
Si l'on choisit deux colonnes, le produit des nombres situés dans une diagonale est égal au produit des nombres situés dans l'autre diagonale (produits en croix) :
| 3 | 1,5 |
| 6 | 3 |
3 × 3 = 6 × 1,5
Quatrième proportionnelle
La quatrième proportionnelle est le quatrième nombre à mettre dans un tableau de proportionnalité dont 3 cases sont déjà remplies. Ce quatrième nombre s'obtient en faisant le produit des nombres situés sur une même diagonale et en divisant par le troisième nombre.
Cette technique est appelée « règle de trois » ou « produit en croix ».
Exemple : on considère qu'un nombre de pages est proportionnel au nombre d'heures passées à les écrire. S'il faut 6 heures pour écrire un rapport de 33 pages, combien d'heures faut-il pour écrire un rapport de 55 pages ?
Tableau de proportionnalité :
| 33 | 55 |
| 6 | ? |
Réponse :
Représentation graphique
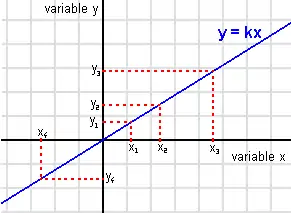
Les deux suites de valeurs sont notées (x1, x2, …, xn) et (y1, y2, …, yn). Considérons que ces valeurs soient les coordonnées de points dans un plan euclidien muni d'un repère cartésien, les valeurs x étant les abscisses et les valeurs y les ordonnées. Les coordonnées du point M1 sont (x1, y1), M2(x2, y2), Mn(xn, yn).
Si nous sommes dans une situation proportionnelle, alors les points M1, M2, …, Mn sont alignés sur une droite (D) et cette droite passe par l'origine O du repère — point de coordonnées (0, 0).
Par extrapolation, une nouvelle mesure donnerait un couple (x, y) qui correspondrait aux coordonnées d'un point de la droite (D).
Il existe un réel k tel que tous les points de (D) sont exactement les points de coordonnées (x,k × x). Autrement dit, un couple (x, y) correspond aux coordonnées d'un point de (D) si et seulement si y = k × x. Le réel k est la pente de la droite, également appelé coefficient directeur de la droite. C'est aussi le coefficient de proportionnalité de y par rapport à x. On dit aussi que y ou y(x) est une fonction linéaire de x.
Lors d'une expérience, il se peut que des erreurs soient commises lors des relevés des mesures x et y. Les points O, M1, …, Mn placés dans le graphique se retrouvent alors à proximité d'une droite, de pente k. Une certaine liberté de choix demeure sur la pente k, mais des choix en un sens meilleurs peuvent être faits, en utilisant des méthodes dites de régression linéaire.
Proportionnalité et géométrie
La proportionnalité en géométrie est principalement utilisée dans le théorème de Thalès et dans les triangles semblables. Mais on la retrouve aussi dans les coordonnées de vecteurs colinéaires. En dimension 2, la proportionnalité des coordonnées se traduit par l'égalité des produits en croix ab' = ba' qui devient alors ab' - ba'= 0 (déterminant nul).
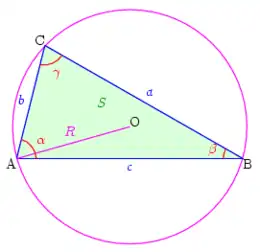
En géométrie plane, la loi des sinus affirme une relation de proportionnalité entre les longueurs et les sinus des angles d'un triangle. Sa démonstration repose sur la règle du produit en croix. Soit ABC un triangle du plan euclidien. Les longueurs des segments [BC], [CA] et [AB] sont notés a, b et c respectivement. On note , et les mesures des angles en A, B et C. Les notations sont indiquées sur la figure ci-contre. La longueur h de la hauteur issue de A peut se calculer de deux manières. Si H est le projeté orthogonal de A sur la droite (BC), les relations métriques dans les triangles rectangles ABH et ACH donnent : .
Le calcul des longueurs des autres hauteurs donne de même : et .
La règle du produit en croix implique que (a,b,c) est proportionnel a (loi des sinus). Cette loi est énoncée sous la forme .
Dans le traité de géométrie d'Euclide, deux triangles ABC et A'B'C' du plan euclidien sont définis comme semblables s'ils ont mêmes mesures d'angles. La loi des sinus implique alors que les longueurs AB, BC, et CA sont proportionnelles à A'B', B'C' et C'A'. La condition « être semblables » équivaut à l'existence d'une similitude du plan euclidien envoyant ABC sur A'B'C'. La similitude multiplie toutes les longueurs par un même coefficient k appelé le rapport de la similitude. Il vaut le coefficient de proportionnalité entre les longueurs (AB, BC, CA) et (A'B', B'C', C'A').
En géométrie vectorielle, deux vecteurs v et w d'un même espace vectoriel E sont dits colinéaires s'il existe un scalaire a tel que v=aw. Posons leurs coordonnées dans une base de E : et .
Alors les vecteurs v et w sont colinéaires ssi (v1, …, vn) est proportionnel à (w1, …, wn).
Quantités inversement proportionnelles
Deux quantités sont inversement proportionnelles[3], si l'une est proportionnelle à l'inverse de l'autre. Cette condition équivaut à ce que leur produit soit constant.
Exemple : pour parcourir 100 km, le temps est inversement proportionnel à la vitesse.
- À 100 km h−1, il faut 1 h
- À 50 km h−1, il faut 2 h
- À 10 km h−1, il faut 10 h
Leur produit est constant et représente la distance parcourue : 100 km h−1 × 1 h = 50 km h−1 × 2 h = 10 km h−1 × 10 h = 100 km
Notes et références
- Magali Hersant, « La proportionnalité dans l'enseignement français obligatoire en France, d'hier à aujourd'hui », Repères-Irem, no 59, , p. 5-41 (lire en ligne), p. 18.
- « La proportionnalité au cycle 3 », sur eduscol.education.fr, 2021 (dernière modification), p. 2.
- Petite encyclopédie des mathématiques, éditions Didier, p. 42.
Voir aussi
Articles connexes
Liens externes
- Alaeddine Ben Rhouma, « Master : Autour de la proportionnalité », INSMI, sur HAL,















