Fenêtre de Snell
La fenêtre de Snell (ou « cercle de Snell »[1], ou « trou optique »[2]) est un phénomène d'optique subaquatique liée aux propriétés de l'interface eau/atmosphère, Cette expression fait référence à la Loi de Snell (aussi dénommée Loi de Snell-Descartes), développée par le mathématicien et physicien néerlandais Willebrord Snell van Royen (ou Snellius), collectionneur d'instruments astronomiques et d'optiques, et passionné par les questions d'optique.


Et hors de la fenêtre (sur la gauche) c'est le fond/décor qui est réfléchi sous la surface comme s'il s'agissait d'un miroir souple et mouvant.
.jpg.webp)

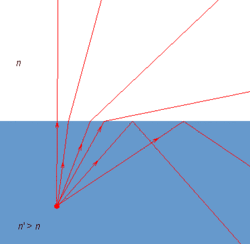
C'est le phénomène par lequel un spectateur situé à plusieurs mètres sous l'eau et regardant vers la surface ne voit ce qui est au-dessus de la surface qu'à travers un cône de perception de la lumière large d'environ 96 degrés[3]. La zone située à l'extérieur de cette « fenêtre de Snell » apparait à ce spectateur subaquatique soit complètement sombre soit réfléchit le décor subaquatique ou la partie inférieure d'objets semi-immergés.
Formation de l'image dans la fenêtre de Snell
En conditions idéales, un observateur regardant la surface de l'eau à partir du dessous et exactement au-dessus de lui verrait une image parfaitement circulaire représentant le décor d'un horizon à l'autre. En raison de la réfraction de la lumière qui se produit à la limite atmosphère/eau, la fenêtre de Snell comprime le décor visible dans un angle de vision de 180°, ce qui donne un effet similaire à celui d'un objectif fisheye de 97°. La luminosité de l'image chute brutalement à sa circonférence/horizon car la lumière incidente à des angles rasants faibles est réfléchie plutôt que réfractée (cf. équations de Fresnel).
En réalité, la réfraction est extrêmement sensible à la moindre perturbation ou irrégularités de la planéité de la surface (rides, houles, objets flottants). Ceci entraîne des distorsions locales et mouvantes de l'image voire sa désintégration complète.
De plus, dans la nature l'eau est très rarement totalement limpide ; Plus elle est turbide, plus la matière en suspension va voiler l'image dans le halo de lumière diffusée.
Biologie, écologie
Du point de vue perceptif pour les animaux marins, la fenêtre de Snell agit comme un puits de lumière[4]. Certains poissons, comme les Tylosurus, peuvent sauter en l'air avant de plonger pour bénéficier ainsi d'un effet de surprise sur leurs proies [5].
Par temps ensoleillé ou pleine lune, de nombreux animaux subaquatiques (comme la crevette Palaemonetes vulgaris étudiée de ce point de vue[4]) sont capables de percevoir des motifs de polarisation du ciel visible à travers la fenêtre de Snell, et de les utiliser pour s'orienter ou se réorienter (notamment quand le milieu est turbulent ou en période de migration), ceci bien que le motif de polarisation céleste soit perpétuellement déformé par les vagues ou les ondes de surface, et modifié à l'interface air-eau par la réfraction et la repolarisation dans le « puits de lumière »[4].
Certains phénomènes de pollution lumineuse ou des pollutions par film d'hydrocarbures peuvent négativement interférer avec ces phénomènes.
Photographie subaquatique
Le photographe sous-marine (ou en eau douce) peut exploiter ce phénomène, notamment avec un objectif grand-angle en photographiant un sujet situé « au zénith » entre le photographe et la fenêtre de Snell qui donnera un effet de rétroéclairage mettant l'accent sur le sujet, un flash permettant que ce dernier ne se découpe pas uniquement en ombre chinoise sur le fond clair de la surface. Si la surface est parfaitement claire et calme, le décor situé au-dessus de la fenêtre et à ses abords est visible (sinon sa vision est déformée par les vagues et remous).
Modélisation
Le degré et la direction de polarisation linéaire, le facteur de transmission et la forme de l'image déformée par la réfraction polarisation peuvent être calculés et modélisés en fonction de la distance du zénith du soleil (ou de la lune) et selon que le ciel soit dégagé ou plus ou moins couvert[4]. Il est ainsi possible de produire des images de synthèse crédibles pour le cinéma, des présentations pédagogiques ou pour des jeux vidéo.
Ces modèles de réfraction-polarisation peuvent aussi aider à comprendre comment les organismes animaux s'orientent et perçoivent leur environnement[4].
Notes et références
- Dave Hughes (1990). Tactics for Trout. Stackpole Books. (ISBN 0-8117-2403-4).
- David K. Lynch and William Livingstone (2001). Color and Light in Nature. Cambridge University Press. p. 79. (ISBN 0-521-77504-3)
- Martin Edge and Ian Turner (1999). The Underwater Photographer. Focal Press. (ISBN 0-240-51581-1).
- Gábor Horváth & Dezsö Varjú (1995) Underwater refraction-polarization patterns of skylight perceived by aquatic animals through Snell's window of the flat water surface ; Vision Research ; Volume 35, Issue 12, juin 1995, Pages 1651–1666 doi:10.1016/0042-6989(94)00254-J
- Recension d'un article du Journal of Fish Biology dans "Fish bring death from above", Nature, 527, 137 (12 November 2015) doi:10.1038/527137d
Voir aussi
Articles connexes
Liens externes
- Explications (en anglais) du phénomène physique qui induit la fenêtre de Snell
- Photographies subaquatiques montrant la fenêtre de Snell
Bibliographie