Racine carrée de trois

• le nombre 3 ayant deux racines carrées réelles, √3 devrait se prononcer racine carrée positive de 3, mais on le prononce simplement racine carrée de 3, voire racine de 3 pour simplifier. Il se prononçait aussi « radical de trois ».
• √3 se note également 3^1/2 : Trois puissance un demi (notation Unicode : 3^½).
• Dans les langages informatiques, il s'écrit en général sqrt(3).

${\displaystyle {\sqrt {3}}=1,7320508\cdots }$ ; ses décimales forment la suite A002194 de l'OEIS.

On conjecture que √3 est un nombre normal, à savoir que toute suite finie de décimales consécutives (ou séquence) apparaît avec la même fréquence limite que n'importe laquelle des séquences de même longueur.

Construction de la suite ${\displaystyle (u_{n})}$ ; les termes d'indice pair croissent vers √3 , ceux d'indice impair décroissent vers √3.

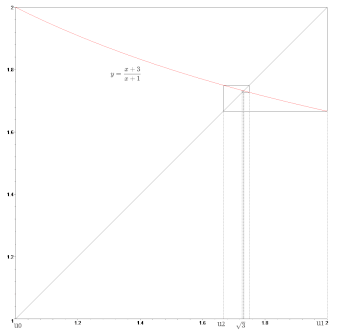
Le développement en fraction continue simple de √3 est ${\displaystyle 1+{\frac {1}{1+{\frac {1}{2+{\frac {1}{1+{\frac {1}{2+\ldots }}}}}}}}=[1,1,2,1,2,\dots ]=[1,{\overline {1,2}}]}$.

Comme pour tout irrationnel quadratique (solution d'une équation de degré 2 à coefficients entiers), ce développement est périodique. La période est de longueur 2.

Les premières réduites sont ${\displaystyle 1,2,5/3,7/4,19/11,26/15,71/41,97/56}$ (cette dernière réduite étant la bonne approximation mentionnée ci-dessus).

Elles forment la suite ${\displaystyle (u_{n})}$ définie par ${\displaystyle u_{0}=1,u_{n+1}={\frac {u_{n}+3}{u_{n}+1}}}$.

On a : ${\displaystyle u_{n}={\sqrt {3}}{\frac {(1+{\sqrt {3}})^{n+1}+(1-{\sqrt {3}})^{n+1}}{(1+{\sqrt {3}})^{n+1}-(1-{\sqrt {3}})^{n+1}}}}$, et pour ${\displaystyle n\geqslant 2}$, ${\displaystyle u_{n}={\frac {\left\lfloor (1+{\sqrt {3}})^{n+1}\right\rceil }{\left\lfloor {\frac {(1+{\sqrt {3}})^{n+1}}{\sqrt {3}}}\right\rceil }}}$ où ${\displaystyle \left\lfloor x\right\rceil }$ est l'entier le plus proche de ${\displaystyle x}$.

Archimède connaissait l'encadrement ${\displaystyle u_{8}={\frac {265}{153}}<{\sqrt {3}}<{\frac {1351}{780}}=u_{11}}$[2] - [3].

Les numérateurs forment la suite A002531 de l'OEIS et les dénominateurs la suite A002530 de l'OEIS.

Représentation de la suite des réduites de √3.

La suite de Héron convergeant vers √3 est définie par ${\displaystyle v_{0}=1,v_{n+1}={\frac {v_{n}+3/v_{n}}{2}}}$. Elle prend la valeur ${\displaystyle {\frac {97}{56}}}$ dès le terme d'indice 2.

Les numérateurs forment la suite A002812 de l'OEIS, et les dénominateurs la suite A071579 de l'OEIS.

Elle est une sous-suite de ${\displaystyle (u_{n})}$ : ${\displaystyle v_{n}=u_{(2^{n}-1)}}$ , décroissant rapidement vers √3 (convergence quadratique). Une suite croissante associée est ${\displaystyle (3/v_{n})}$, d'où l'encadrement: ${\displaystyle 3/v_{n}<{\sqrt {3}}<v_{n}}$. Pour ${\displaystyle n=4}$, cet encadrement permet déjà d'obtenir ${\displaystyle {\sqrt {3}}\approx 1,73205081}$.

${\displaystyle {\sqrt {3}}=\sum _{n=0}^{\infty }{\frac {\binom {2n}{n}}{6^{n}}}}$ ; voir à Coefficient binomial central, Série génératrice.

• ${\displaystyle 1+{\sqrt {3}}={\sqrt {2+2{\sqrt {2+2{\sqrt {2+\cdots }}}}}}}$ ; voir à Radical_imbriqué#Racine_carrée,
• ${\displaystyle {\sqrt {3}}={\sqrt[{3}]{3{\sqrt[{3}]{3{\sqrt[{3}]{3\dots }}}}}}}$ car ${\displaystyle {\frac {1}{3}}+{\frac {1}{3^{2}}}+{\frac {1}{3^{3}}}+\cdots ={\frac {1}{2}}}$.

La valeur √3 est atteinte par plusieurs fonctions trigonométriques :

${\displaystyle {\sqrt {3}}=\tan {\frac {\pi }{3}}=\cot {\frac {\pi }{6}}=2\sin {\frac {\pi }{3}}=2\cos {\frac {\pi }{6}}}$.

• √3 est un entier quadratique (entier algébrique de degré 2)

• Les racines cubiques de l'unité sont

${\displaystyle 1,\quad (-1+{\rm {i}}{\sqrt {3}})/2\quad {\rm {et}}\quad (-1-{\rm {i}}{\sqrt {3}})/2.}$

• La diagonale d'un cube de côté 1 mesure √3.

• La hauteur d'un triangle équilatéral de côté 1 est égale à √3/2. Ceci donne un moyen de construction de √3 à la règle et au compas. Cette propriété entraîne les suivantes :
  • l'aire d'un triangle équilatéral de côté 1 vaut √3/4 ; l'aire latérale d'un tétraèdre régulier de côté 1 vaut donc √3.
  • la distance entre deux côtés opposés d'un hexagone régulier de côté 1 est égale à √3 ;
  • √3 est le rapport des longueurs des diagonales d'un losange d'angles 60° et 30°.
  • √3 est le rapport entre la plus grande largeur et la plus petite largeur de la figure Vesica piscis.
    • 
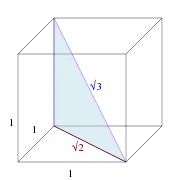      Diagonale d'un cube unité.
    • 
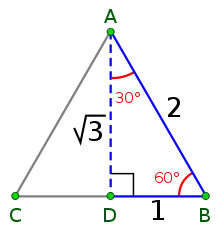      Proportions entre le côté d'un triangle équilatéral et sa hauteur.
    • 
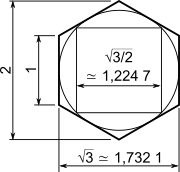      Hexagone avec ses cotes.
    • 
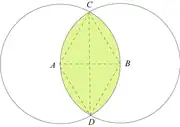      Vesica piscis avec son losange 30°/60° inscrit : ${\displaystyle CD/AB={\sqrt {3}}}$.

• Somme quadratique de Gauss
• Racine carrée de deux
• Racine carrée de cinq