Théodore de Cyrène

La vie de Théodore de Cyrène nous est mal connue. On sait qu'il naquit et mourut à Cyrène, mais qu'il ne passa pas toute sa vie dans sa ville natale et fit de fréquents séjours à Athènes. On croit qu'il fut un disciple de Protagoras. Il est possible qu'il ait été le maître en mathématique de Théétète d'Athènes, peut-être de Socrate[1], voire de Platon.

En plus de ses travaux en mathématiques, il s’intéressait à l’astronomie, à la musique et à toutes les disciplines touchant l’enseignement. C’était un pythagoricien convaincu et un des principaux philosophes de l’école de Cyrène. Cicéron le range parmi les athées[2]. Il pensait que le plaisir et la douleur ne correspondaient ni au Bien, ni au Mal et que pour être heureux, il suffisait de savoir être « sage ».

Spirale d'Anderhub, dite de Théodore de Cyrène, pour obtenir les racines carrées de 2 à 17. On part du triangle rectangle dont les côtés valent 1 et, selon la formule de Pythagore, l'hypoténuse √2. Laquelle forme un côté d'un nouveau triangle rectangle dont l'autre côté mesure 1 et, selon la même formule, l'hypoténuse √3. Ainsi de suite.

Dans le domaine des mathématiques, il s’intéressa aux nombres irrationnels, comme Platon en témoigne dans le dialogue du Théétète en 147 d. Théodore et les mathématiciens contemporains étudièrent plusieurs cas d’incommensurabilité à partir de celui qui correspond à la ${\displaystyle {\sqrt {3}}}$, ce qui présuppose que le cas correspondant à la ${\displaystyle {\sqrt {2}}}$ était déjà connu[3]. Il démontra que les racines carrées des nombres entiers non carrés jusqu'à 17 (c'est-à-dire : 3, 5, 6, 7, 8, 10, 11, 12, 13, 14, 15 et 17) étaient des nombres irrationnels. Mais aucune indication ne subsiste sur la méthode qu’il utilisa[4].

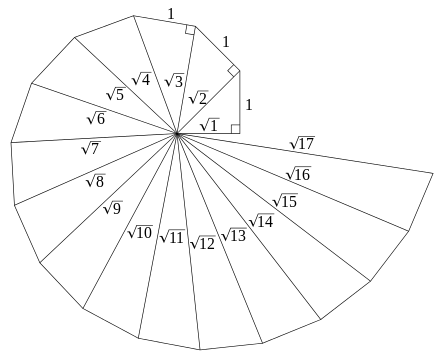
En 1941, Jakob Heinrich Anderhub a imaginé la construction d'une spirale composée de 16 triangles rectangles donnant les racines des nombres entiers de 2 à 17[5]. Depuis, cette construction a été nommée spirale de Théodore mais on ne sait pas si c'est la méthode utilisée par Théodore de Cyrène.

Au début du XX^e siècle, Hieronymus Georg Zeuthen a suggéré que Théodore aurait pu utiliser l'algorithme d'Euclide[6].

Cependant Nicolas Bourbaki écrit[7] :

« On s'accorde, sur le témoignage de Platon dans son Théétète, à attribuer à Théodore de Cyrène la démonstration de l'irrationalité de √3 , √5, « et ainsi de suite jusqu'à √17 »[8], à la suite de quoi Théètète aurait, soit obtenu une démonstration générale pour √N (N = entier non carré parfait), soit en tout cas (si, comme il se peut, la démonstration de Théodore était générale dans son principe) procédé à une classification de certains types d'irrationnels. On ne sait pas si ces premières démonstrations d'irrationalité procédaient par voie arithmétique ou géométrique. »

• Luc Brisson (dir.) (trad. du grec ancien par Michel Narcy), Théétète : Platon, Œuvres complètes, Paris, Éditions Flammarion, 2008 (1^re éd. 2006), 2204 p. (ISBN 978-2-08-121810-9). 
• G.E.R. Lloyd (en), « La démonstration et l’idée de science », dans Jacques Brunschwig et Geoffrey Lloyd, Le savoir grec, Paris, Flammarion, 1996, p. 282-283. 

• (en) John J. O'Connor et Edmund F. Robertson, « Theodorus of Cyrene », sur MacTutor, université de St Andrews.

• Ressource relative aux beaux-arts :
  • (de + en + la) Sandrart.net
• Notices dans des dictionnaires ou encyclopédies généralistes :

  • Deutsche Biographie
  • Enciclopedia De Agostini
  • Universalis
• Notices d'autorité :

  • VIAF
  • ISNI
  • IdRef
  • LCCN
  • GND
  • WorldCat