Lewis Fry Richardson
Lewis Fry Richardson (1881-1953) est un mathématicien, météorologiste et psychologue britannique. Au cours des années 1916-1918, il imagina de prévoir le temps à partir des équations primitives atmosphériques, les lois de la mécanique des fluides qui régissent les mouvements de l'air.

| Naissance | |
|---|---|
| Décès | À Argyll |
| Nationalité | |
| Domicile | |
| Formation |
Bootham School (en) (- Université de Newcastle upon Tyne (- King's College (- |
| Activités | |
| Parentèle |
Ralph Richardson (neveu) Julian Hunt (petit-neveu) William Garnett (en) (beau-père) |
| A travaillé pour |
University of Paisley (en) (- Westminster College (en) (- Met Office (- Friends' Ambulance Unit (- Met Office (- Université de Manchester (- National Physical Laboratory (- Université d'Aberystwyth (- National Physical Laboratory (- University of Manchester Institute of Science and Technology (en) |
|---|---|
| Membre de | |
| Maître | |
| Influencé par |
Extrapolation de Richardson, modified Richardson iteration (d), nombre de Richardson |
Enfance
Richardson est né en 1881 à Newcastle-upon-Tyne — un port industriel du nord de l'Angleterre — dans une famille de quakers. On l'envoya à l'école de Bootham, ayant cette affiliation, comme pensionnaire, et il y développa son goût pour la science et l'histoire naturelle. À 19 ans, il entra au King's College (Cambridge) où il obtint une licence ès sciences physiques. Il eut comme directeur Joseph John Thomson, Prix Nobel de physique, pour sa spécialisation en physique et mathématique.
Il entra au National Physical Laboratory après ses études et enseigna au University College d'Aberystwyth (Pays de Galles)[1]. Il travailla également pour l'industrie et enseigna plus tard au Manchester College of Technology. Durant les dix premières années de sa carrière, il développa des techniques mathématiques pour la résolution approchée d’équations différentielles non-linéaires ou couplées[1]. Il les appliqua au problème de la résolution des équations de la physique de l'atmosphère en espérant en tirer une méthode pratique.
En 1913, Richardson déménagea au Eskdalemuir Observatory en Écosse et devint directeur de l'observatoire de météorologie et de relevés magnétiques, une branche du Met Office. Il y continua ses recherches sur la prédiction du temps. En 1916[1], en tant que quaker, opposé à prendre les armes[2], il s'engage dans le corps des ambulanciers en France (Friends' Ambulance Unit). Il profita alors de son temps libre pour parfaire ses idées et les écrivit dans un manuscrit qu'il faillit perdre.
De retour en Angleterre en 1919[1], Richardson retourna au Met’ Office à une station expérimentale près d’Oxford où il travailla sur les turbulences de l'air. Ceci l’amena à développer un critère pour qualifier la turbulence qu'on nomme le nombre de Richardson. Quand le Met’Office fut placé sous la direction du Ministère de l'Air, Richardson remit sa démission en raison de ses convictions quakers et se joignit au Westminster Training College comme directeur du département de physique.
Travaux sur la prévision météorologique
Vilhelm Bjerknes avait proposé dès 1904[3] que l'atmosphère obéissait à un ensemble de variables qu'on pouvait relier sous forme d'équations qu'il pensait résolubles. Richardson essaya donc de montrer que le calcul permettrait effectivement d'effectuer des prévisions météorologiques, à une époque où les calculateurs électroniques n'existaient pas encore. Il publia sa méthode en 1922, à peine trois ans après que fut publiée la théorie des fronts météorologiques et de la cyclogénèse des latitudes moyennes par Vilhelm et Jacob Bjerknes. Richardson préconisait des techniques de calcul permettant de simplifier les équations et indiquait qu'il était nécessaire de partir d'une situation météorologique avec un nombre important de données terrestres et d'altitude sur l'ensemble du globe.
À l'aide de formulaires standardisés, pour accélérer le calcul en divisant le travail, il avait estimé que 64 000 personnes[4] étaient nécessaires pour que la prévision soit émise en avance sur les événements. Richardson découpait le globe en une grille rectangulaire de 230 km (en latitude) sur 200 km (en longitude)[4], ce qui donnait 3 200 colonnes verticales autour de la Terre. De plus, il divisait l'atmosphère en tranche à 4, 7 et 12 km d'altitude et il proposait des calculs par pas de temps de 3 heures[4]. Cet immense système a été baptisé « l’usine à prévoir le temps. »
Cependant, un petit essai de prévision d'évolution de la pression atmosphérique selon cette méthode, mais sans tout le personnel, donna un résultat très décevant: la variation calculée était de 145 hPa en 6 heures, une valeur tout à fait impossible quand on pense qu'une variation de 20 hPa est considérée comme une variation extrême pour une telle durée d'observation ; de fait, la variation mesurée était presque nulle. L'erreur de Richardson a été de discrétiser les dérivées des équations primitives atmosphériques sans tenir compte de la variabilité expérimentale des données[2].
Ces dérivées impliquent des divisions de nombres qui sont très proches l'un de l'autre (ex. variation de la pression ou de la température avec le temps) ; or la variation des variables météorologiques peut être de l'ordre de l'erreur de leur mesure et en plus, elle peut être instantanément grande sans pour autant durer. Il faut donc utiliser des valeurs lissées sur une certaine période pour obtenir des résultats réalistes[5]. On sait maintenant que le pas de temps n'aurait pas dû excéder une demi-heure dans les calculs et que les données initiales[2], n'ayant pas subi de contrôle de qualité, introduisirent des instabilités de calcul. Richardson a cependant démontré l'idée que la prévision du temps par calcul était possible et les problèmes de logistique humaine et financière ont été résolus plus tard par l'avènement des ordinateurs.
Un peu plus de vingt ans plus tard, en 1946, le météorologiste Jule Charney assista à la conférence de Princeton, organisée par John von Neumann, sur « la météorologie dynamique et le calcul électronique automatique à grande vitesse », avant de travailler avec Arnt Eliassen, Eric Eady et Ragnar Fjortoff sur les équations atmosphériques. Charney émit, en 1948, les hypothèses (vent horizontal quasi géostrophique et pression quasi hydrostatique) permettant de construire le premier modèle de prévision atmosphérique à l'échelle synoptique, pour les latitudes moyennes et le testa avec succès, en , sur l’ENIAC, un des premiers calculateurs électroniques[6]. La machine à prévoir le temps était devenue réalité. En 1952, Jule Charney écrivit à Richardson pour lui faire part de ses travaux[7] mais celui-ci a déjà tourné la page, depuis 1926.
Changement de cap
L'usage possible de ses travaux en météorologie pour des raisons militaires fit abandonner à Richardson, à cause de ses profondes convictions pacifistes, ce domaine de recherche dès le milieu des années 1920. Il se tourna alors vers l'étude de la dynamique, des statistiques et sur les raisons de l'existence des guerres. Il avait d'ailleurs tenté de publier un premier livre, Mathematical Psychology of War, qu'il dédiait à ses camarades ambulanciers de la guerre. Ne trouvant pas de maison d'édition prête à le faire, il dut le faire lui-même en 1919[1].
À partir de 1926, il commença à collecter le plus de données possible sur la cause des conflits armés allant de la Première Guerre mondiale aux guerres de pouvoirs des gangsters de Chicago. Il obtint un diplôme en psychologie à 48 ans, devint Principal du Paisley Technical College (maintenant Université de Paisley) en 1929 et commença ses recherches sur les conflits internationaux[1]. Ceci devint son intérêt principal pour le reste de sa vie, même s'il continua à travailler occasionnellement au problème de turbulence. Après avoir touché un héritage en 1939, Richardson démissionna de ses anciennes fonctions pour se consacrer entièrement à l'analyse psychologique des guerres[2].
Comme il fit pour la météorologie, il analysa ses données à l'aide d'équations différentielles et des probabilités en considérant l’armement de deux nations et la longueur de leur frontière commune. Il mit en hypothèse que ces deux variables étaient directement proportionnelles et menaient aux frictions entre nations. Les solutions à son système d'équations est utilisable pour analyser le potentiel de conflits armés. Dans Arms and Insecurity (1949) et Statistics of Deadly Quarrels (1950), il tenta d'expliquer ses théories sur les causes statistiques des guerres.
Recherche sur les fractales
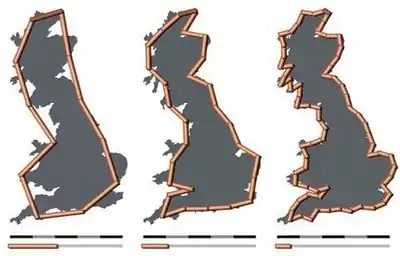
Dans le cours de ses recherches sur les conflits armés, Richardson devait calculer la longueur des frontières entre nations. Il se rendit compte que les données disponibles à ce sujet variaient grandement d'une source à l’autre. Il se mit donc à enquêter sur la cause de ces divergences: changement d'unité de mesure entre sources, méthode de mesure, etc. Il découvrit que plus l'unité minimale de mesure utilisée est petite, plus la frontière était longue ce qu'on a appelé l’effet Richardson.
Par exemple, l’image de droite montre trois mesures de la côte de Grande-Bretagne avec des étalons de mesures de plus en plus fins qui donnent des longueurs différentes. Ceci ne veut cependant pas dire que la longueur de la côte devienne infinie si on utilise une unité de mesure infiniment petite, une impossibilité quantique. Cette recherche fut généralement ignorée par la communauté scientifique à l’époque mais reprise plus tard par Benoît Mandelbrot[2] en 1967 dans son article How Long Is the Coast of Britain? (en) (Quelle est la longueur de la côte britannique ?) sur l’étude des fractales[8].
Reconnaissance
Il a été élu Fellow de la Royal Society et secrétaire de la Royal Meteorological Society. Il est l'auteur de plus de 100 publications scientifiques et de nombreux ouvrages sur les conflits. Plusieurs instituts portent son nom comme le Richardson Institute for Peace Studies et le Conflict Resolution de l'université de Lancaster[1].
Notes
- (en) Keith C. Heidorn, « L.F. Richardson: Building the forecast Factory », The Weather Doctor, .
- Benoit Mandelbrot, Les objets fractals, (1re éd. 1975), 208 p. (ISBN 978-2-08-081301-5), chap. 15 (« Esquisses biographiques »).
- (en) Wilhelm Bjerknes, « The problem of Weather Prediction, as seen from the standpoints of Mechanics and Physics », NOAA (consulté le ).
- « Richardson (Lewis Fry) » [archive du ], Glossaire, Météo-France (consulté le ).
- (en) Peter Lynch du Met Éiriann, « Richardson's forecast: What went wrong? », NOAA, — Une analyse du premier essai de prévision de Richardson.
- (en) Chester W. Newton et Eero O. Holopainen, Extratropical cyclones : the Erik Palmén memorial volume, Boston, MA, AMS, (ISBN 978-1-878220-03-5 et 1-878220-03-9, OCLC 22613555).
- Michel. Rochas, et Jean-Pierre Javelle, La météorologie : la prévision numérique du temps et du climat, Syros/Alternatives, (ISBN 2-86738-971-2 et 978-2-86738-971-9, OCLC 300226287).
- Cf. les développements dans B. Mandelbrot, Les objets fractals et Survol du langage fractal, Flammarion, coll. « Champs-Flammarion », (réimpr. 1984, 1989, 1995).
Bibliographie
- (en) Lewis F. Richardson (préf. Peter Lynch), Weather Prediction by Numerical Process, Cambridge, New York Cambridge University Press, coll. « Cambridge mathematical library », , 236 p. (ISBN 978-0-521-68044-8 et 0-521-68044-1, OCLC 150337883, lire en ligne)
- (en) John J. O'Connor et Edmund F. Robertson, « References for Archibald Richardson », sur MacTutor, université de St Andrews.
- (en) Oliver M. Ashford, Prophet--or professor? : the life and work of Lewis Fry Richardson, Bristol Boston, A. Hilger, , 304 p. (ISBN 978-0-85274-774-2 et 0-852-74774-8, OCLC 12666427).
- (en) O. M. Ashford, Collected papers of Lewis Fry Richardson, Cambridge, 1993.
- (en) E. Gold, « Lewis Fry Richardson, 1881-1953 », Obituary Notices of Fellows of the Royal Society, vol. 9, no 1, 1954, p. 217-235 DOI 10.1098/rsbm.1954.0015.
- (en) E. Gold, « Lewis Fry Richardson », Dictionary of National Biography Supp. (1951-60), Londres, 1971, p. 837-839.
- (en) A. Rapoport, « Lewis Fry Richardson », International Encyclopedia of Social Sciences, no 14, 1968, p. 513-517.
- (en) A. Rapoport, « Lewis F Richardson's mathematical theory of war », Journal of Conflict Resolution, vol 1, no 2, 1957, p. 249-299.
- (en) P. A. Sheppard (en), « Dr L. F. Richardson, F.R.S. », Nature, no 172, 1953, p. 1127-1128 DOI 10.1038/1721127a0.
- (en) John Todd (en), « Obituary: L. F. Richardson (1881-1953) », Mathematical Tables and Other Aids to Computation (Math. Comp.), vol. 8, no 48, 1954, p. 242-245 DOI 10.1090/S0025-5718-1954-0063988-7.
Voir aussi
Articles connexes
Liens externes
- Ressource relative aux beaux-arts :
- Notices dans des dictionnaires ou encyclopédies généralistes :
- « Les mouvements de l'atmosphère », Éducation, Météo-France
- Katia Chacinbault, « La prévision numérique météorologique » [PDF], Risques hydro-météorologiques, crues et inondations, Laboratoire d'études des Transferts en Hydrologie et Environnement (LTHE)