Algèbre de Heyting
En mathématiques, une algèbre de Heyting est une structure algébrique introduite en 1930 par le mathématicien néerlandais Arend Heyting pour rendre compte formellement de la logique intuitionniste de Brouwer, alors récemment développée[1]. Les algèbres de Heyting sont donc pour la logique intuitionniste analogue à ce que sont des algèbres de Boole pour la logique classique : un modèle formel permettant d'en fixer les propriétés.
Les algèbres de Heyting jouent aujourd'hui un rôle important au-delà du seul domaine de la logique, par exemple en topologie dans la théorie des locales, et en informatique théorique. Dans ce domaine, Saul Kripke a montré en 1965 que toute équation dans une algèbre de Heyting est décidable[2], et Richard Statman a précisé que le problème est PSPACE-complet en 1979[3].
Définition
Une algèbre de Heyting est un treillis borné tel que, pour tout couple d'éléments , il existe un plus grand élément qui satisfait
Cet élément est noté . Le plus grand élément de est dénoté 1 et le plus petit élément de est dénoté 0.
Pseudo-complément
Pour tout élément on définit le pseudo-complément de par . Cet élément vérifie la non contradiction : , et c'est d'ailleurs le plus grand élément de qui satisfait cette propriété. En revanche, et c'est la différence notable entre la logique intuitionniste et la logique classique, il n'est pas vrai en général que .
Il découle de l'existence de cet élément que toute algèbre de Heyting est distributive, c'est-à-dire
pour tout triplet .
Éléments réguliers
Un élément régulier est tel que . Les éléments 0 et 1 sont toujours réguliers, mais ce n'est pas le cas des autres en général. Une algèbre de Heyting dans laquelle tous les éléments sont réguliers est en fait une algèbre de Boole.
Morphismes d'algèbres de Heyting
Un morphisme d'algèbres de Heyting commute aux opérations et envoie 0 sur 0. Cette opération est associative, et les algèbres de Heyting forment donc une catégorie. On peut, réciproquement, définir une algèbre de Heyting en termes catégoriques, comme un treillis borné possédant tous les objets exponentiels. La flèche de Heyting correspond alors à l'exponentielle, et on a une adjonction entre et dans .
Exemples
- Toute algèbre de Boole est en particulier une algèbre de Heyting, où est donné par .
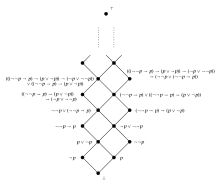
- L'ensemble des formules intuitionnistes générées par un terme est une algèbre de Heyting, on l'appelle treillis de Rieger-Nishimura.
- Dans tout espace topologique, la collection des ouverts forme une algèbre de Heyting. Dans ce cas, la flèche de Heyting est donnée par , l'intérieur de l'union du complément de et de . C'est le point de départ de la théorie des locales[4].
- L'algèbre de Lindenbaum est une algèbre de Heyting.
- Les algèbres de Łukasiewicz-Moisil sont des algèbres de Heyting[5].
Propriétés
Lois de De Morgan
On a toujours dans une algèbre de Heyting comme en logique classique. En revanche, la relation duale n'est pas satisfaite, et on a à la place une version faible : .
Notes et références
- (de) Arend Heyting, Die formalen Regeln der intuitionistischen Logik. I, II, III, Sitzungsberichte Akad. Berlin, , p 42-56, 57-71, 158-169
- (en) Saul A. Kripke, Semantical Analysis of Intuitionistic Logic I (DOI 10.1016/s0049-237x(08)71685-9, lire en ligne), p. 92–130
- (en) Richard Statman, « Intuitionistic propositional logic is polynomial-space complete », Theoretical Computer Science, vol. 9, no 1, , p. 67–72 (DOI 10.1016/0304-3975(79)90006-9, lire en ligne, consulté le )
- (en) Peter T. Johnstone, « The point of pointless topology », Bulletin (New Series) of the American Mathematical Society, vol. 8, no 1, (ISSN 0273-0979 et 1088-9485, lire en ligne, consulté le )
- (en) George Georgescu, « N-Valued Logics and Łukasiewicz–Moisil Algebras », Axiomathes, vol. 16, nos 1-2, , p. 123–136 (ISSN 1122-1151 et 1572-8390, DOI 10.1007/s10516-005-4145-6, lire en ligne, consulté le )





















