Logique classique

La sémantique (autrement dit la signification) de la logique classique se fait par des tables de vérité.

Figure 1: Contre-modèle de Kripke de ${\displaystyle (A\Rightarrow B)\vee (B\Rightarrow A)}$

Figure 2: Contre-modèle de Kripke de ${\displaystyle A\vee \neg A}$

Si on ajoute la proposition ${\displaystyle (A\Rightarrow B)\vee (B\Rightarrow A)}$ à la logique intuitionniste, on obtient une logique qui n'est plus la logique intuitionniste, car ${\displaystyle (A\Rightarrow B)\vee (B\Rightarrow A)}$ n'est pas une conséquence de la logique intuitionniste, et qui n'est pas encore la logique classique, car le tiers-exclus n'est pas une conséquence de cette formule.

Les modèles de Kripke sont essentiels pour comprendre la différence entre logique classique et logique intuitionniste. Le présent paragraphe en est une illustration et explique l'affirmation de l'alinéa ci-dessus.

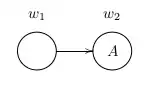
La figure 1 montre un contre modèle de Kripke ${\displaystyle {\mathcal {M}}}$ de la proposition ${\displaystyle (A\Rightarrow B)\vee (B\Rightarrow A)}$. Ça n'est pas un modèle de Kripke de ${\displaystyle (A\Rightarrow B)\vee (B\Rightarrow A)}$ parce que ${\displaystyle {\mathcal {M}},w_{1}\nvDash (A\Rightarrow B)\vee (B\Rightarrow A)}$. En effet,

${\displaystyle {\mathcal {M}},w_{2}\nvDash A\Rightarrow B}$

${\displaystyle {\mathcal {M}},w_{3}\nvDash B\Rightarrow A}$

donc

${\displaystyle {\mathcal {M}},w_{1}\nvDash (A\Rightarrow B)}$

${\displaystyle {\mathcal {M}},w_{1}\nvDash (B\Rightarrow A)}$

d'où l'affirmation ci-dessus. Par conséquent, la proposition ${\displaystyle (A\Rightarrow B)\vee (B\Rightarrow A)}$ n'est pas valide dans la logique intuitionniste.

Tous les modèles de Kripke linéaires, c'est-à-dire tous les modèles dans lesquels chaque monde a un seul autre monde accessible, sont des modèles de Kripke de ${\displaystyle (A\Rightarrow B)\vee (B\Rightarrow A)}$. C'est le cas de la figure 2. En revanche ce modèle ${\displaystyle {\mathcal {M}}'}$ n'est pas un modèle de ${\displaystyle A\vee \neg A}$, car

${\displaystyle {\mathcal {M}}',w_{1}\nvDash A}$

${\displaystyle {\mathcal {M}}',w_{1}\nvDash \neg A}$

Puisque ${\displaystyle A\vee \neg A}$ n'est pas valide dans tous les modèles de ${\displaystyle (A\Rightarrow B)\vee (B\Rightarrow A)}$, ${\displaystyle A\vee \neg A}$ ne peut pas être une conséquence de ${\displaystyle (A\Rightarrow B)\vee (B\Rightarrow A)}$. Donc plus généralement la logique classique ne peut pas être engendrée par l'ajout de ${\displaystyle (A\Rightarrow B)\vee (B\Rightarrow A)}$ à la logique intuitionniste.

Notons en passant que nous avons aussi montré que ${\displaystyle A\vee \neg A}$ n'est pas valide en logique intuitionniste.

La loi de Peirce est la proposition ${\displaystyle ((A\Rightarrow B)\Rightarrow A)\Rightarrow A}$. Elle n'est pas valide en logique intuitionniste et son ajout à celle-ci produit la logique classique. Elle a la particularité de ne contenir que des implications à la différence des quatre propositions citées plus haut qui contiennent toutes une négation.

• Rappel : Bases de : logique, ensembles, limites.
• Logique intuitionniste
• Logique minimale