Homologie (mathématiques)
En mathématiques, l'homologie[1] est une manière générale d'associer une séquence d'objets algébriques tels que des groupes abéliens ou des modules à d'autres objets mathématiques tels que des espaces topologiques. Les groupes d'homologie ont été définis à l'origine dans la topologie algébrique. Des constructions similaires sont disponibles dans beaucoup d'autres contextes, tels que l'algèbre abstraite, les groupes, les algèbres de Lie, la théorie de Galois et la géométrie algébrique.
La motivation initiale pour définir les groupes d'homologie était l'observation que deux formes peuvent être distinguées en examinant leurs trous. Par exemple, un cercle n'est pas un disque car le cercle est perforé alors que le disque est solide et la sphère n'est pas un cercle car la sphère renferme un trou bidimensionnel alors que le cercle renferme un trou unidimensionnel. Cependant, étant donné qu’un trou n’est "pas là", la définition d'un trou et comment distinguer différents types de trous n'est pas évident. L'homologie était à l'origine une méthode mathématique rigoureuse pour définir et classer les trous dans une variété. En gros, un cycle est une sous-variété fermée, une limite est un cycle qui est également la limite d'une sous-variété et une classe d'homologie (qui représente un trou) est une classe d'équivalence de cycles modulo une limite. Une classe d'homologie est donc représentée par un cycle qui n'est la limite d'aucune sous-variété: le cycle représente un trou, à savoir une variété hypothétique dont la limite serait ce cycle, mais qui "n'est pas là".
Il existe de nombreuses théories d'homologie. Un type particulier d'objet mathématique, tel qu'un espace topologique ou un groupe, peut avoir une ou plusieurs théories d'homologie associées. Lorsque l'objet sous-jacent a une interprétation géométrique, à l'instar des espaces topologiques, le n-ième groupe d'homologie représente le comportement dans la dimension n . La plupart des groupes d'homologie ou des modules peuvent être formulés en tant que foncteurs dérivés sur des catégories abéliennes appropriées, en mesurant l'incapacité d'un foncteur à être exact. Dans cette perspective abstraite, les groupes d'homologie sont déterminés par des objets d'une catégorie dérivée.
Contexte
Origines
La théorie de l'homologie commence avec la formule du polyèdre d'Euler, ou caractéristique d'Euler[2]. Viennent ensuite la définition de Riemann des invariants numériques de genre et de n-connexité en 1857 et la preuve de Betti en 1871 de l'indépendance des "nombres d'homologie" par rapport au choix de la base[3].
L'homologie elle-même a été développée pour analyser et classer des variétés en fonction de leurs cycles - boucles fermées (ou plus généralement sous-variétés) pouvant être dessinées sur une variété n dimensionnelle donnée mais ne se déformant pas continûment[4]. Ces cycles sont aussi parfois considérés comme des coupes qui peuvent être collées, ou comme des fermetures éclair qui peuvent être fermées ou non. Les cycles sont classés par dimension. Par exemple, une ligne dessinée sur une surface représente un cycle, une boucle fermée ou (1-variété), tandis qu'une surface coupée à travers une variété tridimensionnelle est un 2-cycle.
Surfaces
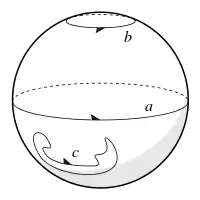
Sur la sphère ordinaire , le cycle b du diagramme peut être réduit au pôle, et même le grand cercle équatorial a peut être réduit de la même manière. Le théorème de Jordan montre que tout cycle arbitraire comme c peut être réduit de la même manière à un point. Tous les cycles de la sphère peuvent donc être transformés en permanence et appartiennent à la même classe d'homologie. On dit qu'ils sont homologues à zéro. Découper une variété le long d'un cycle homologue à zéro la sépare en deux composantes ou plus. Par exemple, découper la sphère le long de a produit deux hémisphères.
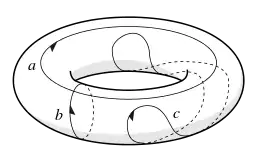
Ce n'est généralement pas le cas des cycles sur d'autres surfaces. Le tore a des cycles qui ne peuvent pas être continuellement déformés les uns dans les autres, par exemple, dans le diagramme, aucun des cycles a, b ou c ne peut être déformé l'un dans l'autre. En particulier, les cycles a et b ne peuvent pas être réduits à un point alors que le cycle c le peut, le rendant ainsi homologue à zéro.
Si la surface du tore est découpée à la fois en a et en b, elle peut être ouverte et aplatie en un rectangle ou, plus commodément, en un carré. Une paire de côtés opposés représente la coupe le long de a, et l'autre paire opposée représente la coupe le long de b .
Les bords du carré peuvent ensuite être recollés de différentes manières. Le carré peut être tordu pour permettre aux bords de se rencontrer dans la direction opposée, comme indiqué par les flèches sur le diagramme. Jusqu'à symétrie, il existe quatre manières différentes de coller les côtés, chacune créant une surface différente :
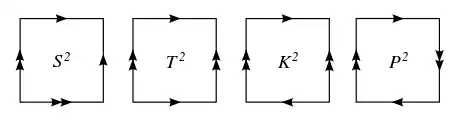
est la bouteille de Klein, qui est un tore avec une torsion (La torsion peut être vue dans le diagramme carré comme l’inversion de la flèche du bas). C'est un théorème que la surface recollée doit s'auto-intersecter (lorsqu'elle est dans un espace à 3 dimensions). Comme les tores, les cycles a et b ne peuvent pas être réduits tandis que c peut l'être. Mais contrairement au tore, suivre b en avant, à droite et en arrière retourne la gauche et la droite, car b coupe la torsion donnée à une jointure. Si une coupe équidistante d'un côté de b est réalisée, elle revient de l'autre côté et contourne une seconde fois la surface avant de revenir à son point de départ en découpant une bande de Möbius torsadée. Comme les zones de gauche et de droite locales peuvent être réorientées de manière arbitraire de cette manière, la surface dans son ensemble est dite non orientable.
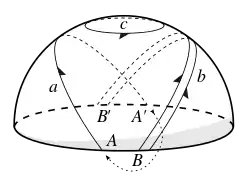
Le plan projectif a les deux jointures tordues. La forme non coupée, généralement représentée par la surface de Boy, est visuellement complexe, de sorte qu'une incorporation hémisphérique est montrée dans le diagramme, dans lequel les points antipodaux autour du bord, tels que A et A′ sont identifiés comme le même point. Encore une fois, a et b sont non-rétractables alors que c l'est. Mais cette fois, a et b inversent la gauche et la droite.
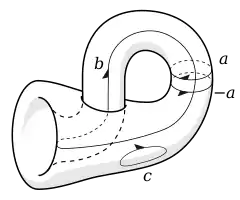
Les cycles peuvent être joints ou ajoutés ensemble, comme en a et en b sur le tore quand il était ouvert et aplati. Dans le diagramme de la bouteille de Klein, a fait le tour dans un sens et --a fait le tour dans le sens opposé. Si a est considéré comme une coupe, puis -a peut être considéré comme une opération de collage. Faire une coupe puis la recoller ne change pas la surface, donc a + (-a) = 0.
Considérons maintenant deux a-cycles. Étant donné que la bouteille de Klein est non orientable, vous pouvez transporter un d'eux tout autour de la bouteille (le long de la b-cycle), et il va revenir en -a. En effet, la bouteille de Klein est fabriquée à partir d' un cylindre, dont les extrémités a-cycle sont collées ensemble avec des orientations opposées. D'où 2a = a + a = a + (-a) = 0. Ce phénomène s'appelle la torsion. De même, dans le plan projectif, le fait de suivre le cycle insécable b deux fois crée remarquablement un cycle trivial qui peut être réduit à un point; c'est-à-dire que b + b = 0. Puisque le cycle b doit être suivi deux fois pour atteindre un cycle nul, on dit que la surface a un coefficient de torsion de 2. Cependant, le fait de suivre un cycle b deux fois dans la bouteille de Klein donne simplement b + b = 2 b, car ce cycle vit dans une classe d'homologie sans torsion. Cela correspond au fait que dans le polygone fondamental de la bouteille de Klein, une seule paire de côtés est collée en torsion, alors que dans le plan projectif, les deux côtés sont torsadés.
Un carré est un espace topologique contractable, ce qui implique une homologie triviale. Par conséquent, des coupes supplémentaires le déconnectent. Le carré n'est pas la seule forme dans le plan qui puisse être collée sur une surface. Le collage des côtés opposés d'un octogone, par exemple, produit une surface avec deux trous. En fait, toutes les surfaces fermées peuvent être produites en collant les côtés de certains polygones et tous les polygones à côtés égaux (2n-gones) peuvent être collés pour créer différentes variétés. Inversement, une surface fermée avec n classes non nulles peut être découpée en 2n-gone. Des variations sont également possibles, par exemple un hexagone peut également être collé pour former un tore[5].
La première théorie d'homologie reconnaissable a été publiée par Henri Poincaré dans son article fondateur "Analysis situs", J. Ecole polytech. (2) 1. 1-121 (1895). L'article introduit les classes et les relations d'homologie. Les configurations possibles des cycles orientables sont classées par les nombres de Betti de la variété (les nombres de Betti sont un raffinement de la caractéristique d'Euler). La classification des cycles non orientables nécessite des informations supplémentaires sur les coefficients de torsion[4].
La classification complète des 1- et 2-variétés est donnée dans le tableau.
| Variété | Caractéristique d'Euler χ |
Orientabilité | Nombres de Betti | Coefficient de torsion (1 dimension) | |||
|---|---|---|---|---|---|---|---|
| Symbole[5] | Nom | b0 | b1 | b2 | |||
| Cercle (1-variété) | 0 | Orientable | 1 | 1 | N / A | N / A | |
| Sphère | 2 | Orientable | 1 | 0 | 1 | aucun | |
| Tore | 0 | Orientable | 1 | 2 | 1 | aucun | |
| Plan projectif | 1 | Non-orientable | 1 | 0 | 0 | 2 | |
| Bouteille de Klein | 0 | Non-orientable | 1 | 1 | 0 | 2 | |
| Tore à 2 trous | −2 | Orientable | 1 | 4 | 1 | aucun | |
| Tore à g trous (genre = g) | 2 − 2g | Orientable | 1 | 2g | 1 | aucun | |
| Sphère avec c cross-caps | 2 − c | Non-orientable | 1 | c − 1 | 0 | 2 | |
| 2-variété avec g trous et c cross-caps (c > 0) | 2 − (2g + c) | Non-orientable | 1 | (2g + c) − 1 | 0 | 2 | |
- REMARQUES :
- Pour une surface non orientable, un trou équivaut à deux calottes croisées.
- Toute 2-variété est la somme connexe de g tore et c plans projectifs. Pour la sphère , g = c = 0.
Généralisation
Une variété avec une limite ou une variété ouverte est topologiquement distincte d'une variété fermée et peut être créée en effectuant une coupe dans toute variété fermée appropriée. Par exemple, le disque ou 1-balle est délimité par un cercle . Il peut être créé en coupant un cycle trivial dans n'importe quelle 2-variété et en gardant le morceau enlevé, en perçant la sphère et en étirant la ponction, ou en coupant le plan projectif. Cela peut aussi être vu comme remplir le cercle dans le plan.
Lorsque deux cycles peuvent être déformés de façon continue l'un par l'autre, la coupe le long de l'un d'eux produit la même forme que la coupe le long de l'autre, jusqu'à une certaine flexion et un certain étirement. Dans ce cas, les deux cycles sont dits homologues ou appartiennent à la même classe d'homologie. De plus, si un cycle peut être continuellement déformé en une combinaison d’autres cycles, alors couper le long du cycle initial est identique à couper le long de la combinaison des autres cycles. Par exemple, couper le long d'une figure 8 équivaut à couper le long de ses deux lobes. Dans ce cas, le chiffre 8 est dit homologue à la somme de ses lobes.
Deux variétés ouvertes ayant des limites similaires (jusqu’à certaines flexions et étirements) peuvent être collées ensemble pour former une nouvelle variété qui constitue leur somme liée.
Cette analyse géométrique des variétés n'est pas rigoureuse. À la recherche d'une plus grande rigueur, Poincaré développa l'homologie simpliciale d'une variété triangulée et créa ce que l'on appelle aujourd'hui un complexe en chaîne[7] - [8]. Ces complexes de chaîne (depuis très généralisés) forment la base de la plupart des traitements d'homologie modernes.
Dans de tels traitements, un cycle n'a pas besoin d'être continu: un cycle 0 est un ensemble de points, et couper le long de ce cycle correspond à la perforation de la variété. Un 1-cycle correspond à un ensemble de boucles fermées (une image de la 1-variété ) Sur une surface, couper le long d'un cycle donne des morceaux déconnectées ou une forme plus simple. Un 2-cycle correspond à une collection de surfaces incorporées telles qu'une sphère ou un tore, etc.
Emmy Noether et, indépendamment, Léopold Vietoris et Walther Mayer développèrent plus avant la théorie des groupes d'homologie algébrique de 1925 à 1928[9] - [10] - [11]. La nouvelle topologie combinatoire a formellement traité les classes topologiques en tant que groupes abéliens. Les groupes d'homologie sont des groupes abéliens finement générés, et les classes d'homologie en sont des éléments. Les nombres de Betti de la variété sont le rang de la partie libre du groupe d'homologie et les cycles non orientables sont décrits par la partie de torsion.
La propagation ultérieure de groupes d'homologie a entraîné un changement de terminologie et de point de vue, passant de "topologie combinatoire" à "topologie algébrique"[12]. L'homologie algébrique reste la méthode principale de classification des variétés[13].
Exemples informels
De manière informelle, l'homologie d'un espace topologique X est un ensemble d'invariants topologiques de X représentés par ses groupes d'homologie
où le -ième groupe d'homologie décrit les trous de dimension k dans X. Un trou à 0 dimension est simplement un espace entre deux composants, par conséquent décrit les composants de X reliés au chemin[14].

Une sphère unidimensionnelle est un cercle. Il possède un seul composant connecté et un trou unidimensionnel, mais aucun trou de dimension supérieure. Les groupes d'homologie correspondants sont donnés comme
où est le groupe d'entiers et est le groupe trivial. Le groupe représente un groupe abelien de type fini, avec un seul générateur représentant le trou unidimensionnel contenu dans un cercle[15].

Une sphère à deux dimensions a un seul composant connecté, pas de trous unidimensionnels, un trou bidimensionnel et pas de trous de dimensions supérieures. Les groupes d'homologie correspondants sont[15]
En général, pour une sphère à n dimensions Sn, les groupes d’homologie sont

Une boule à deux dimensions B2 est un disque solide. Il a une seule composante liée au trajet, mais contrairement au cercle, il n’a pas de trous unidimensionnels ou de trous de dimensions supérieures. Les groupes d'homologie correspondants sont tous triviaux à l'exception de . En général, pour une balle à n dimensions Bn[15],
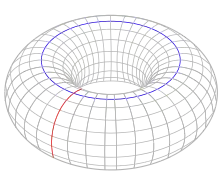
Le tore est défini comme un produit cartésien de deux cercles . Le tore a une composante liée à un chemin unique, deux trous unidimensionnels indépendants (indiqués par des cercles en rouge et bleu) et un trou bidimensionnel comme intérieur du tore. Les groupes d'homologie correspondants sont[16]
Les deux trous 1D indépendants forment des générateurs indépendants dans un groupe abélien de génération finie, exprimé par le groupe de produits cartésien. .
Construction de groupes d'homologie
La construction commence par un objet tel qu'un espace topologique X, sur lequel une première définit une chaîne complexe de C(X) codant des informations sur X. Un complexe de chaîne est une séquence de groupes abéliens ou de modules C0, C1, C2, ... reliés par des homomorphismes qui sont appelés opérateurs limite[16]. C'est,
où 0 désigne le groupe trivial et pour i < 0. Il est également nécessaire que la composition de deux opérateurs limite consécutifs soit triviale. C'est, pour tout n,
c'est-à-dire que l'application constante envoie chaque élément de Cn+1 à l'identité du groupe dans Cn−1. L'affirmation que la limite d'une limite est triviale est équivalente à , où désigne l'image de l'opérateur limite et son noyau. Les éléments de sont appelés limites et éléments de s'appellent des cycles.
Puisque chaque groupe de chaîne Cn est abélien, tous ses sous-groupes sont normaux. Puis parce que est un sous-groupe de Cn, est abélien, et , est donc un sous-groupe normal de . Ensuite, on peut créer le groupe quotient
appelé le n-ième groupe d'homologie de X. Les éléments de Hn(X) sont appelés classes d'homologie. Chaque classe d'homologie est une classe d'équivalence sur plusieurs cycles et deux cycles de la même classe d'homologie sont dits homologues[17].
Un complexe chaîne est exacte si l'image de la (n + 1)-ième application est toujours égale au noyau de la n-ième application. Les groupes d'homologie de X mesurent donc "à quel point" le complexe de chaîne associé à X est inexact[18].
Les groupes d'homologie réduits d'un complexe de chaîne C(X) sont définis comme des homologies du complexe de chaîne augmentée[19]
où l'opérateur limite est
pour une combinaison ∑ niσi de points σi, qui sont les générateurs fixes de C0. Les groupes d'homologie réduits coïncident avec pour i ≠ 0. L'extra dans le complexe de la chaîne représente l'application unique du simplexe vide à X.
Calcul du cycle et limite groupes est généralement assez difficile car ils ont un très grand nombre de générateurs. D'autre part, il existe des outils qui facilitent la tâche.
Les groupes d'homologie simpliciale Hn(X) d'un complexe simplicial X sont définis à l'aide du complexe de chaîne simplicial C(X), avec Cn(X) le groupe abélien libre généré par les n-simplexes de X. Les groupes d'homologie singulière Hn(X) sont définis pour tout espace topologique X et s'accordent avec les groupes d'homologie simpliciale pour un complexe simplicial.
Les groupes de cohomologie ressemblent formellement aux groupes d'homologie: on commence par un complexe différentiel, identique à un complexe de chaîne, mais dont les flèches, maintenant désignées par dn, vont dans le sens d'une augmentation de n plutôt que d'une diminution de n; alors les groupes de cocycles et des colimites découlent de la même description. Le n-ième groupe de cohomologie de X est alors le groupe quotient
par analogie avec le n-ième groupe d'homologie.
Types d'homologie
Les différents types de théorie de l'homologie découlent de l'application des foncteurs de différentes catégories d'objets mathématiques vers la catégorie des complexes en chaîne. Dans chaque cas, la composition du foncteur d’objets en complexes de chaînes et le foncteur de complexes de chaînes en groupes d’homologie définissent le foncteur d’homologie général de la théorie[20].
L'exemple motivant vient de la topologie algébrique : l'homologie simpliciale d'un complexe simplicial X. Ici, le groupe de chaînes Cn est le groupe ou module abélien libre dont les générateurs sont les simplexes de X orientés en n dimensions. L'orientation est capturée en ordonnant les sommets du complexe et en exprimant un simplexe orienté. comme un n-tuple de ses sommets listés par ordre croissant (ie dans l'ordre du sommet du complexe, où est le sommet apparaissant dans le tuple). L'application de Cn à Cn-1 est appelée l'application des limites et envoie le simplexe
à la somme formelle
qui est considéré comme 0 si n = 0. Ce comportement sur les générateurs induit un homomorphisme sur tout Cn comme suit. Étant donné un élément , écrivez-le comme la somme des générateurs , où X n est l’ensemble des n- complexes de X et les m i sont des coefficients de l’anneau C n est défini sur (généralement des entiers, sauf indication contraire). Puis définir
La dimension de la n-ième homologie de X s'avère être le nombre de "trous" dans X à la dimension n. Il peut être calculé en plaçant les représentations matricielles de ces applications de limites sous la forme normale de Smith.
Homologie singulière
En utilisant l'exemple d'homologie simpliciale comme modèle, on peut définir une homologie singulière pour tout espace topologique X. Un complexe de chaîne pour X est défini en prenant Cn comme groupe libre abélien (ou module libre) dont les générateurs sont tous des mappages continus de simplexes à n dimensions dans X. Les homomorphismes ∂n découlent des applications des limites des simplexes.
Homologie de groupe
En algèbre abstraite, on utilise l'homologie pour définir des foncteurs dérivés, par exemple les foncteurs de Tor. Ici, on commence avec un foncteur additif covariant F et un module X. Le complexe de chaîne pour X est défini comme suit: on recherche d'abord un module libre F1 et un homomorphisme surjectif p1 : F1 → X. On trouve alors un module libre F2 et un homomorphisme surjectif p2 : F2 → ker(p1). En continuant ainsi, une séquence de modules libres Fn et d'homomorphismes pn peut être définie. En appliquant le foncteur F à cette séquence, on obtient un complexe en chaîne; l'homologie Hn de ce complexe ne dépend que de F et X et est, par définition, le n-ième foncteur dérivé de F appliqué à X.
Un usage courant de (co)homologie de groupe est de classer les groupes d'extension possibles E qui contiennent un G-module M donné en tant que sous-groupe normal et qui ont un groupe de quotient donné G, de sorte que G = E/M.
Autres théories d'homologie
- Borel–Moore homology
- Cellular homology
- Cyclic homology
- Hochschild homology
- Floer homology
- Intersection homology
- K-homology
- Khovanov homology
- Morse homology
- Persistent homology
- Steenrod homology
Foncteurs d'homologie
Des complexes de chaînes forment une catégorie: un morphisme de la chaîne complexe (Dn: An → A n-1) à la chaîne complexe (en: Bn → B n-1) est une séquence d'homomorphismes fn: An → Bn tels que pour tout n. La n-ième homologie Hn peut être vue comme un foncteur covariant de la catégorie des complexes de chaînes à la catégorie des groupes (ou modules) abéliens.
Si le complexe de la chaîne dépend de l'objet X de manière covariante (signifiant que tout morphisme X → Y induit un morphisme du complexe de la chaîne de X au complexe de la chaîne de Y ), alors Hn sont des foncteurs covariants de la catégorie X appartient à la catégorie des groupes (ou modules) abéliens.
La seule différence entre l'homologie et la cohomologie est que, en cohomologie, les complexes de chaîne dépendent de manière contravariante de X et que, par conséquent, les groupes d'homologie (appelés groupes de cohomologie dans ce contexte et notés Hn) forment des foncteurs contravariants de la catégorie X appartient à la catégorie des groupes ou modules abéliens.
Propriétés
Si (dn: An → An-1) est une chaîne complexe telle que tous sauf un nombre fini de An sont nuls, et les autres sont des groupes abélien finiment engendrés (ou des espaces vectoriels de dimension finie), on peut alors définir la caractéristique d'Euler
(en utilisant le rang dans le cas des groupes abéliens et la dimension Hamel dans le cas des espaces vectoriels). Il s'avère que la caractéristique d'Euler peut également être calculée sur le niveau d'homologie :
et, en particulier dans la topologie algébrique, cela fournit deux façons de calculer l'important invariant χ pour l'objet X qui a donné lieu au complexe de la chaîne.
Chaque suite exacte
de complexes en chaîne donne lieu à une longue suite exacte de groupes d'homologie
Toutes les applications de cette longue séquence exacte sont induites par les applications entre les complexes en chaîne, à l'exception des applications Hn(C) → Hn -1(A). Ces dernières sont appelées homomorphismes de connexion et sont fournies par le lemme de zig-zag. Ce lemme peut être appliqué à l'homologie de nombreuses façons qui aident au calcul de groupes d'homologie, telles que les théories de l'homologie relative et les séquences de Mayer-Vietoris.
Applications
Application en mathématiques pures
Les théorèmes notables prouvés en utilisant l'homologie sont les suivants:
- Le théorème du point fixe de Brouwer : Si f est une application continue de la boule Bn sur elle-même, alors il existe un point fixe a ∈ Bn avec f(a) = a.
- Invariance du domaine : Si U est un sous-ensemble ouvert de Rn et f : U → Rn est une application continue injective, alors V = f (U) est ouvert et f est un homéomorphisme entre U et V.
- Le théorème de la boule chevelue : tout champ de vecteurs sur la 2-sphère (ou plus généralement, la 2k-sphère pour tout k ≥ 1) disparaît à un moment donné.
- Le théorème de Borsuk–Ulam : toute fonction continue d'une n-sphère dans le n-espace euclidien place une paire de points antipodaux sur le même point. (Deux points d’une sphère sont appelés antipodaux s’ils se trouvent dans des directions exactement opposées à partir du centre de la sphère.)
- Invariance de la dimension : si les sous-ensembles ouverts non vides et sont homéomorphes, alors .[21]
Application en sciences et ingénierie
Dans l'analyse des données topologiques, les jeux de données sont considérés comme un échantillon de nuages de points d'une variété multiple ou algébrique intégrée dans l'espace euclidien. En reliant les points voisins les plus proches dans le nuage en une triangulation, une approximation simpliciale de la variété est créée et son homologie simpliciale peut être calculée. Trouver des techniques permettant de calculer de manière fiable l'homologie à l'aide de diverses stratégies de triangulation sur plusieurs échelles de longueur est le sujet de l'homologie persistante[22].
Dans les réseaux de capteurs, les capteurs peuvent communiquer des informations via un réseau ad-hoc qui change de manière dynamique dans le temps. Pour comprendre le contexte global de cet ensemble de mesures locales et de voies de communication, il est utile de calculer l'homologie de la topologie du réseau pour évaluer, par exemple, les trous dans la couverture[23].
Dans la théorie des systèmes dynamiques en physique, Poincaré a été l’un des premiers à examiner l’interaction entre la variété invariante d’un système dynamique et ses invariants topologiques. La théorie de Morse relie la dynamique d'un écoulement de gradient sur une variété à, par exemple, son homologie. L'homologie de Floer s'étend à des variétés infiniment dimensionnelles. Le théorème KAM a établi que des orbites périodiques peuvent suivre des trajectoires complexes ; en particulier, ils peuvent former des tresses qui peuvent être étudiées en utilisant l'homologie de Floer[24].
Dans une classe de méthodes par éléments finis, il peut être nécessaire de résoudre les problèmes de valeurs limites pour les équations différentielles impliquant l'opérateur de Hodge-Laplace sur des domaines topologiquement non triviaux, par exemple dans les simulations électromagnétiques. Dans ces simulations, la solution est facilitée en fixant la classe de cohomologie de la solution en fonction des conditions aux limites choisies et de l'homologie du domaine. Les domaines FEM peuvent être triangulés, à partir desquels l'homologie simpliciale peut être calculée[25] - [26].
Logiciel
Divers logiciels ont été développés pour calculer des groupes d'homologie de complexes de cellules finies. Linbox est une bibliothèque C++ permettant d'effectuer des opérations matricielles rapides, y compris la forme normale de Smith ; il s'interface avec Gap et Maple. Chomp, CAPD::Redhom et Perseus sont également écrits en C++. Tous les trois implémentent des algorithmes de prétraitement basés sur l'équivalence simple-homotopie et la théorie de Morse discrète afin de réaliser des réductions préservant l'homologie des complexes de cellules en entrée avant de recourir à l'algèbre matricielle. Kenzo est écrit en Lisp et, en plus de l'homologie, il peut également être utilisé pour générer des présentations de groupes d'homotopie de complexes simpliciaux finis. Gmsh inclut un résolveur d'homologie pour les maillages d'éléments finis, qui peut générer des bases de cohomologie directement utilisables par un logiciel d'éléments finis[25].
Voir également
- Nombre de Betti
- Espace cycle
- Axiomes d'Eilenberg–Steenrod
- Théorie de l'homologie extraordinaire
- Algèbre homologique
- Conjectures homologiques en algèbre commutative
- Dimension homologique
- Théorème de Künneth
- Liste des théories de la cohomologie - contient également une liste des théories d'homologie
- Cohomologie de De Rham
Remarques
- du grec ὁμός homos "identique"
- Stillwell 1993, p. 170
- Weibel 1999, p. 2–3 (dans le PDF)
- Richeson 2008 p.254.
- Weeks, J.R.; The Shape of Space, CRC Press, 2002.
- Richeson (2008)
- Richeson 2008 p.258
- Weibel 1999, p. 4
- Hilton 1988, p. 284
- Par exemple L'émergence de la notion de groupe d'homologie, Nicolas Basbois (PDF), nomme explicitement Noether comme étant l'inventeur des homologies.
- Hirzebruch, Friedrich, Emmy Noether and Topology dans Teicher 1999, p. 61–63.
- Topologie algébrique par John McCleary (PDF)
- Richeson 2008 p.264.
- Spanier 1966, p. 155
- Gowers 2010, p. 390–391
- Hatcher 2002, p. 106
- Hatcher 2002, p. 105–106
- Hatcher 2002, p. 113
- Hatcher 2002, p. 110
- Spanier 1966, p. 156
- Hatcher 2002, p. 126.
- « CompTop overview » (consulté le )
- « Robert Ghrist: applied topology » (consulté le )
- van den Berg, Ghrist, Vandervorst et Wójcik, « Braid Floer homology », Journal of Differential Equations, vol. 259, no 5, , p. 1663–1721 (DOI 10.1016/j.jde.2015.03.022, lire en ligne)
- Pellikka, S. Suuriniemi, L. Kettunen et C. Geuzaine, « Homology and Cohomology Computation in Finite Element Modeling », SIAM J. Sci. Comput., vol. 35, no 5, , B1195–B1214 (DOI 10.1137/130906556, lire en ligne)
- Arnold, Richard S. Falk et Ragnar Winther, « Finite element exterior calculus, homological techniques, and applications », Acta Numerica, vol. 15, , p. 1–155 (DOI 10.1017/S0962492906210018)
Références
- Cartan, Henri Paul et Eilenberg, Samuel (1956) Homological Algebra Princeton University Press, Princeton, NJ, OCLC 529171
- Eilenberg, Samuel et Moore, J. C. (1965) Foundations of relative homological algebra (Memoirs of the American Mathematical Society number 55) American Mathematical Society, Providence, R.I., OCLC 1361982
- Hatcher, A., (2002) Algebraic Topology Cambridge University Press, (ISBN 0-521-79540-0). Detailed discussion of homology theories for simplicial complexes and manifolds, singular homology, etc.
- Homology group à Encyclopaedia of Mathematics
- Hilton, Peter (1988), "A Brief, Subjective History of Homology and Homotopy Theory in This Century", Mathematics Magazine, Mathematical Association of America, 60 (5): 282–291, JSTOR 2689545
- Teicher, M., ed. (1999), The Heritage of Emmy Noether, Israel Mathematical Conference Proceedings, Bar-Ilan University/American Mathematical Society/Oxford University Press, (ISBN 978-0-19-851045-1), OCLC 223099225
- "Homology (Topological space)". PlanetMath.
- Richeson, D.; Euler's Gem: The Polyhedron Formula and the Birth of Topology, Princeton University (2008)
- Spanier, Edwin H. (1966). Algebraic Topology, Springer, p. 155,. (ISBN 0-387-90646-0).
- Timothy Gowers, June Barrow-Green, Imre Leader (2010), The Princeton Companion to Mathematics, Princeton University Press, (ISBN 9781400830398).
- John Stillwell (1993), Classical Topology and Combinatorial Group Theory, Springer, doi:10.1007/978-1-4612-4372-4_6, (ISBN 978-0-387-97970-0).
- Charles A. Weibel (1999), History of Homological Algebra, chapter 28 in the book History of Topology by I.M. James, Elsevier, (ISBN 9780080534077).






































![{\displaystyle [\emptyset ]\longrightarrow X}](https://img.franco.wiki/i/6ce21624866825d0c90e1d5a93ddd41cc74d43fa.svg)






![{\displaystyle (\sigma [0],\sigma [1],\dots ,\sigma [n])}](https://img.franco.wiki/i/9893cb6a42a8658098e94b07b7b017fcbf48b942.svg)
![{\displaystyle \sigma [0]<\sigma [1]<\cdots <\sigma [n]}](https://img.franco.wiki/i/9eeaa6286bd46a6c0ab76d0920a115a03216aa57.svg)
![{\displaystyle \sigma [i]}](https://img.franco.wiki/i/48f6feb944eb1c860bd78391bccee81f01f4bd93.svg)


![{\displaystyle \sigma =(\sigma [0],\sigma [1],\dots ,\sigma [n])}](https://img.franco.wiki/i/7145641dc88fcdeaf628fe229c7a6d5c5857ac57.svg)
![{\displaystyle \partial _{n}(\sigma )=\sum _{i=0}^{n}(-1)^{i}\left(\sigma [0],\dots ,\sigma [i-1],\sigma [i+1],\dots ,\sigma [n]\right),}](https://img.franco.wiki/i/1adc96f7f6d2efdd0ba4e7ed003441ebd6e3d32f.svg)











