Théorie de Morse

Le tore posé verticalement et les lignes de niveau de la fonction hauteur.

Une des illustrations les plus simples des idées générales de la théorie de Morse est la « reconstruction » d'un tore à partir de la fonction hauteur. Soit donc un tore M (surface ayant la forme d'une chambre à air), posé verticalement. Soit h l'application qui à un point du tore associe sa coordonnée dans la direction verticale (la hauteur).

Pour des valeurs de z de plus en plus grandes on procède à la description de la partie de la surface qui est de hauteur inférieure à z. Cette partie est appelée le sous-niveau de hauteur z :

${\displaystyle M^{z}=\{x\in M,h(x)\leq z\}.}$

Point selle.

Dans cette description, quatre points particuliers vont jouer un rôle. Ils portent le nom de points critiques pour la fonction hauteur. Ce sont les points de hauteur minimale et maximale d'une part, et deux autres points qualifiés de « point-selle » ou « point col » d'autre part. L'aspect du tore à la proximité du point selle le plus bas est donné par la figure ci-contre. Il se caractérise par la présence de directions montantes et descendantes lui donnant effectivement la forme d'un col.

• Pour z strictement inférieur à la hauteur du minimum, le sous-niveau M^z est vide.
• Pour z légèrement supérieur à cette valeur, le sous-niveau prend la forme d'une calotte.
• Lorsque z augmente, le sous-niveau ne change pas de nature topologique jusqu'à atteindre la hauteur du premier point selle.
• Dépasser légèrement la hauteur du premier point selle modifie le sous-niveau, qui devient cylindre. À homotopie près cette modification revient à ajouter une « anse » à la calotte précédente.
• De nouveau le type topologique ne change pas quand l'altitude est modifiée, jusqu'au deuxième point selle.
• Encore une fois, franchir le point selle modifie le type topologique, et revient à ajouter une nouvelle anse au cylindre (on obtient un tore percé).
• Atteindre la hauteur maximum permet de finir la figure en rajoutant un disque pour fermer le tore.

La règle qui semble se dégager est que lorsque l'altitude z varie, la topologie du sous-niveau M^z reste inchangée tant que z évolue entre deux valeurs critiques. Le franchissement d'un niveau critique engendre une modification de la topologie par ajout d'un élément (point, droite, disque…) qui dépend directement de la nature du point critique. Cette règle doit en fait être amendée pour tenir compte de deux phénomènes « exceptionnels » :

• il se peut que plusieurs points critiques soient situés à la même altitude ;
• la modification de topologie ne se décrit simplement que pour les points critiques non dégénérés.

Les lignes de gradient sont un outil adapté à la comparaison des sous-niveaux entre eux. Dans le cas de la "fonction hauteur" donnée en exemple, il s'agirait des lignes de plus grande pente tracées sur le tore. Pour les définir en général, il faut munir la variété d'une métrique riemannienne. Il est alors possible d'introduire le champ de vecteurs gradient ∇f de la fonction f. Les lignes de gradient de f sont les courbes intégrales de ce champ de vecteurs, c'est-à-dire les solutions de l'équation différentielle :

${\displaystyle {\dot {x}}(t)=\nabla f\left[x(t)\right].}$

Les lignes de gradient sont orthogonales aux hypersurfaces de niveau, définies par l'équation f = constante. Sur une variété riemannienne compacte sans bord (M, g), le champ de gradient est globalement intégrable, c'est-à-dire que toutes les lignes de gradient sont définies sur tout ℝ.

Passage d'un point critique d'indice 1.

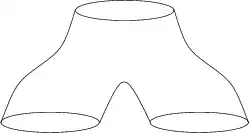
Les sous-niveaux M^z de la fonction f sont définis comme précédemment. Les deux théorèmes suivants permettent de comparer les sous-niveaux entre eux.

Théorème : description des zones sans point critique

Si a < b, et si f⁻¹([a, b]) est compact sans point critique, alors M^a et M^b sont des variétés à bord difféomorphes.

Plus précisément, la partie ajoutée à M^a pour obtenir M^b, qui ressemble à une jambe de pantalon, peut être décrite en suivant les lignes de gradient de la fonction f. Cette partie est difféomorphe au produit [a, b]×f⁻¹({a}) et, toujours en suivant ces lignes de gradient, M^b se rétracte par déformation sur M^a.

Théorème : passage d'un point critique

Soit p un point critique non dégénéré de f d'indice d' et q = f(p) la valeur critique correspondante. On suppose que a < q < b et que f⁻¹([a, b]) est compact. On suppose enfin que p est le seul point critique correspondant à la valeur q. Alors, pour ε assez petit, M^q+ε est homotopiquement équivalent à M^q-ε auquel on ajoute une d-cellule.

Quelques lignes de gradient de la fonction hauteur qui est une fonction de Morse (pour un tore penché). On a tracé toutes les courbes exceptionnelles, car toutes les autres vont directement du minimum vers le maximum.

Une fonction de Morse f est une fonction de classe C² à valeurs réelles dont tous les points critiques sont non dégénérés. Selon un résultat de René Thom[1], si la variété M est compacte sans bord, les fonctions de Morse constituent un ouvert dense de l'espace de Fréchet C^k(M, ℝ) des fonctions de classe C^k sur M, et ce pour toute classe de régularité k ≥ 2. Le résultat s'étend partiellement aux variétés compactes avec bord avec les précautions qui s'imposent. Autrement dit, une fonction générique est de Morse.

Sur une variété riemannienne compacte sans bord (M, g), les lignes de gradient admettent des limites en ±∞, limites qui sont des points critiques distincts de f. Sous une hypothèse de généricité pouvant porter sur f ou sur g, leurs indices sont décroissants. On dit alors que les lignes du gradient de f vont d'un point critique à un autre par indice décroissant. En chaque point critique a d'indice k, on peut distinguer les lignes qui aboutissent à ce point critique, et celles qui en sont issues. La réunion des premières forme une sous-variété de M, difféomorphe à ℝ^k, appelée variété stable du point a. Ainsi la variété M apparaît comme la réunion des variétés stables de ses différents points critiques, ce qui en donne une décomposition en k-cellules pour différentes valeurs de k.

La variété instable en a est définie de même comme réunion des lignes de gradient originaires de a. Toujours pour un point d'indice k, elle est difféomorphe à ℝ^n–k.

• Homologie de Floer
• Théorie de Morse discrète (en)
• Analyse globale
• Théorie de Picard-Lefschetz

• François Laudenbach, Transversalité, Courants et Théorie de Morse - Un cours de topologie différentielle, Éditions de l'École polytechnique, 2011
• (en) John Milnor, Morse Theory, Princeton University Press, 1963 (ISBN 0-691-08008-9)
• (en) Yukio Matsumoto, An Introduction to Morse Theory, 2002
• (en) Marston Morse, The Calculus of Variations in the Large, AMS, coll. « Colloquium Publications » (n^o 18), New York, 1934