Histoire du mètre
L'histoire du mètre, unité de longueur, trouve son origine à la Renaissance en Europe. Le mètre est officiellement défini en France à la Révolution française ; sa définition évolue et s'affine ensuite dans les siècles suivants.
Les premiers étalons de longueur connus remontent à l'âge du bronze. La métrologie connaît un tournant majeur avec la révolution scientifique qui débute avec les travaux de Nicolas Copernic en 1543. Des mesures de plus en plus précises sont nécessaires et les scientifiques cherchent à s'affranchir des étalons métalliques dont la longueur varie avec la température. Afin de faciliter leurs calculs, ils préfèrent également le système décimal aux différents systèmes complexes de subdivision en usage à l'époque. Au XVIIe siècle, de nombreux scientifiques envisagent la longueur du pendule battant la seconde comme étalon de longueur. Le mot mètre est né de cette première définition et vient de l'italien « metro cattolico » signifiant en français « mesure universelle ». Cette définition est abandonnée lorsqu'il apparaît que la longueur du pendule change avec la pesanteur qui varie en fonction de la latitude du lieu en raison de la rotation de la Terre sur elle-même. De plus, il s'avère que l'étude des variations de la longueur du pendule constitue un moyen complémentaire aux mesures d'arcs méridiens pour déterminer la figure de la Terre.
Avec la Révolution française de 1789 s'affirme le désir d'unifier les mesures et de s'affranchir de l'héritage de l'Ancien Régime. Le mètre est adopté et sa définition affinée comme étant la dix-millionième partie de la méridienne passant par Paris et reliant le pôle Nord à l'Équateur. Cette distance est extrapolée à partir de la mesure de l'arc de méridien reliant Dunkerque à Barcelone sur la base d'un aplatissement de 1/334. Le mètre est conservé à Paris sous la forme d'un étalon de platine, le Mètre des Archives. En 1889, il est remplacé à l'initiative de l'Association géodésique internationale par trente prototypes internationaux distribués à travers le monde. La comparaison de ces étalons de platine iridié entre eux et avec le Mètre des Archives implique le développement d'instruments de mesure spéciaux et la définition d'une échelle de température reproductible.
Les progrès de la science permettent finalement de dématérialiser l'étalon du mètre. Ainsi en 1960, une nouvelle définition basée sur un multiple de la longueur d'onde de la radiation émise lors de la transition entre deux niveaux de l'atome de krypton 86 permet de rendre l'étalon du mètre universellement disponible par des mesures de laboratoire. Cette définition est mise à jour en 1983 en se basant sur une longueur spécifiée en termes de vitesse de la lumière et est reformulée en 2019 : « Le mètre, symbole m, est l'unité de longueur du SI. Il est défini en prenant la valeur numérique fixée de la vitesse de la lumière dans le vide, c, égale à 299 792 458 lorsqu'elle est exprimée en m s−1, la seconde étant définie en fonction de ΔνCs. »
Histoire de la définition
| Base de définition | Date | Incertitude absolue |
Incertitude relative |
|---|---|---|---|
| 1⁄10000000 d'une moitié de méridien (quart de la circonférence de la Terre), mesuré par Delambre et Méchain | 1798 | 0,5–0,1 mm | 10−4 |
| Premier prototype du Mètre des Archives, une barre de platine servant d'étalon | 1799 | 0,05–0,01 mm | 10−5 |
| Barre de platine iridié au point de fusion de la glace (1re CGPM) | 1889 | 0,2–0,1 µm | 10−7 |
| Barre de platine iridié au point de fusion de la glace, sous pression atmosphérique, soutenue par deux rouleaux (7e CGPM) | 1927 | n.a. | n.a. |
| 1 650 763,73 longueurs d'onde de la lumière d'une transition spécifique de l’isotope 86 du krypton (11e CGPM) | 1960 | 0,01–0,005 µm | 10−8 |
| Longueur de la distance parcourue par la lumière dans le vide en 1⁄299792458 de seconde (17e CGPM) | 1983 | 0,1 nm | 10−10 |
Premières unités de longueur
.jpg.webp)
La coudée de Nippur est l'une des plus anciennes unités de longueur connue. Comme son nom l'indique, avant l'invention du mètre pendant la Révolution française, beaucoup d'unités de longueur étaient basées sur des parties du corps humain. Le plus ancien étalon de longueur en métal connu correspond à cette unité sumérienne et date de 2650 ans avant notre ère. Il s'agit d'une barre de cuivre découverte à Nippur, sur les rives de l'Euphrate, qui est conservée au musée archéologique d'Istanbul[2] - [3] - [4].
Les archéologues considèrent que cette unité longue de 51,85 cm est à l'origine du pied romain. En effet, les Égyptiens divisent la coudée sumérienne en 28 doigts et 16 de ces doigts donnent un pied romain de 29,633 cm[2] - [4].
Les Romains imposent les unités de mesures romaines dans tout leur empire. Jusqu'à Charlemagne, le système romain des poids et mesures est à peu près le seul usité dans les royaumes francs. Le pied romain est divisé en 4 palmes, en 12 pouces ou en 16 doigts. Une coudée romaine équivaut à 1,5 pied, un double pas à 5 pieds. Un mile contient 1 000 doubles pas ou 5 000 pieds. Une lieue romaine comprend 7 500 pieds romains[5] - [6].
Au cours du Moyen Âge, de nouveaux pieds de différentes longueurs font leur apparition en Europe. Ils dérivent tous plus ou moins directement du pied romain. Ces pieds sont divisés en 12 pouces, eux-mêmes divisés en 12 lignes de 6 points chacune. Des multiples de ces pieds deviennent les étalons de longueur dans différentes villes d'Europe. Ainsi la toise de Paris comprend 6 pieds de roi et la verge anglaise (le yard) mesure 3 pieds de Londres. Quand les Allemands n'expriment point la sorte de pied dont ils se servent, il faut l'entendre du pied rhinlandique. Le palme en usage à Rome est divisé en 12 onces, et l'once en 5 minutes ; ce qui fait 60 minutes au palme. Dix palmes font la canne, qu'on nomme d'architecte[2] - [7] - [8].
En France, la perche ordinaire varie suivant les différentes provinces ou les différentes coutumes ; c'est à celui qui va faire des arpentages dans un pays d'en prendre connaissance chez le juge du lieu : à Paris, la perche contient trois toises, soit 18 pieds ; pour les travaux royaux, elle a 22 pieds. Ainsi, la perche carrée, mesure de Paris, est un carré qui a trois toises de long sur trois de large. L'arpent contient 100 perches carrées, c'est-à-dire, en le considérant comme un carré, qu'il contient 10 perches de longueur sur 10 perches de largeur. L'acre en Angleterre et en Normandie est de 160 perches carrées[9] - [10] - [11].
Les mesures de longueur en Hollande, Flandres, Suède et une partie de l'Allemagne sont l'aune, mais une aune différente dans tous ces pays. L'aune est un bâton d'une certaine longueur qui sert à mesurer les étoffes, les toiles, les rubans. En Angleterre, la mesure de longueur qui sert de règle dans le commerce est la verge (yard) qui contient trois pieds de Londres, ou 7/9 de l'aune de Paris ; de sorte que neuf yard font sept aunes de Paris. La varre est une mesure dont on se sert en Espagne, particulièrement dans le royaume d'Aragon, pour mesurer les tissus. Sa longueur est semblable à celle de la canne de Toulouse. Trois aunes de Paris font deux varres d'Espagne. L'aune de France a beaucoup de rapport à la verge d'Angleterre et de Séville ; à la canne de Provence, de Toulouse, de Naples, de Gênes, de Livourne et autre villes d'Italie ; à la varre d'Aragon ; à la barre de Castille et de Valence ; à la brasse de Lucques, Venise, Boulogne ; au palme de Sicile ; au pic de Constantinople, de Smyrne et du Caire ; à la gueze des Indes et à celle de Perse[12] - [8] - [5] - [13].
Dans presque toute l'Italie, à Bologne, Modène, Venise, Florence, Lucques, Milan, Bergame, Mantoue, c'est la brasse qui est en usage, mais qui est de différentes longueurs dans chacune de ces villes. La mesure de longueur des Portugais est le cavedos et le varas. La mesure longue du Piémont et de Turin est le raz[8].
Les Moscovites ont deux mesures de longueur, l'arcin et la coudée. Les Turcs et les Lévantins ont le pied. Le cobre est la mesure des étoffes en Chine. En Perse et dans quelques États des Indes, on se sert de la guèze, dont il y a deux sortes, la guèze royale et la petite guèze. Le royaume de Pégu et quelques autres lieux des Indes se servent du cando, qui est égal à l'aune de Venise ; mais le cando de Goa est une longue mesure qui revient à 17 aunes de Hollande. La mesure longue des Siamois est le ken[8].
Mesure universelle
Avec l'augmentation de l’activité scientifique, au XVIIe siècle, semble apparaître la possibilité d'une « mesure universelle » (selon l'expression du Britannique John Wilkins[14]) ou d'un « metro cattolico » (selon celle de l'Italien Tito Livio Burattini[15]), d'où vient le mot actuel mètre, basés sur un phénomène naturel plutôt que sur un décret royal et utilisant le système décimal plutôt que l'une des autres bases de subdivisions, souvent duodécimales, qui coexistent à l'époque.
Cette grandeur naturelle est d'abord le temps. La Royal Society envisage, dès 1660, la longueur d'un pendule battant la seconde selon une proposition de Christian Huygens et Ole Christensen Rømer qui suivent une idée déjà formulée en 1644 par Marin Mersenne. C'est là le début du mètre avec son ordre de grandeur actuel. En effet, l'idée de baser une unité de longueur universelle sur une grandeur tirée de la nature a été proposée bien avant qu'elle n'obtienne un succès définitif avec l'adoption de la figure de la Terre et de la méridienne de Delambre et Méchain en 1799. La longueur du pendule à seconde, un pendule qui oscille avec un battement d'une seconde, soit une période de deux secondes, est de loin la proposition qui a obtenu le plus de suffrages. Toutefois, Christian Huygens démontre, en 1673, l'effet de la force centrifuge qui explique l'augmentation de la longueur du pendule avec la latitude[16] - [17] - [18].

Le principe de la décimalisation est également proposé par Gabriel Mouton, qui formule le projet parallèle de définir l'unité de longueur selon la longueur d'une minute d'arc de méridien afin de la rapporter à une grandeur géométrique[19]. En 1669, Jean Picard mesure un arc de méridien au moyen de triangulations géodésiques et préfigure ainsi la mesure de la Méridienne de France[13] - [17] - [18].
Reprenant l'idée de Christopher Wren[14], Wilkins, Mouton et Picard envisagent la longueur d'un pendule simple (un pendule de demi-période égale à une seconde) comme moyen de dématérialiser l'étalon de longueur : de tels pendules, décrits peu auparavant par Christiaan Huygens, ont une longueur proche du mètre moderne (ainsi que d'autres mesures d'usage à l'époque comme le yard)[13] - [19]. Après la réfection de la toise du Châtelet, Jean Picard, supposant que la pesanteur est partout identique, propose une mesure universelle dont il détermine le rapport avec la toise de Paris. Il définit le rayon astronomique comme la longueur du pendule battant la seconde à Paris. Il appelle le double de cette mesure la toise universelle, qui correspond à 881 lignes de la toise de Paris[20] - [19]. Cependant, il s'avère rapidement que la longueur d'un pendule simple battant la seconde varie selon le lieu : l'astronome français Jean Richer mesure une différence de 0,3 % de la longueur du pendule entre Cayenne (en Guyane française) et Paris[21].
« La toise dont nous venons de parler, et que nous avons choisie comme la mesure la plus certaine, et la plus usitée en France, est celle du grand Châtelet de Paris, suivant l'original qui en a été récemment rétabli. Elle est de 6 pieds ; le pied contient 12 pouces, et le pouce 12 lignes : mais de peur qu'il n'arrive à notre toise, comme à toutes les mesures anciennes, dont il ne reste plus que le nom, nous l'attacherons à un original, lequel étant tiré de la nature même, doit être invariable et universel. [...] S'il se trouvait par expérience que les pendules fussent de différente longueur en différents lieux, la supposition que nous avons faite touchant la mesure universelle tirée des pendules ne pourrait subsister ; mais cela n'empêcherait pas que dans chaque lieu il n'y eût une mesure perpétuelle et invariable. La longueur de la toise de Paris et celle du pendule à secondes, telle que nous l'avons établie, seront soigneusement conservées dans le magnifique observatoire que Sa Majesté fait bâtir pour l'avancement de l'astronomie. »
— Picard, Jean, Mesure de la Terre, 1671, Paris, Imprimerie royale
En 1780, Alexis-Jean-Pierre Paucton publie Métrologie ou Traité des mesures, poids et monnoies des anciens peuples & des modernes. Il rapporte plusieurs valeurs de la longueur du pendule battant la seconde mesurées par différents astronomes et scientifiques à plusieurs endroits du globe. Les résultats varient en fonction de la résistance de l'air, des marées et de la dilatation des matériaux du pendule et instruments de mesures due aux changements de température. Ces variables affectent les mesures et s'ajoutent aux variations locales de la pesanteur, ce qui nuit à la recherche d'universalisme ainsi qu'à la stabilité nécessaire dans la conception d'un étalon dématérialisé[22].
Le mètre lié à la figure de la Terre

Lors de la fondation de l'Académie des sciences sous le règne de Louis XIV, les proportions du système solaire sont connues grâce aux lois de Kepler. Les astronomes français, sous la direction de Jean-Dominique Cassini, font une première détermination de la distance de la Terre au Soleil en 1672. Le rayon de la Terre constitue la base de tous les calculs. Jean Picard mesure un arc de méridien dans la région de Paris et rapporte la distance mesurée à la différence des latitudes des deux extrémités de sa méridienne pour calculer la circonférence de la Terre et son diamètre[Note 1]. C'est le commencement de la mesure de la Méridienne de France. Elle sera prolongée, puis mesurée à nouveau plusieurs fois au cours de l'histoire de la géodésie. La Terre est alors considérée comme une sphère[23] - [24] - [18] - [17] - [20].
Toutefois, Jean Richer, lors de son séjour en Guyane, constate que le pendule battant la seconde est plus court à Cayenne qu'à Paris. Christian Huygens et Isaac Newton expliquent cette différence de longueur du pendule par l'effet de la force centrifuge due à la rotation de la Terre sur elle-même (dont l'effet diminue avec la latitude) s'opposant à l'action de la gravitation et en déduisent que la Terre doit être aplatie aux pôles. Cela donne lieu à une formidable polémique entre les cartésiens tenant d'une Terre allongée aux pôles et les newtoniens tenant d'un aplatissement. De plus, cette nouvelle donnée remet en question la valeur du rayon terrestre telle que Jean Picard l'avait calculée. Dès lors, la détermination de la figure de la Terre revêt, en plus de sa signification pour la cartographie, une importance primordiale en astronomie dans la mesure où le diamètre de la Terre est l'unité à laquelle toutes les distances célestes doivent être rapportées[25] - [26] - [27] - [20] - [17].
Des expéditions géodésiques sont conduites au début du XVIIIe siècle en Laponie et au vice-royaume du Pérou et apportent la preuve de la forme ellipsoïde de la Terre. En 1766, la règle géodésique employée pour l'expédition franco-espagnole en Équateur, la toise du Pérou est adoptée comme étalon de la toise sous le nom de toise de l'Académie[17] - [18] - [28].
Dans son célèbre ouvrage « Théorie de la Figure de la Terre, Tirée des Principes de l'Hydrostatique » publié en 1743, Alexis Claude Clairaut (1713–1765) fait une synthèse des rapports existant entre la pesanteur et la forme de la Terre. Clairaut y expose son théorème qui établit une relation entre la pesanteur mesurée à différentes latitudes et l'aplatissement de la Terre considérée comme un sphéroïde composé de couches concentriques de densités variables. Vers la fin du XVIIIe siècle, les géodésiens cherchent à concilier les valeurs de l'aplatissement tirées des mesures d'arcs méridiens avec celui que donne le sphéroïde de Clairaut tiré de la mesure de la pesanteur. En 1789, Pierre-Simon de Laplace obtient, par un calcul prenant en compte les mesures d'arcs méridiens connues à l'époque, un aplatissement de 1/279. La gravimétrie lui donne un aplatissement de 1/359. Adrien-Marie Legendre, quant à lui, trouve à la même époque un aplatissement de 1/305. La Commission des Poids et Mesures adoptera, en 1799, un aplatissement de 1/334 en combinant l'arc du Pérou et les données de la méridienne de Delambre et Méchain.

Durant la Révolution française, la triangulation de Delambre et Méchain détermine le rapport entre la toise et le mètre. Ce dernier est défini comme la 10 000 000e partie du quart du méridien terrestre[Note 2] - [Note 3], mesuré en toises de Paris. La distance du pôle Nord à l'équateur terrestre est extrapolée à partir de l'arc de méridien compris entre Dunkerque et Barcelone. Le point fondamental de la méridienne de Delambre et Méchain est le Panthéon[18] - [29].
On croit pouvoir attaquer la base du système métrique en signalant quelques erreurs qui paraissent s'être glissée dans les mesures des deux savants français. Méchain s'était même aperçu d'une inexactitude qu'il n'osa malheureusement pas avouer. En effet, l'imprécision des instruments de mesure et des méthodes de calcul est alors telle que, dans l'intervalle de seulement quelques années, des relevés plus fiables auraient donné des résultats différents. Cela n'invalide le mètre en aucune façon, mais illustre seulement que les progrès scientifiques permettront de meilleures déterminations de la figure de la Terre. En 1866, lors de la conférence de l'Association géodésique internationale à Neuchâtel, Carlos Ibáñez e Ibáñez de Ibero annonce le concours de l'Espagne à la mesure de la Méridienne de France. En 1870, François Perrier est chargé de reprendre la triangulation entre Dunkerque et Barcelone. La combinaison des travaux géodésiques effectués au Royaume-Uni, en France, en Espagne et en Algérie permet de mesurer un grand arc méridien de 27° qui s'étend des îles Shetland, par 61° de latitude aux confins du Sahara, par 34°[30] - [31] - [32] - [33] - [34] - [29] - [17] - [35].
Au cours du XIXe siècle, le mètre est progressivement adopté en Europe continentale et en Amérique, notamment pour un usage scientifique, et est officiellement établi comme unité de mesure internationale par la Convention du Mètre de 1875. En effet, la géodésie est une des premières disciplines scientifiques à fonder une association internationale à une époque où les étalons de longueur les plus importants sont des règles géodésiques. En 1889, le Système international d'unité repose sur trois unités de base : le kilogramme, la seconde et le mètre[Note 4]. Ce dernier est choisi par l'Association géodésique internationale en 1867, année de l'adhésion de l'Espagne qui est le premier pays européen à adopter le mètre comme unité géodésique après les États-Unis d'Amérique[36] - [37] - [38] - [39] - [40] - [32].
Les prototypes internationaux du mètre resteront en vigueur jusqu'en 1960. Les progrès de la métrologie[Note 5] et une meilleure prise en compte de la dilatation thermique des étalons métalliques permettent l'avènement d'une nouvelle ère de la géodésie avec le développement de l'étude de la figure de la Terre au moyen de la détermination de la pesanteur par le pendule et de l'utilisation du théorème de Clairaut[41] - [42] - [43] - [44].
Actuellement, la définition du mètre est liée à la vitesse de la lumière qui équivaut à 299 792 458 m/s. Les relations entre la métrologie et la géodésie sont encore d'actualité dans la mesure où la réalisation pratique du mètre est rendue possible en tout lieu grâce aux horloges atomiques embarquées dans les satellites GPS[45].
La toise, unité géodésique internationale

La révolution copernicienne (XVIe au XVIIIe siècle) correspond au passage d'une cosmographie géocentrique à un modèle héliocentrique et à la découverte de la loi universelle de la gravitation. Durant cette période, avec la création de l'Académie royale des sciences de Paris en 1666, la géodésie se développe sous l'impulsion des astronomes français avec le double objectif d'établir la carte de France et de déterminer la taille et la forme de la Terre (la figure de la Terre). Ces dernières données sont, à l'époque, nécessaires au calcul de la distance de la Terre au Soleil, distance qui est à l'origine de l'unité astronomique dont la valeur actuelle est de 149 597 870 700 mètres. En 1672, profitant du passage de Mars à proximité de la Terre, Jean Richer à Cayenne, Jean-Dominique Cassini et Jean Picard à Paris observent la parallaxe de Mars et font une première mesure de la distance de la Terre au Soleil. Selon leurs observations et leurs calculs (basés sur les lois de Kepler), la distance de la Terre au Soleil est de 23 000 rayons terrestres. Ainsi, jusqu'à l'invention de nouvelles méthodes de mesure des distances séparant les astres, la détermination de la figure de la Terre revêt une importance primordiale en astronomie, dans la mesure où le diamètre de la Terre est l'unité à laquelle toutes les distances célestes doivent être rapportées[17] - [46] - [24] - [47] - [48] - [23].
Taille de la Terre et gravitation universelle

En 250 av. J.-C., Ératosthène est le premier à préciser les principes selon lesquels la taille de la Terre peut être déterminée. Cette méthode sera utilisée jusqu'au XXe siècle. Elle consiste à comparer une ligne mesurée sur la surface de la Terre avec l'arc astronomique correspondant. Ératosthène observe que le Soleil est à la verticale de Syène en Égypte, le jour du solstice d'été, alors qu'à Alexandrie, au même moment, la distance zénithale du Soleil est de 7° 12′ ou 1/50 de la circonférence d'un cercle. Supposant que les deux villes sont situées sur le même méridien et estimant la distance qui les sépare à 5 000 stades, il en déduit que la circonférence de la Terre équivaut à 250 000 stades[17].
Posidonios adapte la méthode d'Ératosthène en comparant la hauteur de l'étoile Canopus (plutôt que celle du Soleil) pour mesurer l'arc astronomique entre Alexandrie et Rhodes[17].
En 1617, Willebord Snellius invente le principe de la triangulation géodésique et mesure avec un quadrant une chaîne de triangles de 55 100 toises de long correspondant à un arc de 1 degré d'amplitude entre Alkmaar et Berg-op-Zoom en s'appuyant sur une base mesurée près de Leyde aux Pays-Bas. Il exprime la longueur de sa méridienne en toises[17] - [18].
La toise se divise en 6 pieds, le pied en 12 pouces, le pouce en 12 lignes et la ligne en 12 points[49]. Une toise correspond donc à 864 lignes. La base des unités de longueur à Paris est, à l'époque, le pied du roi. Depuis 1394, l'étalon qui définit le pied du roi est la toise. Elle comprend six pieds et est exposée sur un pilier du Châtelet. Cet étalon a fait l'objet d'une réfection en 1668-1670. Selon certains auteurs, la longueur du pied aurait varié de 1,757 mm au cours de la restauration de l'étalon. L'ancien pied du roi correspondrait à 326,596 mm avant 1668 et à 324,839 mm après 1668. D'autres auteurs considèrent que de nombreuses inconnues physiques ont marqué la vie des étalons en fer sur lesquelles ont porté ces mesures à l'époque et voient dans le pied du roi une unité stable depuis le XIIIe siècle[50].

En 1669, Jean Picard améliore le procédé de Snellius en adaptant des lunettes astronomiques au quart de cercle mobile qu'il utilise pour la mesure de sa méridienne[17]. Il mesure 57 060 toises pour un degré d'arc de méridien et en déduit un diamètre de 6 538 594 toises (soit un rayon d'environ 6 365,6 kilomètres) pour une Terre supposée sphérique[18] - [20]. Picard exprime la circonférence de la Terre en toises de Paris, Newton reprend cette mesure exprimée en pieds de Paris dans ses "Principes mathématiques de la philosophie naturelle" (20 541 600 toises de Paris correspondant à 123 249 600 pieds de Paris)[18] - [20] - [51].
La mesure de Picard a probablement servi à confirmer la théorie de la gravitation universelle[18]. Tout d'abord, Galilée remarque que les corps tombent à la surface de la Terre avec une accélération uniforme (g). Kepler calcule ensuite que les carrés des périodes (T) des orbites des planètes sont proportionnels aux cubes des distances moyennes (R) entre les planètes et le Soleil pour chaque planète du système solaire :
Newton déduit de la définition de l'accélération centripète (a) et de la loi des périodes de Kepler que l'accélération centripète (a), subie par un objet en orbite, est proportionnelle à l'inverse du carré du rayon moyen (R) de l'orbite en question :
,
,
d'où
,
,
d'où
,
soit
Les données dont Newton dispose indiquent, en outre, que le rayon de la Terre équivaut à 1/60 de la distance séparant le centre de la Terre de celui de la Lune. Considérant que la force gravitationnelle exercée par la Terre sur la Lune est inversement proportionnelle au carré de la distance qui les sépare, Newton conclut que l'accélération centripète (a) à laquelle la Lune est soumise correspond au 1/3600 de l'accélération (g) qui s'exerce à la surface de la Terre :
Par ailleurs, l'accélération centripète (a) exercée par la Terre sur la Lune peut aussi être calculée à partir de la période orbitale de la Lune (T = 27,33 jours) et de la distance Terre-Lune (R = 60 fois le rayon de la Terre) selon la formule :
Les deux calculs donnent un résultat concordant :
Ce qui confirme que l'accélération centripète qui maintient la Lune dans son orbite autour de la Terre est bien la même que celle qui régit la chute des corps à la surface de la Terre[52].
Forme de la Terre et gravitation universelle
.jpg.webp)
La fin du XVIIe siècle voit naître une controverse scientifique concernant la figure de la Terre opposant les cartésiens, tenants d'une Terre allongée aux pôles, et les newtoniens, tenants d'un modèle ellipsoïdal de la Terre. Ces derniers affirment, conformément aux théories de Newton et Huygens, qu'en raison de la rotation de la Terre sur elle-même, celle-ci doit être un ellipsoïde aplati. La mesure du méridien de Paris dirigée par Jean-Dominique Cassini, puis Jacques Cassini, montre au contraire que les degrés du méridien de Paris diminuent du sud au nord. Ce qui constitue un argument en faveur d'une Terre allongée aux pôles. À l'inverse, les observations de Saturne et Jupiter montrent l’aplatissement de ces planètes. De plus, la diminution de la longueur du pendule battant la seconde, observée par Jean Richer à Cayenne, est expliquée, selon Newton, par une diminution de la pesanteur, corrélée à un renflement de la Terre à l'équateur et provoquée par la rotation de la Terre sur elle-même. L'Académie des sciences envoie deux missions pour mesurer des arcs de méridiens en Laponie et en Équateur pour trancher la question. Deux règles géodésiques sont construites pour ces expéditions, la toise du Nord et la toise du Pérou. Leur longueur est ajustée sur la toise du Châtelet, fixée depuis 1668 à l'extérieur du Grand Châtelet. Les résultats de ces deux missions et la révision du Méridien de Paris confirment que la Terre est aplatie aux pôles[53] - [18] - [28].
Depuis 1766, l'étalon de la toise, principale unité de longueur en vigueur en France, est la toise de l'Académie. Cet étalon, également appelé toise du Pérou ,est la règle géodésique utilisée lors de l'expédition organisée par l'Académie des sciences avec le concours de l'Espagne au vice-royaume du Pérou (actuel Équateur) entre 1735 et 1744. Il servira à définir la longueur du mètre qui correspond à 3 pieds et 11,296 lignes de la toise de l'Académie (soit la fraction 0,513 074 de sa longueur : 5 130 740 toises correspondant à 10 000 000 mètres)[18] - [28]. En effet, le , la Constituante adopte le projet de l'Académie des sciences définissant le mètre comme la dix-millionième partie de la moitié de méridien terrestre (ou d'un quart de grand cercle passant par les pôles), ou encore le dix-millionième de la distance pour aller par le plus court chemin d’un pôle à l’équateur mesurée en toises de Paris[54] - [30] - [Note 3].
Pour la mesure du Méridien de Paris entre Dunkerque et Barcelone (1792-1798), Jean-Charles de Borda conçoit un instrument de mesure des bases géodésiques constitué de quatre règles de deux toises de longueur. Les comparaisons effectuées à l'époque montrent que la règle no 1 de Borda mesure exactement le double de la toise du Pérou et que les quatre règles mises bout à bout forment une longueur égale à huit fois la toise du Pérou à la température de 12,5° (degré centigrade). Chaque règle de platine de 12 pieds de longueur est recouverte d'une autre règle de cuivre mesurant 11 pieds, 6 pouces de longueur fixée à une extrémité de la règle de platine. Ce dispositif permet de comparer la dilatation relative des deux règles et sert de thermomètre métallique[55].
Essor de la géodésie dans l'Empire britannique et en Europe continentale
Les triangulations géodésiques débutent en Grande-Bretagne avec la jonction des observatoires de Greenwich et Paris en 1787, quatre ans après la publication de la Description géométrique de la France par César-François Cassini[56] - [57]. Dans la seconde moitié du XIXe siècle, l'unité anglaise officielle (le yard ou verge anglaise,divisé en trois pieds, alors que la toise est divisée en six pieds) est employée comme unité géodésique au Royaume-Uni, en Inde, en Australie et dans la colonie du Cap. Selon une comparaison des standards géodésiques effectuée par Alexander Ross Clarke à l'Ordnance Survey, une toise correspond à 1 949,036 32 millimètres et un yard à 914,391 80 millimètres. La longueur actuelle du yard correspond à 0,914 4 mètre. Il est divisé en trois pieds de 30,48 centimètres. En effet, depuis 1959, le yard est défini en relation avec le système métrique[37] - [38] - [58] - [13].
« Le XIXe siècle verra l'essor pratique de la géodésie en même temps que son approfondissement théorique. Clairaut, d'Alembert, Euler avaient en Lagrange, Laplace, Legendre, Gauss les successeurs de haute classe capables de faire faire d'immenses progrès aux mathématiques pures, mais aussi de s’intéresser aux problèmes débouchant directement sur des applications pratiques. La mécanique céleste, la théorie du potentiel (en particulier les développements du potentiel newtonien), les méthodes de calcul numérique, etc., dont le développement intéresse tant l'astronomie et la géodésie, leur sont redevables de progrès décisifs dont l'impact se fait plus que jamais ressentir actuellement.
Si la géodésie s'internationalise, ses méthodes restent fondamentalement celles du XVIIIe siècle (triangulation, astronomie de position, mesure de la pesanteur, mesures de temps correspondantes), mais la précision des instruments, la rigueur des méthodes de travail seront poussées jusqu'aux limites extrêmes.
La mesure de la méridienne par Delambre et Méchain, de Dunkerque à Barcelone, base du système métrique, donne le coup d'envoi. Elle aboutit aux définitions suivantes :
- Ellipsoïde de la Commission des Poids et Mesures ;
- Quart du méridien[Note 2], 10 000 000 m (par définition) ;
- Aplatissement, 1/334 ;
- 1 mètre = 443,296 lignes de la toise de l'Académie ;
- 1 toise = 1,949 036 6 m.
De nombreux pays poussent activement leurs triangulations, échangent des renseignements, comparent leurs résultats.
En 1835, Morse, aux États-Unis, invente la télégraphie qui va donner aux géodésiens la possibilité de mesurer avec une précision inconnue jusqu'alors les longitudes astronomiques, et de les comparer avec les longitudes calculées sur l'ellipsoïde.
Kater, Bessel, Defforges un peu plus tard, mesurent avec soin la pesanteur absolue. De grandes triangulations sont observées : arc de Struve d'Hammerfest au delta du Danube, triangulation de l'Inde (Everest), triangulations nationales (Angleterre, Empire autrichien, États allemands, Espagne, France, Algérie, Italie). […]
L'Association internationale de Géodésie, en gestation depuis 1867, sera créée en 1885. Elle se prononce pour l'adoption du système métrique, appuie la création d'un Bureau International des Poids et Mesures, organise un Service international des Latitudes, fait reprendre au Spitzberg et en Amérique du Sud des mesures d'arcs de méridien. »
— Levallois, Jean-Jacques, La Vie des sciences, mai 1986
Au XIXe siècle, la toise est l'unité géodésique la plus utilisée en Europe. Deux copies de la toise du Pérou sont notamment effectuées à Paris par Fortin, la première en 1821 pour Friedrich Georg Wilhelm von Struve et la seconde en 1823 pour Friedrich Wilhelm Bessel. En 1862, lors de la fondation de l'Association pour la mesure des degrés en Europe centrale par Johann Jacob Baeyer, l'étalon géodésique prussien (la toise de Bessel) sera choisi par l'association comme étalon géodésique international[37] - [59] - [60].
Friedrich Georg Wilhelm von Struve, dont l’ellipsoïde est adopté par Carlos Ibáñez e Ibáñez de Ibero pour la carte de l'Espagne, donne son nom au grand arc géodésique qui s'étend de la mer Glaciale à la mer Noire. L'arc géodésique de Struve tire son origine du besoin des puissances européennes, après le congrès de Vienne en 1815, d'établir des frontières et des cartes militaires plus précises. Selon cette approche, le tsar Alexandre Ier de Russie charge l'astronome Friedrich Georg Wilhelm von Struve de réaliser la mesure d'un arc géodésique qui sera inscrit en 2005 au patrimoine mondial de l'UNESCO[61].
Bessel met en application dans le domaine des observations géodésiques la méthode des moindres carrés, découverte simultanément par Legendre et Gauss. Bessel est également à l'origine des investigations effectuées au XIXe siècle sur la figure de la Terre au moyen de la détermination de l'intensité de la gravitation par le pendule et de l'utilisation du théorème de Clairaut. Les études qu'il conduit de 1825 à 1828 et sa détermination de la longueur du pendule simple battant la seconde à Berlin sept ans plus tard marquent le début d'une nouvelle ère de la géodésie[17] - [44].
Parallèlement au rôle qu'elle jouera dans le processus d'internationalisation du mètre, l'Association géodésique poursuivra son développement pour devenir une des premières associations scientifiques d'envergure mondiale[60] - [36] - [62]. Durant cette période, Adolphe Hirsch en sera le secrétaire perpétuel, Carlos Ibáñez e Ibáñez de Ibero le président, tandis que Friedrich Robert Helmert succédera à Johann Jacob Baeyer à la direction du Bureau central de l'association[63] - [32] - [64].
Définition méridionale

Peu de progrès effectifs sont accomplis en vue de l'établissement d'une « mesure universelle » avant la Révolution française de 1789. La France est particulièrement touchée par la prolifération de mesures de longueur et le besoin de réforme est largement admis par tous les partis politiques, quitte à utiliser la Révolution pour y parvenir. Talleyrand revient à l'idée du pendule devant l'Assemblée constituante le 8 mai 1790, suggérant que la mesure soit prise à la latitude 45° N (qui passe entre Grenoble et Bordeaux) ; malgré le soutien de l'Assemblée, la Grande-Bretagne ayant décliné l'invitation d'établir une base commune de mesure, la proposition de Talleyrand ne sera pas suivie[19] - [5] - [Note 6] - [65] - [66]. Le même jour, un décret concernant la monnaie est adopté. Il dispose que l'Académie des sciences se prononcera sur l'échelle de division "qu'elle croira la plus convenable, tant pour le poids que pour les autres mesures et pour les monnaies"[19].
.jpg.webp)
La question de la réforme des mesures est confiée à l'Académie des sciences, qui désigne une commission présidée par Jean-Charles de Borda. Borda est un fervent défenseur de la décimalisation : il est l'inventeur du cercle répétiteur, un instrument de mesure permettant une grande précision de mesure des angles entre deux points, et il insiste pour qu'il soit étalonné en degrés et en grades (1⁄100 de quart de cercle), avec 100 minutes dans un grade et 100 secondes dans une minute[62] - [67]. Borda considère que le pendule battant la seconde est un mauvais choix pour un étalon car la seconde (comme unité de temps) n'est pas une unité du système décimal de la mesure du temps - un système fixant 10 heures par jour, 100 minutes par heure et 100 secondes par minute - introduit en 1793. En revanche, le mètre découle aussi bien du degré que du grade, en ce sens que si 10 000 kilomètres correspondent à 100 grades d'arc de méridien (le grade étant la centième partie de l'angle droit), alors le mètre correspond à la dix-millionième partie de la moitié[Note 2] de la longueur du méridien terrestre (soit un arc de méridien de 90 degrés ou de 100 grades).
La commission – qui compte parmi ses membres Lagrange, Laplace, Monge et Condorcet – décide que la nouvelle unité de longueur sera égale au dix-millionième de la distance du pôle Nord à l’équateur (le quadrant de la circonférence de la Terre), extrapolée à partir de la Méridienne de France (l'arc de méridien mesuré sur le trajet du méridien de Paris entre Dunkerque et Barcelone), plutôt qu'à la longueur du pendule battant la seconde[5]. En effet, les triangulations géodésiques sont utilisées, depuis le XVIIe siècle, pour déterminer les dimensions de la Terre. Elles donnent lieu à plusieurs méridiennes fondamentales visant à étayer différentes hypothèses concernant la figure de la Terre, qui constitue un problème de la plus haute importance en astronomie dans la mesure où le diamètre de la Terre est l'unité à laquelle toutes les distances célestes doivent être rapportées[17]. En plus d'un accès facile pour les géodésiens français, le choix du méridien de Paris est aussi judicieux pour des raisons scientifiques : les deux extrémités de la portion du quadrant allant de Dunkerque à Barcelone (environ 1 000 km, soit un dixième du total) sont situées au niveau de la mer ; de plus, ce tronçon se situe près du milieu du quadrant, où les effets de l’aplatissement de la Terre sont supposés être les plus importants[5]. Enfin, le cercle répétiteur, conçu par Borda et utilisé par les Français lors de la jonction des observatoires de Greenwich et Paris en 1787, fait espérer que cette nouvelle mesure de la Méridienne de France atteindra une précision proche de la perfection[56].

La mesure de la méridienne est confiée à Pierre Méchain et Jean-Baptiste Delambre. Elle s'étend sur plus de six ans (1792–1798). Les difficultés techniques ne sont pas les seuls problèmes rencontrés par les scientifiques pendant cette période houleuse qui suit la Révolution française : Méchain et Delambre, puis Arago, sont retenus en détention à plusieurs reprises au cours de leurs relevés, et Méchain meurt en 1804 de la fièvre jaune, contractée au cours de sa tentative d'amélioration de ses premières mesures au nord de l’Espagne. Dans un premier temps, la commission calcule une valeur provisoire du mètre équivalant à 443,44 lignes en se fondant sur des relevés antérieurs[Note 7]. Cette valeur est officialisée le [68].
Le projet est divisé en deux parties – une section nord de 742,7 km, reliant le beffroi de Dunkerque à la cathédrale de Rodez, menée par Delambre, et une section sud de 333,0 km de Rodez au château de Montjuïc à Barcelone, assurée par Méchain[69] - [Note 8]. Delambre mesure une base d'environ 10 km (6 075,90 toises) de longueur le long d'une ligne droite entre Melun et Lieusaint. Dans une opération qui lui prend six semaines, il mesure précisément la base avec quatre règles de platine de deux toises de longueur (précisément 3,898 073 2 mètres)[69] - [38]. Il utilise par la suite, quand cela est possible, les points, utilisés par Cassini lors de sa triangulation de la France en 1744. La base de la section sud, de longueur similaire (6 006,25 toises), correspond également au tronçon rectiligne d'une route située entre Vernet (près de Perpignan) et Salces (aujourd'hui Salses-le-Château)[70]. Bien que la partie de Méchain soit moitié moindre que celle de Delambre, elle nécessite la traversée des Pyrénées et comprend des parties non mesurées de l'Espagne. Après la jonction, des deux géodésiens, une commission internationale, composée de Gabriel Císcar, Jean-Baptiste Delambre, Pierre-Simon Laplace, Adrien-Marie Legendre, Pierre Méchain, Jean Henri van Swinden et Johann Georg Tralles, fait les calculs pour la longueur du quart de méridien sur la base d'un aplatissement de la Terre de 1/334 obtenu en combinant les résultats de la méridienne avec ceux de la mission du Pérou, et trouve 5 130 740 toises[19]. Comme le mètre est, par définition, équivalent à la dix-millionième partie de cette distance, il correspond à 0,513 074 toises de Paris ou 3 pieds et 11,296 lignes de la toise de l'Académie[28] - [18]. Ce résultat est adopté par le Corps législatif le 4 messidor an VII (22 juin 1799)[5].
Mètre des Archives

Pendant que Méchain et Delambre effectuent leurs relevés, la commission commande une série de barres de platine basées sur le mètre provisoire. Quand le résultat final est connu, la barre dont la longueur est la plus proche de la définition méridionale du mètre est retenue et placée dans les Archives nationales le (4 messidor de l’an VII dans le calendrier républicain) comme enregistrement permanent du résultat[5]. Ce mètre-étalon sera dorénavant dénommé mètre des Archives.
Le système métrique, le système d'unités basé sur le mètre, est officiellement adopté en France le (19 frimaire de l’an VIII[71]) et devient l'unique système de poids et mesures dès 1801[68]. A la Restauration en 1815, les anciens noms des unités de longueur sont repris, mais la toise est redéfinie comme mesurant exactement deux mètres : c'est le système des mesures usuelles, qui perdure jusqu'en 1840, lorsque le système décimal redevient le seul autorisé[5]. La République helvétique adopte le système métrique en 1803, peu avant son effondrement. Les Pays-Bas adoptent le mètre à partir de 1816, premier pays à établir durablement le système métrique[28].
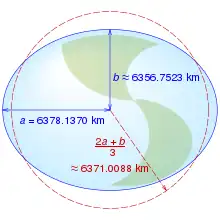
Avec l'extension de la Méridienne de France, il apparaît rapidement que le résultat de Méchain et Delambre (443,295 936 lignes pour un mètre)[Note 7], sur la base de la définition méridionale du mètre, est un peu trop court. En effet, tandis que l'Ordnance Survey prolonge la méridienne au Royaume-Uni jusqu'aux îles Shetland, Arago et Biot étendent la triangulation en Espagne jusqu'à l'île de Formentera ,dans l'ouest de la mer Méditerranée, entre 1806 et 1809, et trouvent qu'un dix-millionième du quadrant de la Terre est équivalent à 443,31 lignes : une triangulation ultérieure augmente la valeur à 443,39 lignes[5] - [72]. La valeur moderne, selon le sphéroïde de référence WGS 84, est de 1,000 196 57 × 107 m pour la distance du pôle à l'équateur[Note 9].
Louis Puissant déclare, dès 1836, devant l'Académie des sciences que Delambre et Méchain ont commis une erreur dans la mesure de la méridienne de France[73]. Toutefois, le mètre des Archives reste l'étalon légal et usuel en France, bien qu'il ne corresponde pas exactement à la définition méridionale. Lorsqu'il est décidé (en 1867) de créer un nouveau mètre-étalon international, la longueur choisie est celle du mètre des Archives « dans l'état dans lequel il sera trouvé »[74] - [42].
L’étude de la Terre précède la physique et contribuera à l’élaboration de ses méthodes. Celle-ci n’est d’abord qu’une philosophie naturelle dont l’objet est l’étude de phénomènes naturels comme le champ magnétique terrestre, la foudre et la pesanteur[36].
En 1832, Carl Friedrich Gauss étudie le champ magnétique terrestre et propose d’ajouter la seconde aux unités fondamentales que sont le mètre et le kilogramme sous la forme du système CGS (centimètre, gramme, seconde). En 1836, il fonde en collaboration avec Alexander von Humboldt et Wilhelm Edouard Weber le Magnetischer Verein, la première association scientifique internationale. En effet, la coordination de l’observation des phénomènes géophysiques dans différents points du globe revêt une importance primordiale et est à l’origine de la création des premières associations scientifiques internationales[75] - [36].
La fondation du Magnetischer Verein est suivie par celle de l’Association géodésique pour la mesure des degrés en Europe centrale à l’initiative de Johann Jacob Baeyer. Friedrich Wilhelm Bessel est à l’origine des investigations effectuées au XIXe siècle sur la figure de la Terre au moyen de la détermination de la pesanteur par le pendule et de l’utilisation du théorème de Clairaut. Les études qu’il conduit de 1825 à 1828 et sa détermination de la longueur du pendule battant la seconde à Berlin sept ans plus tard marquent le début d’une nouvelle ère de la géodésie[36] - [44].

En effet, le pendule réversible tel qu'il est utilisé par les géodésiens à la fin du XIXe siècle est en grande partie dû aux travaux de Bessel, car ni Johann Gottlieb Friedrich von Bohnenberger, son inventeur, ni Kater, qui l'utilise dès 1818, ne lui apportent les perfectionnements qui résulteront des précieuses indications de Bessel et qui le convertiront en l'un des plus admirables instruments qu'il sera donné aux scientifiques du XIXe siècle d'employer[44].
Le pendule réversible construit par les frères Repsold est utilisé en Suisse dès 1865 par Émile Plantamour pour la mesure de la pesanteur dans six stations du réseau géodésique helvétique. Suivant l'exemple donné par ce pays et sous le patronage de l'Association géodésique internationale, l'Autriche, la Bavière, la Prusse, la Russie et la Saxe entreprennent des déterminations de la pesanteur sur leurs territoires respectifs[44].
Toutefois, ces résultats ne pourront être considérés que comme provisoires dans la mesure où ils ne prennent pas en compte les mouvements que les oscillations du pendule impriment à son plan de suspension, qui constituent un important facteur d'erreur de mesure de la durée des oscillations et de la longueur du pendule[44].
En effet, la détermination de la gravité par le pendule est soumise à deux types d'erreur. D'une part la résistance de l'air et d'autre part les mouvements que les oscillations du pendule impriment à son plan de suspension. Ces mouvements sont particulièrement importants avec l'appareil conçu par les frères Repsold sur les indications de Bessel, car le pendule a une importante masse afin de contrecarrer l'effet de la viscosité de l'air. Alors qu’Émile Plantamour effectue une série d'expériences avec cet appareil, Adolphe Hirsch trouve le moyen de mettre en évidence les mouvements du plan de suspension du pendule par un ingénieux procédé d'amplification optique. Isaac-Charles Élisée Cellérier, un mathématicien genevois, et Charles Sanders Peirce mettront indépendamment au point une formule de correction qui permettra d'utiliser les observations faites au moyen de ce type de gravimètre[76] - [44].
Le prototype international du mètre constituera la base du nouveau système international d'unités, mais il n'aura plus aucune relation avec les dimensions de la Terre que les géodésiens s'efforcent de déterminer au XIXe siècle. Il ne sera plus que la représentation matérielle de l'unité du système. Si la métrologie de précision a profité des progrès de la géodésie, celle-ci ne peut continuer à prospérer sans le concours de la métrologie. En effet, toutes les mesures d'arcs terrestres et toutes les déterminations de la pesanteur par le pendule doivent impérativement être exprimées dans une unité commune. La métrologie se doit donc de créer une unité adoptée et respectée par toutes les nations de façon à pouvoir comparer avec la plus grande précision toutes les règles ainsi que tous les battants des pendules employés par les géodésiens. Ceci de manière à pouvoir combiner les travaux effectués dans les différentes nations afin de mesurer la Terre[44].
Le mètre et l'United States Coast Survey (lever topographique côtier des États-Unis)

En 1805, Ferdinand Rudolph Hassler, géodésien suisse, arrive aux États-Unis avec dans ses bagages des copies du « mètre des Archives » et du « kilogramme des Archives ». À cette époque, l'expansion du trafic maritime commercial sur les côtes américaines rend nécessaire la création de cartes côtières précises. Une loi promulguant la création de l'United States Coast Survey est votée par le Congrès des États-Unis et approuvée par le président Thomas Jefferson, le 10 février 1807. L'exécution de la loi est confiée au département du Trésor dont le secrétaire est Albert Gallatin. Ce dernier met au concours le poste de directeur de ce qui deviendra la première agence scientifique civile du gouvernement des États-Unis[77] - [78].
Le projet de Ferdinand Rudolph Hassler est accepté avec l'aval de la Société américaine de philosophie. Il consiste à mesurer des triangles de trente miles (soit 48,280 3 kilomètres) de côté le long du littoral en déterminant les azimuts des côtés de ces triangles et la longitude et la latitude de leurs sommets. Puis, dans un second temps, il s'agit de mesurer de plus petits triangles (dont la longueur des côtés serait d'une dizaine de miles, soit environ 16 kilomètres) à l'intérieur des premiers afin de déterminer de manière détaillée un grand nombre de points pouvant être reportés précisément sur la carte. Hassler projette de déterminer la taille des triangles en mesurant plusieurs bases à l'aide de règles géodésiques de sa conception, qui figurent probablement parmi les éléments les plus originaux des instruments rassemblés pour cette entreprise. En effet, alors que la plupart des règles géodésiques utilisées à cette époque en Europe sont étalonnées sur la toise, Hassler décide d'utiliser une règle étalonnée sur le mètre. Par ailleurs, Hassler met au point un système de lecture au microscope qui lui permet de juxtaposer, sans contact les différents éléments de son appareil de mesure des bases[77] - [78] - [37].
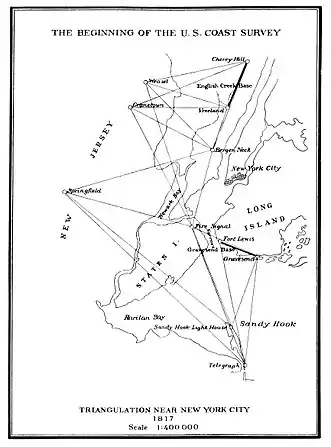
En 1811, Hassler se rend en Angleterre pour y faire construire les instruments géodésiques nécessaires à son projet. Depuis, l'Angleterre, il se rend à plusieurs reprises à Paris pour des missions diplomatiques pour le compte des États-Unis. Durant son séjour en Europe, la guerre anglo-américaine est déclarée et le matériel scientifique destiné aux relevés topographiques est séquestré par le gouvernement britannique. Hassler devra attendre jusqu'en 1815 pour revenir aux États-Unis avec ses instruments[77] - [78].
Hassler est nommé Superintendant of the Coast Survey (directeur du service des levers côtiers) en 1816. Avant de commencer sa campagne géodésique, il fait construire un chariot pour transporter son matériel. Il commence son travail au printemps 1817. Après seulement quelques mois de campagne, le Congrès lui retire sa charge et décide, par mesure d'économie, de confier le lever côtier à l'armée américaine, qui s'avérera incapable de faire substantiellement avancer ce travail au cours des quatorze années suivantes[77] - [78].
À l'époque, les unités de mesure aux États-Unis ne sont pas unifiées et il existe de grandes divergences entre les différents États qui portent préjudice aux échanges commerciaux. En 1830, le Congrès des États-Unis décide d'agir et Hassler est chargé par le président Jackson de produire des étalons à distribuer aux différents États. Hassler propose l'introduction du système métrique, mais le Congrès opte pour le British Parliamentary Standard de 1758 comme unité de longueur et pour le Troy Pound of Great Britain de 1824 comme unité de poids. En effet, le système métrique ne sera rendu international qu'en 1875 par la Convention du Mètre. En Europe comme aux États-Unis, l'uniformisation des unités de mesures sera confiée à des géodésiens[77] - [78].
En 1832, Hassler réalise les étalons de longueur, de poids et de capacité pour le département du Trésor. Quatre ans plus tard, le Congrès des États-Unis ordonne que ces étalons soient distribués à chaque État de l'Union, afin d'uniformiser les poids et mesures. Cela constitue une étape d'une importance cruciale dans la constitution de l'infrastructure technologique qui, en se développant, donnera naissance au National Institute of Standards and Technology[77] - [78].
À l'âge de 62 ans, Hassler est à nouveau nommé Superintendant of the Coast Survey, le 9 août 1832. En 1834, il mesure à Fire Island, au sud de Long Island, une base géodésique au moyen de son appareil de mesure des bases constitué de quatre barres de fer de deux mètres de longueur juxtaposées. Toutes les mesures du relevé côtier des États-Unis seront rapportées au mètre[77] - [78] - [38].
Lors de la Conférence générale des poids et mesures de 1889, le délégué américain exprimera l'espoir qu'après avoir été adopté par les géodésiens, le mètre soit rapidement adopté par la population américaine dans son ensemble[79] - [80].
Le mètre et l'arc de méridien d'Europe-Afrique de l'Ouest
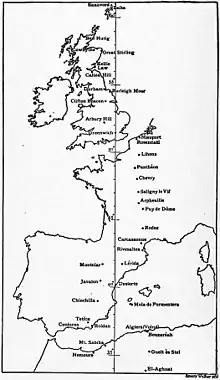
François Arago et Jean-Baptiste Biot publient, en 1821, un quatrième volume complétant l'œuvre de Delambre et Méchain dans lequel ils déterminent la variation de la pesanteur et des degrés terrestres sur le prolongement du Méridien de Paris allant jusqu'aux îles Baléares au sud et aux îles Shetland au nord. Dans l'introduction de cet ouvrage, Arago projette le prolongement du Méridien de Paris jusqu'en Algérie par la triangulation géodésique de l'Espagne et de l'Algérie, puis par leur jonction par-dessus la Méditerranée[72] - [Note 10] - [Note 11].
En 1853, le gouvernement espagnol décide de la mise en œuvre d'une grande carte topographique de l'Espagne. Carlos Ibáñez e Ibáñez de Ibero et Carlos Saavedra Menesès sont désignés pour en effectuer les travaux préparatoires. En effet, tout l'outillage scientifique et technique nécessaire à cette entreprise est à créer. L'Espagne ayant adopté le système métrique en 1849, Carlos Ibáñez e Ibáñez de Ibero se rend à Paris avec Carlos Saavedra Menesès pour faire construire par Brunner une règle à traits, calibrée sur le mètre, afin de mesurer la base géodésique centrale d'Espagne[81]. Des répliques de la règle bimétallique conçue pour l'Espagne seront construites pour la France, l'Égypte et l'Allemagne. L'appareil Ibáñez, un second instrument de mesure des bases muni de thermomètres, est construit à Paris par les fils Brunner afin de simplifier et d'accélérer les mesures. Il est utilisé pour les mesures des huit bases espagnoles effectuées de 1865 à 1879, puis pour celles des trois bases suisses en 1880-1881. À l'époque, la mesure d'une base de 2400 mètres nécessite l'engagement sur le terrain de soixante hommes durant trois à cinq jours[81] - [82] - [43] - [83] - [84].

De 1858 à 1877, Carlos Ibáñez e Ibáñez de Ibero, qui dirigera l'Institut géographique d'Espagne dès sa fondation en 1870, conduit les opérations de triangulation de l'Espagne. Entre 1870 et 1894, François Perrier, puis Jean-Antonin-Léon Bassot procéderont à la mesure de la nouvelle méridienne de France en métropole et en Algérie. En 1879, François Perrier pour la France et Ibáñez pour l'Espagne réaliseront les travaux de jonction géodésique de l'Espagne avec l'Algérie en observant, depuis des stations d'altitude, des triangles allant jusqu'à 270 km de longueur et compléteront ainsi la mesure de la Méridienne de France par-dessus la Méditerranée, conformément au projet formulé par Biot et Arago. François Perrier annoncera à l'Académie des sciences en juillet 1879[34] - [Note 12].
« Si l'on jette les yeux sur une carte d'Europe, et que l'on considère l'immense série des travaux géodésiques qui couvrent actuellement d'un bout à l'autre les îles Britanniques, la France, l'Espagne et l'Algérie, on comprendra aussitôt combien il importait de relier entre eux ces grands réseaux de triangles pour en faire un tout allant de la plus septentrionale des îles Shetland, par 61° de latitude, jusqu'au grand désert d'Afrique, par 34°. Il s'agit là, en effet, du tiers à peu près de la distance de l'équateur au pôle. La mesure de son amplitude géodésique et astronomique devait être une des plus belles contributions que la Géodésie pût offrir aux géomètres pour l'étude de la figure du globe terrestre. Biot et Arago, à leur retour d'Espagne, avaient entrevu cette possibilité dans un lointain avenir, si jamais disaient-ils, la civilisation s'établissait de nouveau sur les rives qu'Arago avait trouvées si inhospitalières. Ce rêve, bien hardi, s'est pourtant réalisé ; l'Algérie devenue française a eu besoin d'une carte comme la France : la triangulation qui devait lui servir de base est terminée depuis des années ; nous venons de la rendre utile à la Science, en déterminant astronomiquement les points principaux. De son côté, l'Espagne terminait ses opérations géodésiques sur son territoire, en leur donnant une précision bien remarquable. Il ne restait donc plus qu'à franchir la Méditerranée par de grands triangles pour réunir d'un seul coup tous ces travaux. [...] Désormais, la Science possède un arc méridien de 27°, le plus grand qui ait été mesuré sur la Terre et projeté astronomiquement sur le ciel. »
Le point fondamental de la Nouvelle Méridienne de France est le Panthéon. Toutefois, le réseau géodésique ne suit pas exactement le méridien. Il dérive parfois à l'est et parfois à l'ouest. Selon les calculs effectués au Bureau central de l'Association géodésique par Friedrich Robert Helmert, le méridien de Greenwich est plus proche de la moyenne des mesures que le méridien de Paris. L'arc de méridien donne une valeur pour le rayon équatorial de la Terre a = 6 377 935 mètres, l’ellipticité supposée étant de 1/299,15. Le rayon de courbure de cet arc n'est pas uniforme, étant en moyenne d'environ 600 mètres plus grand dans la partie nord que dans la partie sud[17].
Prototype international du mètre

La détermination de la figure de la Terre par la mesure des arcs de méridiens repose sur l'hypothèse selon laquelle les parallèles de la Terre sont des cercles parfaits[85]. C'est pourquoi, en 1860, le gouvernement russe à l'initiative d'Otto Wilhelm von Stuve invite les gouvernements de Belgique, de France, de Prusse et le Royaume-Uni à connecter leurs triangulations afin de mesurer un arc de parallèle à la latitude de 52°. Il est alors nécessaire de comparer les différents étalons géodésiques utilisés dans chaque pays afin de combiner les mesures. Le gouvernement britannique invite ceux de France, de Belgique, de Prusse, de Russie, d'Inde, d'Australie, d'Autriche, d'Espagne, des États-Unis et du cap de Bonne-Espérance à envoyer leurs étalons géodésiques au bureau de l'Ordnance Survey à Southampton. Le mètre est l'unité de longueur géodésique en Espagne, aux États-Unis et en France, tandis que les étalons géodésiques utilisés en Prusse, en Belgique, en Russie, ainsi qu'en France sont calibrés sur la toise[37] - [38] - [75] - [32].
En 1866, Carlos Ibáñez e Ibáñez de Ibero offre à la Commission permanente de l'Association géodésique réunie à Neuchâtel deux de ses ouvrages traduits en français par Aimé Laussedat. Il s'agit des rapports des comparaisons de deux règles géodésiques calibrées sur le mètre construites pour l'Espagne et l'Égypte, entre elles et avec la règle N° 1 de la double toise de Borda qui sert de module de comparaison avec les autres étalons géodésiques et est alors la référence pour la mesure de toutes les bases géodésiques en France[86] - [87] - [88] - [75] - [32].
La Conférence générale de l'Association pour la mesure des degrés en Europe (qui deviendra l'Association internationale de géodésie) de 1867 appelle à la création d'un nouveau prototype international du mètre (PIM)[74] - [42] - [Note 13] et à l'arrangement d'un système où les étalons nationaux ainsi que toutes les règles géodésiques pourraient lui être comparés[39]. À la différence du mètre des Archives, le prototype international sera un étalon à traits ; ainsi, le mètre sera défini comme la distance entre deux lignes marquées sur la barre, évitant ainsi les problèmes d'usure liés à l'utilisation des étalons à bouts. La comparaison des étalons entre eux impliquera la création d'un appareillage spécial, ainsi que la définition d'une échelle de température reproductible[89]. En effet, la dilatation thermique qui correspond à l'expansion du volume d'un corps occasionné par son réchauffement est alors bien connue. Au XVIIIe siècle, le fameux physicien et géodésien Pierre Bouguer en avait fait la démonstration devant un large public à l'Hôtel des Invalides[90]. Ce problème a constamment dominé toutes les idées concernant la mesure des bases géodésiques. Les géodésiens sont occupés par la préoccupation constante de déterminer avec précision la température des étalons de longueur utilisés sur le terrain. La détermination de cette variable, dont dépend la longueur des instruments de mesure, a de tout temps été considérée comme si complexe et si importante qu'on pourrait presque dire que l'histoire des étalons géodésiques correspond à celle des précautions prises pour éviter les erreurs de température[91].
« Les relations intimes qui existent nécessairement entre la Métrologie et la Géodésie expliquent que l'Association internationale, fondée pour combiner et utiliser les travaux géodésiques des différents pays, afin de parvenir à une nouvelle et plus exacte détermination de la forme et des dimensions du Globe, ait donné naissance à l'idée de reformer les bases du Système métrique, tout en étendant celui-ci et le rendant international. Non pas, comme on l'a supposé par erreur pendant un certain temps, que l'Association ait eu la pensée peu scientifique de modifier la longueur du mètre, afin de la conformer exactement à sa définition historique d'après les nouvelles valeurs qu'on trouverait pour le méridien terrestre. Mais, occupés à combiner les arcs mesurés dans les différents pays et à rattacher les triangulations voisines, nous avons rencontré, comme une des principales difficultés, la fâcheuse incertitude qui régnait sur les équations des unités de longueur employées. Étant tombés d'accord avec le général Baeyer et le colonel Ibáñez, nous avons décidé, pour rendre comparables toutes les unités, de proposer à l'Association de choisir le mètre pour unité géodésique, de créer un Mètre prototype international différant aussi peu que possible du Mètre des Archives, de doter tous les pays d'étalons identiques et de déterminer de la manière la plus exacte les équations de tous les étalons employés en Géodésie, par rapport à ce prototype; enfin, pour réaliser ces résolutions de principe, de prier les gouvernements de réunir à Paris une Commission internationale du Mètre. Cette Commission fut en effet convoquée en 1870 ; mais, forcée par les événements de suspendre ses séances, elle n'a pu les reprendre utilement qu'en 1872. [...] Il serait oiseux d'insister […] sur les résolutions de principe votées par la Commission du Mètre ; il suffit de rappeler que, pour assurer l'exécution de ses décisions, elle avait recommandé aux Gouvernements intéressés la fondation à Paris d'un Bureau international des poids et mesures, et qu'elle a nommé une Commission permanente dont le général Ibáñez (il avait été promu en 1871 à l'emploi de général de brigade) a été élu président. En cette qualité de président de la Commission permanente, le général Ibáñez, appuyé par la grande majorité de ses collègues, a su vaincre, avec une fermeté admirable et infiniment de tact, tous les obstacles qui s'opposaient à la réalisation complète des décisions de la Commission du Mètre, et surtout à la création d'un Bureau international des poids et mesures. Les Gouvernements, convaincus de plus en plus de l'utilité d'une telle institution dans l'intérêt des sciences, de l'industrie et du commerce, se sont entendus pour convoquer au printemps de 1875 la Conférence diplomatique qui a abouti, le 20 mai de la même année, à la conclusion de la Convention du Mètre. Par la finesse déliée de son esprit diplomatique autant que par sa grande compétence scientifique, le général Ibáñez, qui représentait l'Espagne dans la Conférence, a contribué beaucoup à cet heureux résultat, qui devait assurer à plus de vingt États des deux mondes et à une population de 460 millions d'âmes la possession d'un système de Poids et Mesures métriques, d'une précision inconnue jusqu'alors, complètement identiques partout et offrant toutes les garanties d'inaltérabilité. »
— Adolphe Hirsch, Le général Ibáñez notice nécrologique lue au comité international des poids et mesures, le 12 septembre et dans la conférence géodésique de Florence, le 8 octobre 1891, Neuchâtel, imprimerie Attinger frères (« également disponible sur le site du BIPM »)
Le gouvernement français apporte son soutien à la création de la Commission internationale du mètre, qui se rassemble en 1870 puis en 1872 avec la participation d'une trentaine de pays[74]. Lors de la séance du 12 octobre 1872, Carlos Ibáñez e Ibáñez de Ibero est élu président du Comité permanent de la Commission internationale du mètre qui deviendra le Comité international des poids et mesures (CIPM)[92] - [75].
La Conférence diplomatique du mètre se réunit à Paris du 1er mars au 20 mai 1875. Deux camps sont en présence. Le premier souhaite la création d'un Bureau international des poids et mesures en France. Le second camp penche pour le maintien du statu quo en faveur du Conservatoire. La délégation française elle-même apparaît divisée entre la position de la République prônant la création du Bureau international des poids et mesures et la France du Conservatoire représentée par le général Morin. Dans un premier temps, la France adopte une position officielle neutre, tout en laissant le général Morin manœuvrer secrètement auprès des délégations étrangères dans l'intérêt du Conservatoire. Une troisième voie est envisagée, à savoir la création en Suisse du Bureau international des poids et mesures. Cette option semble d'emblée avoir peu de chance de succès en raison du fort soutien de l'Espagne et de l'Italie à la création du Bureau international à Paris. Après un ultimatum de Wilhelm Foerster, le délégué allemand, la délégation française se positionne officiellement en faveur de la création du Bureau international des poids et mesures[93].
La présidence du géodésien espagnol sera confirmée lors de la première séance du Comité international des poids et mesures, le [94]. Deux autres membres du Comité, le Suisse Heinrich von Wild représentant la Russie et le géodésien suisse d'origine allemande Adolphe Hirsch comptent également au nombre des principaux architectes de la Convention du mètre[95] - [96] - [97] - [98] - [75].
La Conférence générale de l'Association géodésique, réunie en marge de la Conférence diplomatique du mètre, décide la création d'une règle géodésique internationale pour la mesure des bases[33].

La nature internationale des nouveaux étalons du mètre est assurée par un traité, la Convention du mètre, signée à Paris le . Le traité établit une organisation internationale, le Bureau international des poids et mesures (BIPM), pour conserver les prototypes — qui deviennent propriétés conjointes des nations signataires — et pour effectuer des comparaisons régulières avec les étalons nationaux. En reconnaissance du rôle de la France dans la conception du système métrique, le BIPM est basé à Sèvres, près de Paris. Cependant, en tant qu'organisation internationale, le BIPM est sous le contrôle ultime d'une conférence diplomatique, la Conférence générale des poids et mesures (CGPM), plutôt que du gouvernement français[13] - [99].
La construction du prototype international du mètre et des étalons nationaux constitue un problème technique majeur à l’époque. Les règles prismatiques sont faites d'un alliage spécial, 90 % de platine et 10 % d'iridium, considérablement plus dur que le platine pur, et avec une section en croix particulière (une section de Tresca, nommée d'après l'ingénieur français Henri Tresca) pour minimiser les effets de torsion pendant les comparaisons de longueur[13]. Les premières fontes sont jugées insatisfaisantes et l'ouvrage est confié à la firme londonienne Johnson Matthey, qui parvient à produire 30 règles respectant les spécifications requises. La longueur de l'une d'elles, portant le no 6, est déterminée comme étant identique à celle du mètre des Archives. La règle no 6 est désignée comme prototype international du mètre à la première rencontre de la CGPM de 1889. Les autres règles, dont les équations, par rapport au prototype international, sont renfermées dans la limite de 0,01 millimètre (avec une erreur probable ne dépassant pas ± 0,0002 millimètre) sont distribuées aux pays signataires de la Convention du mètre pour être utilisées comme étalons nationaux[80]. Par exemple, les États-Unis reçoivent la règle no 27 d'une longueur étalonnée à 1 m − 1,6 µm + 8,657 µm*T + 0,001 µm*T2 ±0,2 µm[100]. Les États contractants reçoivent également une collection de thermomètres dont la précision permet d'assurer celle des mesures de longueur[80].
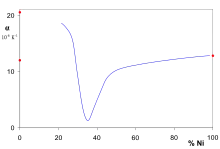
Les relations entre la métrologie et la géodésie se poursuivent après la création du Bureau international des poids et mesures, comme en témoigne l'attribution, en 1920, du prix Nobel au physicien suisse Charles Édouard Guillaume pour ses travaux sur l'invar. L'invar est un alliage de fer (64 %) et de nickel (36 %) dont la propriété principale est un coefficient de dilatation très faible. Cette propriété permet l'utilisation de l'invar pour effectuer des mesures de haute précision sur le terrain, dans des conditions soumises à d'importantes variations de température[101].
« Depuis l'immortel travail de Delambre et Méchain, la mesure des bases n'avait fait que peu de progrès. Ibáñez voulut d'abord perfectionner le procédé des règles bimétalliques, de Borda et Lavoisier, employées, sous une forme encore un peu fruste, dans la mesure de la Méridienne de France, et fit construire, par les frères Brunner, un appareil qui passa pendant un temps pour le plus parfait qui eût été réalisé ; des répliques en furent construites, pour plusieurs des grands États de l'Europe, ainsi que pour l'Égypte. Le Bureau international en a fait une, étude minutieuse.
Mais le maniement de la règle bimétallique était délicat, et la mesure des bases trop coûteuse, en rapport avec l'ensemble du travail, Ibáñez revint donc à la règle monométallique en fer, accompagnée de thermomètres, dont la donnée subsista jusqu'à l'introduction des règles en invar bientôt remplacées à leur tour par la méthode de Jäderin, qui, transformée par l'emploi des fils d'invar, put prendre rang dans la géodésie de précision, sous une forme incomparablement plus économique que tous les anciens procédés. »
— Charles Édouard Guillaume, « Notice nécrologique de F. da Paula Arrillaga y Garro ».
Edvard Jäderin (sv), un géodésien suédois, invente un procédé de mesure des bases, fondé sur l'utilisation de fils tendus sous un effort constant. Toutefois, avant la découverte de l'invar, ce procédé est nettement moins précis que la méthode classique de la règle. En 1900, le Comité international des poids et mesures donne suite à une demande de l'Association géodésique internationale et inscrit au programme des travaux du Bureau international des poids et mesures l'étude des mesures par les fils d'invar. Charles Édouard Guillaume démontre l'efficacité de la méthode de Jäderin, améliorée par l'utilisation des fils d'invar. Il mesure une base dans le tunnel du Simplon en 1905. La précision des mesures est égale à celle des anciennes méthodes, alors que la rapidité et la facilité des mesures sont incomparablement plus élevées[101] - [43].
La première (et unique) comparaison ultérieure des copies nationales avec le prototype international est menée entre 1921 et 1936[13] - [42], et indique que la définition du mètre est préservée à 0,2 µm près[102]. À l'époque, il s'avère qu'une définition plus formelle du mètre est nécessaire (la décision de 1889 disait seulement : « le prototype représentera désormais, à la température de la glace fondante, l'unité métrique de longueur »), ce qui est décidé lors de la 7e CGPM en 1927[103].
« L'unité de longueur est le mètre, défini par la distance, à 0°, des axes des deux traits médians tracés sur la barre de platine iridié déposée au Bureau international des poids et mesures, et déclarée Prototype du mètre par la Première Conférence générale des poids et mesures, cette règle étant soumise à la pression atmosphérique normale et supportée par deux rouleaux d'au moins un centimètre de diamètre, situés symétriquement dans un même plan horizontal et à la distance de 571 mm l'un de l'autre. »
Les spécifications concernant le soutien de la barre correspondent aux points d'Airy (en) du prototype — les points sont séparés par une distance correspondant au 4⁄7 de la longueur totale de la barre, de manière que sa flexion soit réduite au minimum[104].
Les efforts pour combiner les différents travaux géodésiques nationaux qui débutent au XIXe siècle avec la fondation de l'Association géodésique internationale auront pour résultat une série d’ellipsoïdes globaux de la Terre (p. ex. : Helmert 1906, Hayford 1910/1924) qui conduiront plus tard au développement de systèmes géodésiques mondiaux.
La définition actuelle du mètre est liée à la vitesse de la lumière, qui équivaut à 299 792 458 mètres par seconde. De nos jours, la réalisation pratique du mètre est rendue possible grâce aux horloges atomiques embarquées dans les satellites GPS.
Définition à partir du krypton
Les premières mesures interférométriques menées avec le prototype international du mètre sont celles d'Albert A. Michelson et Jean-René Benoît (1892–1893)[105] et de Benoît, Fabry et Perot (1906)[106], toutes deux utilisant la ligne rouge du cadmium. Ces résultats, qui utilisent la longueur d'onde de la ligne du cadmium (λ ≈ 644 nm), ont mené à la définition de l’ångström comme unité secondaire de longueur pour des mesures spectroscopiques, d'abord par l'Union internationale en faveur de la coopération pour la recherche solaire (en) (1907)[107] puis par le CIPM (1927)[42] - [108] - [Note 14]. Le travail de Michelson sur la « mesure » du mètre-étalon à moins d'un dixième de longueur d'onde (<0,1 µm) est une des raisons de son prix Nobel de physique en 1907[13] - [42] - [109].
Dans les années 1950, l’interférométrie est devenue la méthode de choix pour des mesures précises de longueur, mais il demeurait un problème pratique imposé par le système d'unités utilisé. L'unité naturelle pour exprimer une longueur mesurée par l'interférométrie est l'ångström, mais ce résultat devait être converti en mètres par un facteur de conversion expérimental – la longueur d'onde de la lumière utilisée mesurée non pas en ångströms mais en mètres. Ceci ajoutait une incertitude de mesure supplémentaire pour chaque résultat de longueur en mètres, a priori et a posteriori de la mesure interférométrique effective. La solution était de définir le mètre de la même façon que l'ångström avait été défini en 1907, à savoir selon la meilleure mesure interférométrique disponible.
Les avancées en technique expérimentale et en théorie ont montré que la ligne du cadmium est en réalité un groupe de lignes très rapprochées, en raison de la présence de différents isotopes dans le cadmium naturel (8 en tout). Pour obtenir la ligne la plus précise, il est nécessaire d'utiliser une source mono-isotopique et cette source doit contenir un isotope avec un nombre pair de protons et de neutrons (pour avoir un spin nul)[13]. Plusieurs isotopes du cadmium, du krypton et du mercure remplissent cette condition de spin nul et ont des lignes claires dans le spectre visible de la lumière. À température ambiante, le krypton est un gaz permettant un enrichissement isotopique plus simple et des températures d'opération plus basses pour la lampe (réduisant ainsi l'élargissement de la ligne par effet Doppler), aussi la ligne orange de l’isotope 86 du krypton (λ ≈ 606 nm) est choisie comme longueur d'onde standard[13] - [110]. Ainsi, la 11e CGPM de 1960 décide d'une nouvelle définition du mètre[111]:
« Le mètre est la longueur égale à 1 650 763,73 longueurs d'onde dans le vide de la radiation correspondant à la transition entre les niveaux 2p10 et 5d5 de l'atome de krypton 86. »
La mesure de la longueur d'onde de la ligne du krypton n'a pas été comparée directement au prototype international du mètre ; au lieu de cela, le rapport de la longueur d'onde dans le vide de la ligne du krypton sur celle de la ligne du cadmium a été déterminée. Il a ensuite été comparé à la longueur d'onde de la ligne du cadmium dans l’air (avec correction pour l'indice de réfraction de l'air), déterminée en 1906 par Fabry et Perot[13] - [102]. Ce procédé a rendu possible une traçabilité vis-à-vis du prototype du mètre et également vis-à-vis de l'ancienne définition de l’ångström.
Définition à partir de la lumière

La lampe à décharge du krypton-86 fonctionnant au point triple de l'azote (63,14 K, −210,01 °C) était la source de lumière de base dans l’état de l'art de l'interférométrie en 1960, mais elle fut vite dépassée par une nouvelle invention : le laser, dont la première version de travail a été construite la même année que la redéfinition du mètre[112]. La lumière du laser est habituellement très monochromatique, et également cohérente (toute la lumière a la même phase, contrairement à la lumière d'une lampe à décharge), deux avantages pour l'interférométrie[13].
Les limites de l'étalon basé sur le krypton ont été démontrées par la mesure de la longueur d'onde de la lumière d'un laser hélium-néon stabilisé par méthane (λ ≈ 3,39 µm). La ligne du krypton s'est avérée asymétrique, ainsi différentes longueurs d'onde pouvaient être trouvées pour le laser selon le point sur la ligne du krypton prise comme référence[Note 15]. L'asymétrie affecte aussi la précision pour laquelle les longueurs peuvent être mesurées[113] - [114].
Les développements en électronique ont aussi rendu possible, pour la première fois, la mesure de la fréquence de la lumière dans des régions proches du spectre visible, au lieu d'induire la fréquence par la longueur d'onde et la vitesse de la lumière. Bien que les fréquences des ondes visibles et infrarouges fussent toujours trop hautes pour être mesurées, il était possible de construire une « chaîne » de fréquences de laser qui, par un facteur adapté, diffèrent de chacune d'une fréquence directement mesurable dans la région des micro-ondes. La fréquence de la lumière du laser stabilisé au méthane a été mesurée à 88,376 181 627(50) THz[113] - [115].
Les mesures indépendantes de fréquence et de longueur d'onde reviennent à mesurer la vitesse de la lumière (c = fλ), et les résultats par le laser stabilisé au méthane ont donné une valeur pour la vitesse de la lumière avec une incertitude de mesure presque 100 fois plus petite que les mesures précédentes dans la région des micro-ondes. Dans les faits, les résultats ont donné deux valeurs pour la vitesse de la lumière, selon le point choisi sur la ligne du krypton pour définir le mètre[Note 16]. Cette ambiguïté a été résolue en 1975 quand la 15e CGPM a approuvé une valeur conventionnelle de la vitesse de la lumière d'exactement 299 792 458 m s−1[116].
Néanmoins, la lumière infrarouge d'un laser stabilisé au méthane n'était pas idéale pour l'interférométrie. C'est en 1983 que la chaîne de mesures de fréquences a atteint la ligne de 633 nm du laser hélium-néon, stabilisé par de l'iode[117] - [118]. La même année, la 17e CGPM adopte la définition actuelle du mètre, selon la valeur conventionnelle de la vitesse de la lumière fixée en 1975[119]:
« Le mètre est la longueur du trajet parcouru dans le vide par la lumière pendant une durée de 1⁄299792458 de seconde. »
Le concept de définir une unité de longueur selon une unité de temps a été critiquée[120], bien qu'elle soit similaire à la proposition originale de John Wilkins, en 1668, qui définissait l'unité de longueur universelle par le pendule simple. Dans les deux cas, le problème pratique est que le temps peut être mesuré plus précisément que la distance (une partie en 1013 pour une seconde en utilisant une horloge au césium au lieu de quatre parties en 109 pour le mètre en 1983)[108] - [120]. La définition en termes de vitesse de la lumière signifie aussi que le mètre peut être mesuré en utilisant n'importe quelle source de lumière de fréquence connue, au lieu de définir une source précise à l'avance. Sachant qu'il y a plus de 22 000 lignes dans le spectre visible de l’iode, dont l'une quelconque pourrait être utilisée pour stabiliser une source laser, les avantages de la flexibilité sont évidents[120].
Notes
- Jean Picard mesure un arc de méridien entre Paris et Amiens en 1669-1670. Il trouve qu'un degré de latitude correspond à une distance terrestre de 57060 toises de Paris. Il en déduit que la circonférence de la Terre ou le périmètre du cercle passant par les pôles est égal à 20541600 toises de Paris. Il calcule que le diamètre de la Terre équivaut à 6538594 toises de Paris, soit un rayon d'environ 6365,6 km.
- À l'époque un méridien était considéré comme faisant le tour de la Terre. Aujourd'hui un méridien va du pôle Nord au pôle Sud, si bien que le mètre est approximativement égal à la 10 000 000e partie d'un demi-méridien.
- Il s'avère par coïncidence que cette grandeur est proche de celle du pendule battant la seconde à une latitude de 45° et au niveau de la mer, puisque celle-ci vaut 0,993 977 m.
- Le Prototype international du mètre constitue la base du nouveau système international d'unités, mais il n'a plus aucune relation avec les dimensions de la Terre que les géodésiens s'efforcent de déterminer au XIXe siècle. Il n'est plus que la représentation matérielle de l'unité du système.
- Si la métrologie de précision a profité des progrès de la géodésie, celle-ci ne peut continuer à prospérer sans le concours de la métrologie. En effet, toutes les mesures d'arcs terrestres et toutes les déterminations de la force de gravité par le pendule doivent impérativement être exprimées dans une unité commune. La métrologie se doit donc de créer une unité adoptée et respectée par toutes les nations de façon à pouvoir comparer avec la plus grande précision toutes les règles ainsi que tous les battants des pendules employés par les géodésiens.
- L'idée du pendule battant la seconde comme étalon de longueur n'a pas totalement disparu. En effet, en 1824 le parlement britannique confirmait l'étalon du yard de 1760. Toutefois, il précisait que si cet étalon en laiton devait être détruit (ce qui arriva le 16 octobre 1834), il pourrait être restauré sur la base de son rapport avec la longueur du pendule à secondes mesurée à Londres au niveau de la mer et dans le vide.
- Les valeurs en lignes se réfèrent à la toise de Pérou, et non à la valeur liée aux mesures usuelles. 1 toise = 6 pieds ; 1 pied = 12 pouces ; 1 pouce = 12 lignes ; soit 864 lignes = 1 toise.
- Distances données par Google Earth. Les coordonnées sont :
51° 02′ 08″ N, 2° 22′ 34″ E – Beffroi de Dunkerque
44° 25′ 57″ N, 2° 34′ 24″ E – Cathédrale de Rodez
41° 21′ 48″ N, 2° 10′ 01″ E – Montjuïc, Barcelone - Le sphéroïde de référence WGS 84 a un demi-axe majeur de 6 378 137,0 m et un aplatissement de 1⁄298.257223563.
- Les résultats de la principale triangulation du Royaume-Uni ont été publiés en 1858 par l'Ordnance Survey sous le titre : (en) « Account of the observations and calculation of the principal triangulation; and of the figure, dimensions and mean specific gravity of the Earth derived therefrom. », sur google livre, (consulté le )
- Les travaux de jonction des triangulations anglaise et française ont été répétés en 1861-1862 et publiés par l'Ordnance Survey en 1863 sous le titre : (en) « Extension of the Triangulation of the Ordnance Survey into France and Belgium with the measurement of an arc of parallel in latitude 52° from Valentia in Ireland to mount Kemmel in Belgium. », sur google livre, (consulté le )
- Le compte rendu des travaux de jonction des triangulations espagnole et algérienne a été publié par le Général Ibáñez et le Colonel Perrier, Jonction géodésique et astronomique de l'Algérie avec l'Espagne, Paris, Imprimerie nationale, (lire en ligne)
- Le terme « prototype » n'est pas à comprendre comme le premier d'une série et que d'autres suivront, mais comme le premier produit qui servira de référence de comparaison pour les suivants.
- L'IUSR (renommée plus tard l'Union astronomique internationale) définit l'ångström de telle sorte que la longueur d'onde (dans l’air) de la ligne du cadmium soit de 6 438,469 63 Å.
- En prenant le point de plus forte intensité comme longueur d'onde référence, la ligne du méthane en une longueur d'onde de 3,392 231 404(12) µm ; en prenant le point d'intensité moyenne (« centre de gravité ») de la ligne du krypton comme référence, la mesure devient 3,392 231 376(12) µm.
- La vitesse de la lumière mesurée est de 299 792,456 2(11) km s−1 pour le « centre de gravité » et 299 792,458 7(11) km s−1 pour le point d'intensité maximale, avec une incertitude relative de ur= 3,5 × 10−9.
Références
- (en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « History of the metre » (voir la liste des auteurs).
- (en) François Cardarelli, Encyclopaedia of Scientific Units, Weights and Measures : Their SI Equivalences and Origins, Springer-Verlag London Ltd., , 848 p. (ISBN 978-1-4471-1122-1)
- Du pied au mètredu marc au kiloL’histoire des unités des poids et mesuresévoquée par quelques objets emblématiques descollections du Musée d’histoire des sciences, Genève, Musée d’histoire des sciences, Genève, , 25 p. (lire en ligne), p. 2
- Zaide Duran et Umut Aydar, « Digital modeling of world's first known length reference unit: The Nippur cubit rod », Journal of Cultural Heritage, vol. 13, no 3, , p. 352–356 (ISSN 1296-2074, DOI 10.1016/j.culher.2011.12.006, lire en ligne, consulté le )
- (en) Z. Duran et U. Aydar, Measurement and 3D modelling of an ancient measuring device : Nippur Cubit Rod, Beijing, The International Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences., , 265-269 p. (lire en ligne), p. 265
- Grand dictionnaire universel du XIXe siècle, vol. 11, Paris, Pierre Larousse, 1866–77 (lire en ligne), « Métrique », p. 163–164
- Clara Agustoni et Carmen (préf) Buchillier, Des chiffres ou des lettres : compter, calculer, mesurer à l'époque romaine, Musée romain Vallon, coll. « Musée romain Vallon », (lire en ligne), p. 43, 32
- Chevalier De Jaucourt, « Enccre/ICE - Interface de Consultation de l'Édition numérique collaborative et critique de l'Encyclopédie : Article Pié, (Mesure de longueur.), vol. XII (1765), p. 562a–463 [563b »], sur enccre.academie-sciences.fr (consulté le ), p. 463
- « Enccre/ICE - Interface de Consultation de l'Édition numérique collaborative et critique de l'Encyclopédie : Article Mesure longue, (Antiq. Arts & Comm.), vol. X (1765), p. 411b–418a », sur enccre.academie-sciences.fr (consulté le ), p. 411, 413
- Chambers, « Enccre/ICE - Interface de Consultation de l'Édition numérique collaborative et critique de l'Encyclopédie : Article Perche, (Arpent.), vol. XII (1765), p. 329a », sur enccre.academie-sciences.fr (consulté le )
- La Chapelle, « Enccre/ICE - Interface de Consultation de l'Édition numérique collaborative et critique de l'Encyclopédie : Article Arpent, (Agricult.), vol. I (1751), p. 702a », sur enccre.academie-sciences.fr (consulté le )
- La Chapelle et Mallet, [http://enccre.academie-sciences.fr/encyclopedie/export-article/v1-474-1/ « Enccre/ICE - Interface de Consultation de l'Édition numérique collaborative et critique de l'Encyclopédie : Article Acre, (Commerce.), vol. I (1751), p. 113a Transcription »], sur enccre.academie-sciences.fr (consulté le )
- « Enccre/ICE - Interface de Consultation de l'Édition numérique collaborative et critique de l'Encyclopédie : Article AUNE, (Commerce.), vol. I (1751), p. 882b–883a », sur enccre.academie-sciences.fr (consulté le )
- Robert A. Nelson, Foundations of the international system of units (SI), coll. « The Physics Teacher », (lire en ligne), p. 596–613
- (en) John Wilkins, An Essay Towards a Real Character, And a Philosophical Language, Londres, Gillibrand, (lire en ligne), p. 190-192
- (it) Tito Livio Burattini et Ludwik Antoni Birkenmajer, Misura Universale,
- (en) P. Agnoli et G. D'Agostini, « Why does the meter beat the second », Publication en ligne, (lire en ligne)
- (en) Clarke, Alexander Ross et Helmert, Friedrich Robert, « Earth, Figure of the », 1911 Encyclopædia Britannica, vol. 8, , p. 801-814 (lire en ligne, consulté le )
- Jean-Jacques Levallois, La Vie des sciences : L'Académie royale des Sciences et la Figure de la Terre, Diffusion centrale des revues, (lire en ligne), p. 261-301
- Guillaume Bigourdan, Le système métrique des poids et mesures ; son établissement et sa propagation graduelle, avec l'histoire des opérations qui ont servi à déterminer le mètre et le kilogramme, Paris : Gauthier-Villars, (lire en ligne), p. 6-8, 14-17, 148-154
- Jean Picard, Mesure de la terre [par l'abbé Picard], Impr. royale, (lire en ligne), p. 3-5, 23
- John Henry Poynting et Joseph John Thompson, A Textbook of Physics : Properties of Matter, Londres, Charles Griffin, , 4e éd. (lire en ligne), p. 20
- Alexis-Jean-Pierre Paucton, Métrologie ou Traité des mesures, poids et monnoies des anciens peuples & des modernes, (lire en ligne), p. 102-103
- Béatrice Sandre, « INRP - CLEA - Archives : Fascicule no 137, Printemps 2012 Les distances », sur clea-astro.eu, Cahier Clairaut, (consulté le ), p. 17-20
- « Première détermination de la distance de la Terre au Soleil | Les 350 ans de l'Observatoire de Paris », sur 350ans.obspm.fr (consulté le )
- Vincent Deparis, « La découverte historique de la variation de la pesanteur avec la latitude », sur https://planet-terre.ens-lyon.fr/,
- Élisabeth Badinter, Les passions intellectuelles, Paris, Robert Laffont, , 1206 p. (ISBN 978-2-221-20345-3, OCLC 1061216207, lire en ligne)
- D'Alembert, « Enccre/ICE - Interface de Consultation de l'Édition numérique collaborative et critique de l'Encyclopédie : Figure de la Terre, (Astron. Géog. Physiq. & Méch.), vol. VI (1756), p. 749b–761b », sur enccre.academie-sciences.fr, (consulté le ), p. 752
- « Histoire du mètre », Direction Générale des Entreprises (DGE), (lire en ligne, consulté le )
- (en) Madhvi Ramani, « How France created the metric system », sur www.bbc.com (consulté le )
- Jacques-Paul Migne, Encyclopédie théologique, Dictionnaire des inventions et découvertes, vol. 36, , 1417 p. (lire en ligne), p. 417-419.
- (en) Nomination of the Struve geodetic arc for inscription on the World Heritage List, , 294 p. (lire en ligne), p. 29
- (en) T. Soler, « A profile of General Carlos Ibáñez e Ibáñez de Ibero: first president of the International Geodetic Association », Journal of Geodesy, vol. 71, no 3, , p. 176–188 (ISSN 0949-7714 et 1432-1394, DOI 10.1007/s001900050086, lire en ligne, consulté le )
- Ernest (1846-1922) Auteur du texte Lebon, Histoire abrégée de l'astronomie : par Ernest Lebon,..., Gauthier-Villars, (lire en ligne), p. 171-172
- François Perrier, Comptes rendus hebdomadaires des séances de l'Académie des sciences : publiés... par MM. les secrétaires perpétuels, Gauthier-Villars, (lire en ligne), p. 885
- Carlos (1825-1891) Auteur du texte Ibáñez e Ibáñez de Íbero et François (1833-1888) Auteur du texte Perrier, Jonction géodésique et astronomique de l'Algérie avec l'Espagne, exécutée en commun en 1879, par ordre des gouvernements d'Espagne et de France, sous la direction de M. le général Ibañez,... pour l'Espagne, M. le colonel Perrier,... pour la France, (lire en ligne)
- Jean Coulomb, Géophysique in Encyclopædia universalis. Corpus., Paris, Encyclopædia universalis, (ISBN 2-85229-290-4 et 9782852292901, OCLC 36747385, lire en ligne), p. 370. Vol. 10
- (en) Alexander Ross Clarke, « X. Abstract of the results of the comparisons of the standards of length of England, France, Belgium, Prussia, Russia, India, Australia, made at the ordnance Survey Office, Southampton », Philosophical Transactions of the Royal Society of London, vol. 157, , p. 161–180 (ISSN 0261-0523, DOI 10.1098/rstl.1867.0010, lire en ligne, consulté le )
- (en) Alexander Ross Clarke et Henry James, « XIII. Results of the comparisons of the standards of length of England, Austria, Spain, United States, Cape of Good Hope, and of a second Russian standard, made at the Ordnance Survey Office, Southampton. With a preface and notes on the Greek and Egyptian measures of length by Sir Henry James », Philosophical Transactions of the Royal Society of London, vol. 163, , p. 445–469 (ISSN 0261-0523, DOI 10.1098/rstl.1873.0014, lire en ligne, consulté le )
- Adolphe Hirsch, Le Général Ibáñez : Notice nécrologique lue au Comité international des poids et mesure, le 12 septembre et dans la conférence géodésique de Florence, le 8 octobre 1891, Neuchâtel, Imprimerie Attinger Frères, , 15 p. (lire en ligne)
- « BIPM - La Commission internationale du mètre », sur www.bipm.org (consulté le )
- « BIPM - la définition du mètre », sur www.bipm.org (consulté le )
- « Le BIPM et l'évolution de la définition du mètre », Bureau international des poids et mesures (consulté le )
- Ch.-Ed Guillaume, « La mesure rapide des bases géodésiques », Journal de Physique Théorique et Appliquée, vol. 5, no 1, , p. 242–263 (ISSN 0368-3893, DOI 10.1051/jphystap:019060050024200, lire en ligne, consulté le )
- (es) Carlos Ibáñez e Ibáñez de Ibero, Discursos leidos ante la Real Academia de Ciencias Exactas Fisicas y Naturales en la recepcion pública de Don Joaquin Barraquer y Rovira, Madrid, Imprenta de la Viuda e Hijo de D.E. Aguado, , 80 p. (lire en ligne), p. 70-78
- « Le mètre, l'aventure continue... » (consulté le )
- Peter Bond (trad. de l'anglais), L'exploration du système solaire, Paris/Louvain-la-Neuve, De Boeck, dl 2014, cop. 2014, 462 p. (ISBN 978-2-8041-8496-4 et 280418496X, OCLC 894499177, lire en ligne), p. 5-6
- « Distance Terre-Soleil : lunité astronomique définitivement établie », Gentside Découverte, (lire en ligne, consulté le )
- « 1967LAstr..81..234G Page 234 », sur adsbit.harvard.edu (consulté le ), p. 236-237
- « toise — Wiktionnaire », sur fr.wiktionary.org (consulté le )
- Pierre Portet Lamop Université de Paris I, « La mesure de Paris », Les anciennes mesures du Centre historique de la France d’après les tables de conversion, Charbonnier, Pierre (éd.), Editions du CTHS, Paris, 2012, pp. 13-54., 2012., , p. 12-14 (lire en ligne, consulté le )
- Isaac Newton, Principes mathématiques de la philosophie naturelle [traduit du latin] par feue madame la marquise Du Chastellet [Avec une préface de Roger Cotes et une préface de Voltaire]. T. 2, Desaint et Saillant, (lire en ligne), p. 13
- Cassidy, David C. (1945- ...)., Rutherford, Floyd James, (1924- ...)., Faye, Vincent. et Bréard, Sébastien. (trad. de l'anglais), Comprendre la physique, Lausanne, Presses polytechniques et universitaires romandes, cop. 2014, 812 p. (ISBN 978-2-88915-083-0, OCLC 895784336, lire en ligne)
- (en) Murdin, Paul., Full meridian of glory : perilous adventures in the competition to measure the earth, New-York, Copernicus Books/Springer, , 187 p. (ISBN 978-0-387-75533-5, OCLC 314175913, lire en ligne), p. 39-75
- Denis Février, « Histoire du mètre », sur entreprises.gouv.fr (consulté le )
- « ETH-Bibliothek / Base du système métrique... [30] », sur www.e-rara.ch (consulté le ), tome 2, page [30] 2 ; tome 3, page [438] 414 ; tome 3, page [337] 313
- (en) Jean-Pierre Martin et Anita McConnell, « Joining the observatories of Paris and Greenwich », Notes and Records, vol. 62, no 4, , p. 355–372 (ISSN 0035-9149 et 1743-0178, DOI 10.1098/rsnr.2008.0029, lire en ligne, consulté le )
- César-François Cassini de Thury, Description géométrique de la France, J. Ch. De saint, (lire en ligne)
- « Wayback Machine », (version du 18 avril 2007 sur Internet Archive)
- « A Note on the History of the IAG », sur IAG Homepage (consulté le )
- (en) W. Torge, « The International Association of Geodesy 1862 to 1922: from a regional project to an international organization », Journal of Geodesy, vol. 78, no 9, , p. 558–568 (ISSN 0949-7714 et 1432-1394, DOI 10.1007/s00190-004-0423-0, lire en ligne, consulté le )
- (es) Mario Ruiz Morales, « Libros digitales : La medida de la Tierra entre 1816 y 1855, Centro Nacional de Informacíon Geográfica (CNIG), 2015, 393 p. », sur Geoportal oficial del Instituto Geográfico Nacional de España (consulté le ), p. 7
- Ken Alder (trad. de l'anglais), Mesurer le monde : 1792-1799 : l'incroyable histoire de l'invention du mètre, Paris, Flammarion, , 469 p. (ISBN 2-08-210328-5 et 9782082103282, lire en ligne), p. 338-339, 366-367, 71-74
- Gustave Moynier, Les bureaux internationaux des unions universelles : par Gustave Moynier,..., A. Cherbuliez, (lire en ligne), p. 99-107
- (en) Wolfgang Torge, IAG 150 Years, Springer, Cham, coll. « International Association of Geodesy Symposia », (ISBN 978-3-319-24603-1 et 9783319308951, DOI 10.1007/1345_2015_42, lire en ligne), p. 3–18
- (en) Charles Hutton Dowling, A Series of Metric Tables, in which the British Measures and Weights are Compared with Those of the Metric System at Present in Use on the Continent, Lockwood, (lire en ligne)
- (en) Great Britain, The Statutes of the United Kingdom of Great Britain and Ireland, His Majesty's Statute and Law Printers, (lire en ligne)
- J. J. O'Connor et E. F. Robertson, « Jean Charles de Borda », School of Mathematics and Statistics, University of St. Andrews, Scotland, (consulté le )
- National Industrial Conference Board, The metric versus the English system of weights and measures..., The Century Co., (lire en ligne), p. 10–11
- Ken Alder, The Measure of all Things – The Seven-Year-Odyssey that Transformed the World, Londres, Abacus, (ISBN 0-349-11507-9), p. 227–230
- Ken Alder, The Measure of all Things – The Seven-Year-Odyssey that Transformed the World, Londres, Abacus, (ISBN 0-349-11507-9), p. 240–241
- Loi du 19 frimaire an VIII (Octave Gréard, La législation de l'instruction primaire en France depuis 1789 jusqu'à nos jours, tome 2, p. 324): La Commission, après avoir déclaré l'urgence, prend la résolution suivante : Article 1er - La fixation provisoire de la longueur du mètre, à trois pieds onze lignes quarante-quatre centièmes, ordonnée par les lois du 1er août 1793 et du 18 germinal an III, demeure révoquée et comme non avenue. Ladite longueur, formant la dix-millionième partie de l'arc du méridien terrestre compris entre le pôle nord et l'équateur, est définitivement fixée, dans son rapport avec les anciennes mesures, à trois pieds onze lignes deux cent quatre-vingt-seize millièmes. Article 2 - Le mètre et le kilogramme en platine, déposés le 4 messidor dernier au Corps législatif par l'Institut national des sciences et des arts, sont les étalons définitifs des mesures de longueur et de poids dans toute la République. Il en sera remis à la commission consulaire des copies exactes pour servir à diriger la confection des nouvelles mesures et des nouveaux poids.
- Jean-Baptiste (1774-1862) Auteur du texte Biot et François (1786-1853) Auteur du texte Arago, Recueil d'observations géodésiques, astronomiques et physiques, exécutées par ordre du Bureau des longitudes de France en Espagne, en France, en Angleterre et en Écosse, pour déterminer la variation de la pesanteur et des degrés terrestres sur le prolongement du méridien de Paris... rédigé par MM. Biot et Arago,..., Vve Courcier, (lire en ligne)
- Louis Puissant, « Comptes rendus hebdomadaires des séances de l'Académie des sciences / publiés... par MM. les secrétaires perpétuels », sur Gallica, (consulté le ), p. 428-433
- La Commission internationale du mètre (1870-1872), Bureau international des poids et mesures (lire en ligne)
- Suzanne Débarbat et Terry Quinn, « Les origines du système métrique en France et la Convention du mètre de 1875, qui a ouvert la voie au Système international d'unités et à sa révision de 2018 », Comptes Rendus Physique, the new International System of Units / Le nouveau Système international d’unités, vol. 20, no 1, , p. 6–21 (ISSN 1631-0705, DOI 10.1016/j.crhy.2018.12.002, lire en ligne, consulté le )
- Hevé Faye, « Comptes rendus hebdomadaires des séances de l'Académie des sciences / publiés... par MM. les secrétaires perpétuels : Rapport sur un mémoire de M. Peirce concernant la constante de la pesanteur à Paris et les corrections exigées par les anciennes déterminations de Borda et de Biot. », sur Gallica, (consulté le ), p. 1463-1466
- (en) « NIST Special Publication 1068 Ferdinand Rudolph Hassler (1770-1843) A Twenty Year Retrospective, 1987-2007 », sur https://www.nist.gov/, (consulté le )
- « Ferdinand Rudolf Hassler 1770-1843 Pionnier suisse pour la mensuration, la cartographie et les poids et mesures aux Etats-Unis », sur e-expo: Ferdinand Rudolf Hassler, (consulté le )
- Gustave Moynier, Les bureaux internationaux des unions universelles : par Gustave Moynier,..., A. Cherbuliez, (lire en ligne), p. 60
- CGPM : Compte rendu de la 1re réunion (1889) (lire en ligne), p. 55, 35, 25-28
- Brunner, Comptes rendus hebdomadaires des séances de l'Académie des sciences / publiés... par MM. les secrétaires perpétuels. Géodésie. : Appareil construit pour les opérations au moyen desquelles on prolongera dans toute l'étendue de l'Espagne le réseau trigonométrique qui couvre la France, Paris, Gauthier-Villars, (lire en ligne), p. 150-152
- Charles-Édouard Guillaume, Notice nécrologique de F. da Paula Arrillaga y Garro, Paris (lire en ligne), p. 110
- « Geodesy », 1911 Encyclopædia Britannica, vol. 11, (lire en ligne, consulté le )
- A. Hirsch et J. Dumur, Le Réseau de Triangulation Suisse, Lausanne, Commission Géodésique Suisse, , 116 p. (lire en ligne)
- Jean Le Rond d'Alembert, « ARTFL Encyclopédie : Figure de la Terre », sur artflsrv03.uchicago.edu (consulté le ), p. 6:750
- Mitteleuropäische Gradmessung, General-Bericht über die mitteleuropäische Gradmessung für das Jahr 1865. : Exposé de l'état des Travaux géodesiques poursuivis en Espagne, communiqué a la Commission permanente de la Conférence internationale, par le Colonel Ibáñez, membre de l'Academie Royale des sciences et délégué du Gouvernement espagnol. (Séance du 9 avril 1866), Berlin, Reimer, , 70 p. (lire en ligne), p. 56-58
- Carlos Ibáñez e Ibáñez de Ibero et Carlos Saavedra Menesès (trad. Aimé Laussedat), Expériences faites avec l'appareil à mesurer les bases appartenant à la commission de la carte d'Espagne /: ouvrage publié par ordre de la reine, Paris, J. Dumaine, (lire en ligne)
- Carlos Ibáñez e Ibáñez de Ibero (trad. Aimé Laussedat), Base centrale de la triangulation géodésique d'Espagne / par D. Carlos Ibañez é Ibañez,... D. Frutos Saavedra Meneses,... D. Fernando Monet,... [et al.] ; trad. de l'espagnol, par A. Taussedat,... : Comparaison de la règle géodésique égyptienne avec la règle espagnole, Madrid, (lire en ligne), Appendice N.° 9 p. CXCIII-CCXII
- « BIPM - la définition du mètre », sur www.bipm.org (consulté le )
- (en-US) Charles-Édouard Guillaume, « The Nobel Prize in Physics 1920 : Nobel lecture: Invar and elinvar », sur NobelPrize.org (consulté le ), p. 448
- Ch-Ed Guillaume, « La mesure rapide des bases géodésiques », Journal de Physique Théorique et Appliquée, vol. 5, no 1, , p. 242–263 (ISSN 0368-3893, DOI 10.1051/jphystap:019060050024200, lire en ligne, consulté le )
- Procès-verbaux: Commission Internationale du Mètre. Réunions générales de 1872, Imprim. Nation, (lire en ligne), p. 153-155
- (en) « Dodis - Document - Information », sur dodis.ch (consulté le )
- Comité International des Poids et Mesures, Procès-verbaux des séances de 1875-1876, Paris, Gauthier-Villars, , 134 p. (lire en ligne), p. 3
- (de) « Wild, Heinrich », sur hls-dhs-dss.ch (consulté le )
- Comité International des Poids et Mesures, Procès-verbaux des séances, Deuxième série : Tome II, Session de 1903, Paris, Gauthier-Villars, , 172 p. (lire en ligne), p. 5-7
- Charles-Édouard Guillaume, « Adolphe Hirsch », La Nature, (lire en ligne)
- « Hirsch, Adolphe », sur hls-dhs-dss.ch (consulté le )
- Article 3 de la Convention du Mètre.
- (en) « meter27.jpg », sur NIST (consulté le )
- « Charles-Edouard GUILLAUME (1861-1938) », sur BIPM, (consulté le )
- H. Barrell, The Metre, vol. 3, coll. « Contemporary Physics », , 6e éd. (DOI 10.1080/00107516208217499, Bibcode 1962ConPh...3..415B), p. 415–434
- « Résolution de la 7e CGPM (1927) »
- (en) F. M. III Phelps, « Airy Points of a Meter Bar », American Journal of Physics, vol. 34, no 5, , p. 419–422 (DOI 10.1119/1.1973011, Bibcode 1966AmJPh..34..419P)
- A. A. Michelson et Jean-René Benoît, Détermination expérimentale de la valeur du mètre en longueurs d'onde lumineuses, vol. 11, coll. « Travaux et Mémoires du Bureau international des poids et mesures », , 3e éd., p. 85
- Benoît Jean-René, Charles Fabry et A. Perot, Nouvelle détermination du Mètre en longueurs d'onde lumineuses, vol. 144, Paris, coll. « Comptes rendus hebdomadaires des séances de l'Académie des sciences », (lire en ligne), p. 1082–1086
- Détermination de la valeur en ångströms de la longueur d'onde de la raie rouge du cadmium considérée comme étalon primaire, vol. 2, coll. « Transactions of the International Union for Cooperation in Solar Research », (Bibcode 1908TIUCS...2...17., lire en ligne), p. 18–34
- L. Hollberg, C. W. Oates, G. Wilpers, C. W. Hoyt, Z. W. Barber, S. A. Diddams, W. H. Oskay et J. C. Bergquist, Optical frequency/wavelength references, vol. 38, coll. « Journal of Physics B: Atomic, Molecular and Optical Physics », , 9e éd. (DOI 10.1088/0953-4075/38/9/003, Bibcode 2005JPhB...38S.469H, lire en ligne), S469–S495
- « Nobel Prize in Physics 1907 – Presentation Speech », Fondation Nobel (consulté le )
- K. M. Baird et L. E. Howlett, The International Length Standard, vol. 2, coll. « Applied Optics », , 5e éd. (DOI 10.1364/AO.2.000455, Bibcode 1963ApOpt...2..455B), p. 455–463
- « Résolution 6 de la 11e CGPM (1960) »
- T. H. Maiman, Stimulated optical radiation in ruby, vol. 187, coll. « Nature », , 4736e éd. (DOI 10.1038/187493a0, Bibcode 1960Natur.187..493M), p. 493–494
- K. M. Evenson, J. S. Wells, F. R. Petersen, B. L. Danielson, G. W. Day, R. L. Barger et J. L. Hall, Speed of Light from Direct Frequency and Wavelength Measurements of the Methane-Stabilized Laser, vol. 29, coll. « Physical Review Letters », (DOI 10.1103/PhysRevLett.29.1346, Bibcode 1972PhRvL..29.1346E), p. 1346–1349
- R. L. Barger et J. L. Hall, Wavelength of the 3.39-μm laser-saturated absorption line of methane, vol. 22, coll. « Applied Physics Letters », (DOI 10.1063/1.1654608, Bibcode 1973ApPhL..22..196B), p. 196–199
- K. M. Evenson, G. W. Day, J. S. Wells et L. O. Mullen, Extension of Absolute Frequency Measurements to the cw He☒Ne Laser at 88 THz (3.39 μ), vol. 20, coll. « Applied Physics Letters », (DOI 10.1063/1.1654077, Bibcode 1972ApPhL..20..133E), p. 133–134
- « Résolution 2 de la 15e CGPM (1975) »
- Pollock C. R., D. A. Jennings, F. R. Petersen, J. S. Wells, R. E. Drullinger, E. C. Beaty et K. M. Evenson, Direct frequency measurements of transitions at 520 THz (576 nm) in iodine and 260 THz (1.15 µm) in neon, vol. 8, coll. « Optics Letters », , 3e éd. (DOI 10.1364/OL.8.000133, Bibcode 1983OptL....8..133P), p. 133–135
- D. A. Jennings, C. R. Pollock, F. R. Petersen, R. E. Drullinger, K. M. Evenson, J. S. Wells, J. L. Hall et H. P. Layer, Direct frequency measurement of the I2-stabilized He–Ne 473-THz (633-nm) laser, vol. 8, coll. « Optics Letters », , 3e éd. (DOI 10.1364/OL.8.000136, Bibcode 1983OptL....8..136J), p. 136–138
- « Résolution 1 de la 17e CGPM (1983) »,
- Tom Wilkie, « Time to remeasure the metre », New Scientist, , p. 258–263 (lire en ligne)









