Période radioactive
La période radioactive (ou période quand le contexte ne prête pas à ambiguïté) d'un isotope radioactif est la durée nécessaire pour que la moitié des noyaux de cet isotope initialement présents se désintègrent naturellement. Du point de vue d'un atome isolé, la période radioactive est une propriété probabiliste : c'est la durée à l’issue de laquelle le noyau de l'atome a une chance sur deux de s'être désintégré. Cette propriété ne dépend pratiquement pas[alpha 1] des conditions environnantes (température, pression, champs, etc.), mais uniquement de l'isotope considéré. Le nombre d’atomes d’un isotope radioactif qui se désintègrent naturellement pendant une certaine durée ne dépend donc que du nombre d’atomes initial. La décroissance de ce nombre d’atomes suit une décroissance exponentielle.

La période se mesure en secondes, l'unité de temps du Système international. Les périodes longues sont fréquemment données en années, il s'agit alors (sauf mention contraire) de l'année julienne (1 a = 365,25 jours = 365,25 × 24 × 3 600 = 31 557 600 s exactement[alpha 2]).
Le terme demi-vie[alpha 3] est aussi utilisé, au lieu de période. Il y a débat sur l'usage des deux termes. Pour certains, demi-vie serait plus approprié à la nature du phénomène puisque la radioactivité n'est pas un phénomène périodique. Pour d'autres, période serait plus approprié parce que la décroissance radioactive se répète, identique à elle-même, durant un temps fixé, et que par ailleurs demi-vie peut prêter à confusion (la durée de vie moyenne d'un noyau radioactif n'est pas égale à deux demi-vies[alpha 4], et deux demi-vies ne correspondent pas non plus à la durée de vie du produit).
Dans un contexte médical ou de santé publique, la période radioactive est quelquefois appelée période physique pour la distinguer de la période (ou demi-vie) biologique, qui est le temps au bout duquel la moitié d’une quantité quelconque d’un isotope radioactif a été éliminée de l’organisme, par excrétion aussi bien que par désintégration radioactive.
Période de quelques noyaux radioactifs
La période peut varier considérablement d'un isotope à l'autre, depuis une minuscule fraction de seconde jusqu’à des milliards d'années et même bien davantage. La plus courte demi-vie jamais observée est celle de l'hydrogène 7, (2,3 ± 0,6) × 10−27 s (deux milliardièmes de milliardième de milliardième, ou deux quadrilliardièmes, de seconde), et la plus longue[2] celle du xénon 124, (1,8 ± 0,6) × 1022 a, soit (18 ± 6) trilliards d'années (1 300 milliards de fois l'âge de l'Univers).
La période des radioéléments naturels varie dans de très grandes proportions allant, pour ceux repris dans le tableau ci-dessous, de 3 × 10−7 s (0,3 µs) pour le polonium 212 jusqu'à 1,405 × 1010 ans (14,05 Ga) pour le thorium 232.
| Radioisotope | Notation | Numéro atomique Z |
Abondance relative |
Période radioactive |
Rayonnement émis f−1 |
Produit (* = radioactif) |
|---|---|---|---|---|---|---|
| Rubidium 87 | 87Rb | 37 | 27,835 % | 47 × 109 a | β− | 87Sr |
| Rhénium 187 | 187Re | 75 | 62,6 % | 43,5 × 109 a | α, β− | 183Ta, 187Os |
| Lutécium 176 | 176Lu | 71 | 2,59 % | 37,8 × 109 a | β− | 176Hf |
| Thorium 232 | 232Th | 90 | 100 % | 14,05 × 109 a | α | 228Ra * |
| Uranium 238 | 238U | 92 | 99,28 % | 4,5 × 109 a | α | 234Th * |
| Potassium 40 | 40K | 19 | 0,01167 % | 1,277 × 109 a | β+, β− | 40Ar, 40Ca |
| Uranium 235 | 235U | 92 | 0,718 % | 703,8 × 106 a | α | 231Th * |
| Uranium 234 | 234U | 92 | 0,0056 % | 245,5 × 103 a | α | 230Th * |
| Carbone 14 | 14C | 6 | traces | 5 730 a | β− | 14N |
| Radium 226 | 226Ra | 88 | traces, 100 % | 1 602 a | α | 222Rn * |
| Actinium 227 | 227Ac | 89 | traces, 100 % | 21,773 a | β−, α | 227Th *, 223Fr * |
| Polonium 210 | 210Po | 84 | traces | 138,376 j | α | 206Pb |
| Thorium 234 | 234Th | 90 | traces | 24,1 j | β | 233Pa * |
| Radon 222 | 222Rn | 86 | traces, 100 % | 3,824 j | α | 218Po * |
| Radon 220 | 220Rn | 86 | traces | 54,5 s | α | 216Po * |
| Polonium 216 | 216Po | 84 | traces | 0,158 s | α | 212Pb * |
| Polonium 215 | 215Po | 84 | traces | 1,83 ms | α | 211Tl * |
| Polonium 212 | 212Po | 84 | traces | 0,29 µs | α | 208Pb |
L'activité d’un nombre donné d'atomes d'un isotope radioactif, ou activité spécifique, est inversement proportionnelle à sa période radioactive. Plus un corps radioactif a une longue période (ou demi-vie) plus son activité est faible. Par exemple, le plutonium 239 a une longue demi-vie et une faible activité ; le polonium 210 une faible demi-vie et une forte activité.
Dans le tableau ci-dessous Z désigne le numéro atomique (le nombre de protons du noyau) et A le nombre de masse (la somme du nombre de protons et du nombre de neutrons). Le tableau est initialement classé par ordre de période croissante (d’activité spécifique décroissante).
| Élément | Z | A | Isotope | Période (s, h, j ou a) | Activité spécifique (Bq/mol) | Commentaire |
|---|---|---|---|---|---|---|
| Béryllium | 4 | 8 | 8Be | 6,7 × 10−17 s | 6,23 × 1039 | Exemple de noyau instable, d’existence « fugitive » ; l’activité spécifique indiquée est très théorique car les quelques noyaux éventuellement formés au cours de réactions nucléaires disparaissent quasi instantanément[alpha 5]. |
| 1 s | 4,173 × 1023 | Exemple (théorique) d’un radionucléide dont la période serait égale à une seconde. | ||||
| Molybdène | 42 | 99 | 99Mo | 65,94 h | 1,758 4 × 1018 | Exemple d’isotope très fortement radioactif utilisé dans le domaine médical. |
| Iode | 53 | 131 | 131I | 8,020 7 j | 6,023 × 1017 | |
| Cobalt | 27 | 60 | 60Co | 5,271 4 a | 2,509 × 1015 | |
| Krypton | 36 | 85 | 85Kr | 10,76 a | 1,229 × 1015 | |
| Hydrogène | 1 | 3 | 3H | 12,32 a | 1,073 6 × 1015 | Cet isotope de l’hydrogène est dénommé tritium. |
| Strontium | 38 | 90 | 90Sr | 28,78 a | 4,596 02 × 1014 | |
| Césium | 55 | 137 | 137Cs | 30,07 a | 4,398 85 × 1014 | La période de 31 ans correspond à l’un des principaux seuils de gestion des déchets radioactifs. |
| Américium | 95 | 241 | 241Am | 432,2 a | 3,060 5 × 1013 | |
| Radium | 88 | 226 | 226Ra | 1 602 a | 8,256 8 × 1012 | |
| Carbone | 6 | 14 | 14C | 5 730 a | 2,308 4 × 1012 | |
| Plutonium | 94 | 239 | 239Pu | 24 110 a | 5,486 2 × 1011 | |
| 357 500 a | 3,7 × 1010 | Exemple (théorique) d’un isotope dont l’activité serait égale à un curie par mole (1 Ci/mol). | ||||
| Neptunium | 93 | 237 | 237Np | 2,144 Ma | 6,169 5 × 109 | |
| Iode | 53 | 129 | 129I | 15,7 Ma | 8,425 1 × 108 | |
| Plutonium | 94 | 244 | 244Pu | 80,8 Ma | 1,637 0 × 108 | Le plutonium lui-même a disparu dans la nature, mais les produits de sa décomposition radioactive sont encore détectables et analysables (« radioactivité éteinte »). |
| Uranium | 92 | 235 | 235U | 703,8 Ma | 1,879 4 × 107 | |
| Potassium | 19 | 40 | 40K | 1,248 Ga | 1,059 9 × 107 | 1 Ga (1 milliard d'années) : période au-delà de laquelle on considère comme faible la radioactivité d'un isotope. |
| Uranium | 92 | 238 | 238U | 4,468 8 Ga | 2,959 9 × 106 | Pour mémoire, l'âge de la Terre est estimé à 4,58 Ga, à peine moins que l’âge de formation du Système solaire. |
| Thorium | 90 | 232 | 232Th | 14,05 Ga | 9,414 5 × 105 | Pour mémoire, l'âge de l'univers est estimé à 13,8 Ga (13,8 milliards d'années). |
| Samarium | 62 | 147 | 147Sm | 106 Ga | 1,247 9 × 105 | |
| 1 Ta | 13 230 | 1 Ta (= 1012 a = mille milliards d'années) : période au-delà de laquelle un isotope est considéré comme stable. Il peut donc être en réalité radioactif, mais avec une activité spécifique extrêmement faible. | ||||
| Tellure | 52 | 123 | 123Te | > 10 Ta | < 1 323 | Pour mémoire, 8 000 Bq est l’activité radioactive du corps humain, environ. |
| 1,323 × 1016 a | 1,0 | Corps stable, siège d'une radioactivité infime de 1 Bq/mol. | ||||
| Vanadium | 23 | 50 | 50V | 1,5 × 1017 a | 0,088 18 | Exemple d’un isotope stable dont on a cependant établi la radioactivité (mais extrêmement faible). |
| Bismuth | 83 | 209 | 209Bi | 1,9 × 1019 a | 0,000 696 2 | Exemple d’un isotope stable dont on a récemment mis en évidence la radioactivité (quoique infime). |
Propriété statistique
La période radioactive d'un isotope radioactif est la durée au cours de laquelle son activité radioactive décroît de moitié pour un mode de désintégration donné. Le terme « demi-vie », généralement utilisé, laisse croire que l’activité d'un isotope radioactif est nulle au bout d'un temps égal à 2 demi-vies. En fait, l'activité n'est alors réduite qu'à seulement 25 % de l’activité initiale (voir le tableau de décroissance de l'activité). En réalité, l'activité A vaut, après demi-vies (que soit entier ou pas), , si bien que l'activité n'est jamais mathématiquement nulle.
C'est une propriété statistique : durée à l'issue de laquelle le noyau d'un atome radioactif aurait une chance sur deux de s'être désintégré suivant le mode de désintégration concerné, si ce mode était seul. Cette propriété à l'échelle du noyau atomique ne dépend pas des conditions d'environnement, telles que température, pression, champs, mais uniquement de l'isotope et du mode de désintégration considérés.
La demi-vie peut varier considérablement d'un isotope à l'autre, depuis une fraction de seconde à des millions, voire des milliards d'années.
L'activité d'un nombre donné d'atomes d'un isotope radioactif, après un temps donné, est proportionnelle à ce nombre et inversement proportionnelle à la demi-vie de l'isotope.
Loi de décroissance radioactive
| Nombre de périodes passées | Fraction restante | Pourcentage restant |
|---|---|---|
| % | ||
| 0 | 1 | 100 % |
| 1 | 1/2 | 50 % |
| 2 | 1/4 | 25 % |
| 3 | 1/8 | 12,5 % |
| 4 | 1/16 | 6,25 % |
| 5 | 1/32 | 3,125 % |
| 6 | 1/64 | 1,562 5 % |
| 7 | 1/128 | 0,781 25 % |
| ... | ... | |
| 10 | 1/1 024 | 0,097 656 %[alpha 6] |
| ... | ... | |
| 20 | 1/1 048 576 | ~ 0,000 10 %[alpha 7] |
| ... | ... | |
| 78,995 | 1,660 5 × 10-22 %[alpha 8] | |
| ... | ... |

La décroissance radioactive est un processus de Poisson. La probabilité de désintégration est indépendante du passé et du futur. Pour la dérivation de la loi de probabilité il faut introduire une échelle de temps proportionnelle à la demi-vie. Pour cela on introduit la probabilité cumulative :
- ,
c'est-à-dire la probabilité que la désintégration se produise après un temps t.
Puisque la désintégration est indépendante de l'instant t, U(t) est aussi la probabilité conditionnelle qu'il y ait une désintégration à l'instant t + s sachant qu'il n'y a pas eu de désintégration avant l'instant s, c'est-à-dire : U(t)=U(t + s)/U(s). Ainsi la probabilité cumulative satisfait cette équation :
Dans le cas d'une fonction mesurable l'unique solution est la fonction exponentielle. Soit un ensemble constitué de N éléments dont le nombre décroît avec le temps selon un taux de décroissance noté . L'équation de ce système dynamique (cf. loi de décroissance exponentielle) s'écrit :
où λ est un nombre positif, avec une quantité initiale .
Si on effectue une résolution des équations différentielles à coefficients constants, alors la solution d'une telle équation est la fonction définie par :
Cette fonction décroissante atteint une valeur égale à la moitié de la quantité initiale au bout d'une certaine durée notée . En simplifiant, on obtient alors :
d'où l'on déduit facilement
Cette durée est appelée la demi-vie des éléments de l'ensemble.
Autre formulation simple de l'évolution du nombre de noyaux (N) en fonction du temps :
Remarques
- Il arrive qu'un isotope radioactif comporte plusieurs modes de désintégration, chacun des modes étant caractérisé par une constante radioactive propre λi. La loi de décroissance exponentielle reste valable, et les constantes de désintégration s'ajoutent (λ = λ1 + λ2 + …). La période radioactive reste égale à T = (Log 2)/λ.
- Il arrive aussi qu'un isotope radioactif soit produit en même temps qu'il se désintègre. Le carbone 14 par exemple, radioactif, est produit dans la haute atmosphère par les rayons cosmiques et diffuse vers le sol. C'est aussi le cas des isotopes appartenant à une chaîne de désintégration radioactive (l'isotope radioactif considéré est lui-même le produit de la désintégration de l'isotope en amont dans la chaîne). Dans ces cas, la loi exponentielle simple de décroissance radioactive ne s'applique plus (dans l'expression de dN/dt il y a alors un terme de création en plus du terme de décroissance radioactive).
Sources radioactives usuelles
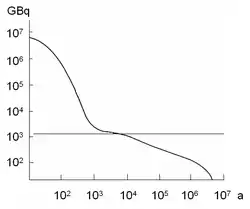
La plupart des sources radioactives contiennent plusieurs et même parfois un grand nombre d’isotopes radioactifs de périodes diverses. Ce cas est courant, puisqu’il est fréquent qu'un produit de désintégration d’un isotope radioactif soit lui-même radioactif. Dans ce cas, la courbe de décroissance de l’activité est assez éloignée d’une fonction exponentielle décroissante, comme le montre la courbe ci-contre.
La notion de période radioactive n’est donc pas pertinente pour caractériser la décroissance radioactive d'une source usuelle telle que du combustible nucléaire usé ou des déchets radioactifs.
Notes et références
Notes
- Pour des phénomènes affectant légèrement la valeur de la période, voir Constante de désintégration#Variabilité de la constante de désintégration. Dans le cas particulier des ions très fortement chargés, voire des noyaux « nus » (sans aucun électron orbital), la période peut être considérablement raccourcie, par exemple d'un facteur un milliard pour le noyau 187Re nu[1].
- L’année grégorienne, elle, compte 31 556 952 secondes, mais il est rare que les périodes soient connues avec une telle précision.
- « Demi-vie » est la traduction littérale de l’anglais half-life, voir l'article en anglais.
- On peut montrer que la durée de vie moyenne d'un noyau radioactif (son espérance de vie) est égale à où désigne la constante de désintégration, donc à et non à : la moitié de l'espérance de vie n'est que d'environ .
- Dans le cœur des géantes rouges, une proportion significative du béryllium 8 ne disparaît pas par désintégration mais par fusion avec un noyau d'hélium 4, ce qui produit du carbone 12, stable.
- Pour dix périodes, la fraction restante est voisine du millième de la quantité initiale. C'est la raison pour laquelle dix périodes est usuellement pris en compte pour déterminer la durée pendant laquelle le confinement des radionucléides doit être assuré. Exemple : un stockage d'un élément de période inférieure à 31 ans doit être conçu pour durer 300 ans.
- Pour une valeur de 20 périodes, la fraction restante est proche d'un millionième de la quantité initiale.
- Pour une valeur proche de 80 périodes, la quantité d'atomes initialement présents a été divisée par le nombre d'Avogadro. Donc sur une mole initiale, il ne reste théoriquement qu'un seul atome. 80 périodes représentent donc un ordre de grandeur de la valeur pour laquelle le corps radioactif a complètement disparu au point, de ne plus pouvoir être détecté au sein des autres corps qui l'entourent par les moyens d'analyse les plus performants imaginables.
Références
- (en) F. Bosch, T. Faestermann, J. Friese, F. Heine, P. Kienle, E. Wefers, K. Zeitelhack, K. Beckert, B. Franzke, O. Klepper, C. Kozhuharov, G. Menzel, R. Moshammer, F. Nolden, H. Reich, B. Schlitt, M. Steck, T. Stöhlker, T. Winkler et K. Takahashi, « Observation of bound-state β− decay of fully ionized 187Re:187Re-187Os Cosmochronometry », Physical Review Letters, vol. 77, no 26, , p. 5190–5193 (PMID 10062738, DOI 10.1103/PhysRevLett.77.5190, Bibcode 1996PhRvL..77.5190B).
- La plus longue demi-vie jamais mesurée est celle du tellure 128, (2,41 ± 0,39) × 1024 a, par désintégration double bêta, mais aucune désintégration n'a jamais été observée : cette demi-vie est déduite de la demi-vie du 130Te et du rapport (connu) des demi-vies de 130Te et 128Te.
Voir aussi
Articles connexes
Liens externes
- Site de l’IRSN (Institut de radioprotection et de sûreté nucléaire) - Glossaire (lien en fin de page)
- Radioactivité : Périodes et activités sur le site de CNRS-IN2P3/EDP-Sciences



















