Notion de poids

Pèse personne publique

La corpulence s'exprime naturellement en termes de poids dans les expressions « perdre du poids » pour dire maigrir, « prendre du poids » pour dire grossir, et le « poids idéal » qui exprime le poids d'une personne présentant une corpulence considérée comme normale.

Les catégories sportives mises en place dans différents sports, permettent de définir un ensemble d'individus pouvant s'affronter à chances, en général physiques, égales dans une compétition. Dans les sports de combat elle principalement basée sur le poids.

Le problème pour les astronautes de la Station spatiale internationale est de se peser en impesanteur.

Bateau volant à vide imaginé par en 1670 Francesco Lana de Terzi, jésuite de Brescia.

La pression exercée par l'eau aux bas du corps étant supérieure à celle exercée sur le haut - on parle de gradient de pression -, il résulte une poussée vers le haut qui s'oppose au poids et qui a tendance à faire remonter le corps vers le haut et le faire flotter. Le Traité des corps flottants, où Archimède énonce les lois de la statique des fluides - et des conditions d'équilibre des corps solides immergés dans un fluide ou flottant sur lui - est probablement la plus connue des œuvres d'Archimède, car tout le monde a présent à l'esprit l'anecdote rapportée par Vitruve suivant laquelle Archimède aurait eu l'intuition du principe fondamental de l'hydrostatique en prenant un bain[13] :

Lorsqu'un corps est plongé en totalité ou en partie dans un fluide pesant en repos les pressions que celui-ci exerce normalement à la surface du corps ont une résultante unique égale et directement apposée au poids du fluide déplacé. Cette résultante étant verticale il en résulte que tout corps plongé en totalité ou en partie dans un fluide en équilibre perd de son poids, le poids du fluide déplacé. Ainsi un corps étant suspendu à un fil il exerce dans le vide sur ce fil une traction égale à son poids, mais si on l'abaisse de manière qu'il vienne plonger dans un liquide, il perd de son poids une portion égale au poids du liquide déplacé, c'est-à-dire que la tension du fil qui le suspend diminue du poids du liquide déplacé. Si le poids du corps est moins grand que celui d'un égal volume du liquide, il s'enfonce jusqu'à ce que le poids du liquide déplacé soit égal au sien, puis il reste flottant et la tension du fil qui le suspendait devient nulle. Si le corps est plus dense que le fluide, il s'immerge complètement et la tension du fil est égale à l'excès du poids du corps sur celui de l'égal volume de liquide[14]. Supposant le fluide homogène en tous ses points, la perte de poids d'un corps entièrement submergé est la même quelle que soit la profondeur à laquelle il se trouve dans le liquide. Ainsi la tension du fil qui le suspend reste constante, et si on coupe le fil, le corps se précipite au fond du vase contenant le liquide et s'y repose en y exerçant une pression verticale égale à la tension du fil, c'est-à-dire égale à la différence entre son poids et celui du liquide déplacé[14]. Ce qui vient d'être dit s'applique à un fluide pesant quelconque. Pour connaître le poids d'un corps il faudrait le peser dans le vide. Si l'on savait combien il pèse dans l'air ou dans tout autre fluide il faudrait ajouter à ce poids celui d'un volume égal de ce fluide pour avoir le véritable poids du corps. C'est sur les principes précédents qu'est fondée la théorie des aréomètres et de la balance hydrostatique.

La poussée d'Archimède s'exerçant pour les gaz, l'homme, pour s'élever dans les airs, a premièrement pensé à se doter d'un énorme ballon rempli d'un gaz plus léger que l'air, variante en quelque sorte de la vessie natatoire des poissons[11]. Les idées de ce genre qui commençaient à se faire jour dès le milieu du XVII^e siècle et anticipée par les jésuites Francesco Lana de Terzi (1631-1687), Bartolomeu Lourenço de Gusmão (1685-1724) et Joseph Galien (en) (1699-1762), sont complètement réalisées par les frères Montgolfier et Jacques Charles en 1782 et 1783.

Winsor McCay. Dream of the Rarebit Fiend episode. 1905

Ed White Gemini 4

L'homme et les animaux se développent et vivent habituellement à la surface de la Terre, c'est-à-dire dans un milieu où la pesanteur a une valeur déterminée relativement uniforme. Pour accroître la pesanteur, il faudrait se rapprocher notablement du centre de la Terre ou se transporter sur une planète de masse plus grande que la Terre ou simuler l'accroissement de pesanteur en créant d'autres accélérations linéaires. Pour diminuer la pesanteur, il faut de même s'éloigner de la Terre ; à une distance suffisamment grande de notre planète, la pesanteur devient très faible, presque nulle, mais un corps ne peut échapper tout à fait à l'influence de l'attraction terrestre que s'il s'approche suffisamment d'un autre astre pour que l'attraction de celui-ci devienne supérieure à celle de la Terre (Point de Lagrange). On peut aussi remplacer l'attraction terrestre par une attraction plus faible en se transportant sur un astre de masse inférieure à celle de la Terre, par exemple sur la Lune. Sur la Terre ou au voisinage de celle-ci, il n'est pas possible de supprimer la pesanteur ; on peut seulement simuler l'impesanteur. Depuis peu de temps est apparue la possibilité pour quelques privilégiés de s'éloigner de la Terre et de vivre, par conséquent, dans des conditions où la pesanteur a une valeur différente.

Lorsqu'un récipient clos contenant divers objets tombe d'un mouvement uniformément accéléré, le contenu et le contenant sont soumis à la même accélération de la pesanteur; par conséquent, le poids des objets qui se trouvent à l'intérieur n'agit pas sur la paroi du récipient, et le contenu se comporte par rapport au contenant comme s'il était sans poids. La chute libre à partir d'une tour élevée est donc un moyen simple de simuler l'absence de pesanteur; mais la résistance de l'air freine la chute et le mouvement rectiligne uniformément accéléré cesse rapidement (Chute avec résistance de l'air); l'impesanteur ne dure que 2 seconde environ.

Une simulation de plus longue durée peut être réalisée en produisant une accélération égale et opposée à celle de la pesanteur, de telle sorte que la résultante des deux forces soit nulle. C'est ce qui a lieu lorsqu'un avion parcourt une trajectoire parabolique dite képlérienne; au cours d'un tel vol, l'avion et ses passagers sont soumis à une force d'inertie centrifuge qui « annule » la pesanteur; la durée d'impesanteur ainsi obtenue ne dépasse pas 45 à 50 s. Quelques minutes d'impesanteur peuvent être obtenues pendant la période dite balistique du vol d'une fusée, période pendant laquelle, la force de propulsion ayant cessé d'agir, la fusée a une trajectoire parabolique. Enfin, et surtout, des périodes d'impesanteur de durée aussi longue qu'on le désire peuvent être réalisées au moyen de vols orbitaux. Un satellite se déplaçant sur une orbite autour de la Terre est en effet soumis simultanément à son poids, qui est centripète, et à une force d'inertie centrifuge de valeur égale; les deux forces se compensant, le satellite est en état d'impesanteur ainsi que les objets et les passagers qu'il contient.

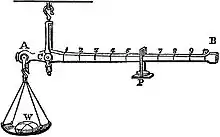
La « romaine » se compose d'un fléau suspendu par une anse qui le divise en deux bras inégaux. Le bras le plus court porte un bassin (appelé « romaine ») ou un crochet (« quintalier ») destiné à soutenir l'objet à peser. L'équilibre est obtenu à l'aide d'un poids constant (curseur) qui, au moyen d'un anneau, glisse sur le bras le plus long : ce seul poids mobile permet de peser divers objets. L'équilibre a lieu lorsque le fléau est horizontal. Si la suspension est établie à l'aide de « couteaux » - appui idéal sur un point que l'on retrouve dans le trébuchet des apothicaires - et qu'on puisse négliger le frottement, on peut dégager l'égalité:

${\displaystyle {\frac {W}{P}}={\frac {CA}{CP}}}$

Avec W, l'objet à peser, C, le point de suspension, CA, la longueur du petit bras et CP, la longueur sur le bras long entre C et le point où le contrepoids P est momentanément suspendu (le bras long porte des divisions équidistantes tracées par le constructeur).

Une balance romaine a toujours deux anneaux de suspension ; on se sert de l'un ou de l'autre selon les cas; pour un produit peu lourd, on suspend l'instrument par celui des anneaux qui permet d'atténuer un peu l'inégalité des longueurs des deux bras. Pour les matières pesantes, on prend, tout au contraire, l'anneau qui accuse cette inégalité. Aussi le bras long d'un bon instrument porte-t-il deux séries de divisions figurant des poids, les uns sous-multiples et les autres multiples d'un même étalon[16].

Partant, par exemple, du principe qu'un rayon plus long se mouvait plus rapidement qu'un rayon plus court sous l'action d'une même force, Thābit ibn Qurra (826-901) considérait que, dans un système mécanique réductible à un levier, le rapport de la force motrice au poids de la chose mue était en raison inverse de leurs vitesses, c'est-à-dire de leurs déplacements circulaires simultanés. Jordanus Nemorarius fait un grand pas en avant lorsqu'il prend en considération non plus des déplacements virtuels le long d'un arc, mais des déplacements verticaux rectilinéaires. Ceci l'amène à l'importante conception de la gravitas secundum situm, la pesanteur selon la situation, c'est-à-dire la composante du poids en fonction de l'obliquité de la descente. Ces vues permettent à Jordanus de déterminer exactement les conditions d'équilibre du levier coudé[17]; elles l'amènent surtout à énoncer correctement, bien avant Simon Stevin (1548-1620) et Galilée, la théorie du plan incliné[18]

Répartition des forces trois poulies.

Les deux moteurs, dit Vitruve, ou puissances qui font agir les machines, différents l'un de l'autre et ne se ressemblent pas; ils concourent pourtant à produire les principes de deux actions: l'une est la force de la ligne droite que les Grecs appellent εὐθεῖα; l'autre, celle de la ligne circulaire qu'ils nomment κυκλωτή. C'est par la suite par des exemples qu'il fait voir que, bien que le mouvement direct soit différent du mouvement circulaire, il n'est pas d'opération mécanique où ces deux mouvements n'agissent ensemble concurremment. Dans la poulie, par exemple, se trouve le mouvement circulaire, et dans la corde qui la fait agir, le mouvement direct. Le levier agit directement, et la main qui l'emploie agit par un mouvement circulaire. Il en est de même des autres machines[19].

Ces machines simples ou complexes sont la poulie (orbiculus ou trochlea) pour laquelle le poids de l'ouvrier ne peut être en dessous de la charge; la première démultiplication apparait avec le treuil (Ou cabestan, vindas, ou sucula en latin) dont l'image nous est rendue par le puits, où la manivelle - plutôt un levier solidaire du tambour -, par la longueur de son bras supérieure au rayon du tambour d'enroulement de la corde, va soulager l'effort de traction au prix d'un parcours plus grand. Ignorant le frottement, la force exercée relativement à la charge dans un treuil peut s'exprimer selon la formule:

${\displaystyle {P}={\frac {L}{r}}{F}}$

Avec ${\displaystyle {P}}$ la charge à soulever, ${\displaystyle {F}}$ la force exercée, ${\displaystyle {L}}$ la longueur de la manivelle et ${\displaystyle {r}}$ le rayon du tambour. Poulie et treuil associés composaient des machines élévatrices, premières chèvres ou grues[20].

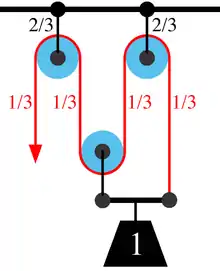
Le palan combine plusieurs poulies (orbiculi) assemblées dans des moufles par lesquelles le câble de traction avec une puissance qui sera proportionnelle au nombre de poulies:

${\displaystyle {F}={\frac {P}{2}}}$ pour deux poulies; ${\displaystyle {F}={\frac {P}{n}}}$ pour n poulies.

Un supplément de puissance était assuré par de grandes roues (majus tympanum) - substitut à la poulie - dans laquelle pouvaient courir des hommes, dispositif qui prendra le nom de roue de carrier ou de cage d'écureuil.

Les penseurs antérieurs au XVII^e siècle développent le concept de poids inhérent au corps, avec peut-être l'arrière-pensée animiste que le corps pesant « tend » vers le bas parce qu'il veut tomber; les mouvements qui s'effectuent sur Terre sont rectilignes finis et imparfaits, comme l'est de façon générale le monde sublunaire. Au contraire, le monde supralunaire, celui de l'éther « inengendré, indestructible, exempt de croissance et d'altération », est celui du mouvement circulaire, éternel.

Pour Aristote, l'univers est constitué par huit sphères concentriques, emboitées l'une dans l'autre, autour de la terre immobile, leur centre commun. Les corps terrestres, formés par la combinaison des quatre essences, soumis à la génération et à la corruption, ont une autre nature et sont soumis à d'autres lois que les corps célestes: une cinquième essence forme ceux-ci, les dieux véritables, les anime sans fin d'un mouvement circulaire, écarte d'eux à jamais la corruption et la mort. Le monde sublunaire, enfin, est entièrement régi par les mouvements des corps célestes: comme ces mouvements sont uniformes et circulaires, il suit que l'avenir est prévisible par l'astrologie et que l'histoire humaine se répète sans fin[21]. Aristote (-384, -322) résout la question du mouvement en affirmant que tout mouvement d'un corps résulte de la tendance de celui-ci à rejoindre son lieu naturel - ce qui explique que la fumée monte vers le ciel et qu'une pierre jetée en l'air, retombe vers la terre[22].

Aristote induit un univers fini, en dehors duquel il n'y a pas d'espace vide (ruinant les fondements de la géométrie euclidienne, qui comportait l'infinitude de certains éléments), une distinction artificielle entre des mouvements naturels et des mouvements forcés, tout cela par un choix peu heureux d'exemples de mouvements qu'il croit simples alors qu'ils sont très complexes; les siècles qui suivront, vouant à Aristote une foi aveugle dans sa supériorité sur tous les autres représentants du génie grec[23] engageront la science dans une impasse qui durera deux mille ans. Relayée par la scolastique médiévale, certains principes de mécanique survivront jusqu'au XVII^e siècle.

La révolution scientifique, qui détermine le cours de la physique moderne, s'accomplit lentement, elle est le fait de penseurs qui s’opposent à la science aristotélicienne. Quoi que veuille Aristote, il ne semble pas y avoir de différence essentielle entre la substance du ciel et celle de la terre: Platon, saint Augustin et saint Anselme l'ont deviné; les disciples de Scot ont raison de poser ici et là une matière de même nature. Jean Buridan (1292 - 1363) ose même déclarer que les mouvements célestes et les mouvements terrestres sont régis par les mêmes lois. Albert de saxe (v. 1316-1390), son disciple, reprenant une idée péripatéticienne, voit dans la pesanteur une manière de désir, inhérent au corps, et qui le pousse au centre du monde. D'où il déduit même cette conséquence curieuse: la terre se meut, puisque son centre de gravité « désire » constamment se placer au centre du monde et que, de par l'érosion creusant les vallées et comblant les mers, la position de ce centre de gravité varie sans cesse[21]. Idée rejetée par Jean Buridan. Le mouvement des astres, enseigne-t-il, « ne s'explique pas par l'action des âmes qui leur sont unies; c'est celui que Dieu leur a imprimé à la création du monde en les animant d'une force », impetus, qui continue à les mouvoir. Voilà donc brisé le prestige divin des astres que la science aristotélicienne avait consacré[21]. Jean Buridan reprend les idées anciennes de Jean Philopon, commentateur d'Aristote au VI^e siècle, et explique le mouvement, non plus par le contact entre un moteur et un mobile, mais par la possibilité pour le mouvement de conserver en lui un certain élan que le moteur assure au corps mû, et qu'il qualifie d'Impetus. C'est la diminution de la force de l'impetus qui expliquerait la chute des corps. Cette théorie du mouvement est encore présente dans la première forme de pensée de Galilée (notamment dans son De motu); elle constitue un premier pas vers l'instauration du principe d'inertie. Disciple de Buridan, Albert de Saxe applique la théorie de l'impetus aux orbes célestes et propose une nouvelle théorie de la « gravité » qui distingue entre la gravité d'un corps et celle de la Terre, provoquant un long débat auquel prendront part encore Léonard de Vinci, Girolamo Cardano et Bernard Palissy[24]. Albert de Saxe crée d'un coup la cinématique[21]. Les docteurs scotistes, ses émules, y ajoutent une théorie du mouvement, etc.

Au Moyen Âge, par les travaux des écoles d'Oxford (les calculateurs d'Oxford) et de l'université de Paris (Nicole Oresme), l'estimation des vitesses fait incontestablement de grands progrès grâce à la conceptualisation de la vitesse comme grandeur intensive (Théorème de vitesse moyenne) et à la précision qui s'ensuit pour l'idée de variation de vitesse[25]. Galilée et Descartes établiront la position prépondérante des mathématiques. Avec Galilée l'état de mouvement d'un corps soustrait à toute force est reconnu comme celui d'un mouvement rectiligne et uniforme, introduction au principe d'inertie sur lequel Isaac Newton viendra fonder la mécanique moderne[23].

Horloge à gravité

Aristote suppose qu'un mobile dix fois plus lourd qu'un autre se mouvra dix fois plus vite et tombera dès lors deux fois plus rapidement. Toujours de manière erronée il s'insurge contre certains anciens qui introduisirent le vide comme nécessaire au mouvement, en disant que sans celui-ci, le mouvement ne pourrait avoir lieu. Déduisant de la difficulté qu'un mobile éprouve à se mouvoir dans un milieu dense - il postule que la vitesse dans l'air par rapport à la vitesse dans l'eau est dans le rapport inverse de densité de l'un, par rapport à la densité de l'autre. Si le vide pouvait exister, le mouvement se ferait en un instant, ce qui est impossible. Par conséquent en vertu de l'existence du mouvement, il est impossible qu'il y ait du vide. Tout corps grave qui tombe possède selon Aristote une certaine vitesse, déterminée par la nature, et que l'on ne peut ni accroître ni diminuer, si ce n'est en usant de la violence ou en lui opposant une résistance[26]. Toutes ces assertions sont battues en brèches par Galilée.

La loi de la chute des corps professée par Galilée dans son De Motu, qui sonne le glas de la physique aristotélicienne, comporte deux assertions qui, bien qu'étroitement liées dans l'esprit de Galilée, peuvent être distinguées de cette manière: La première affirme que ce mouvement obéit à la loi du nombre et que les espaces traversés dans des intervalles successifs (et égaux) du temps sont ut numeri impares ab unitate: Dans le mouvement de la chute, les vitesses croissent proportionnellement au temps comme les nombres, les espaces parcourus dans les intervalles successifs, comme les nombres impairs, et les espaces parcourus depuis le commencement de la chute, comme les carrés. En d'autres termes, à l'encontre de ce qu'avait enseigné Aristote, une force détermine non pas un mouvement uniforme, mais un mouvement uniformément accéléré, et l'action de la force motrice produit non pas une vitesse, mais une accélération. La deuxième ajoute que dans leur mouvement de chute, également à l'encontre d'Aristote, tous les corps, grands et petits, lourds et légers, c'est-à-dire quelles que soient leurs dimensions et leurs natures, tombent, en principe, sinon en fait (Pour que l'assertion soit vérifiée de manière complète, elle doit être réalisée dans le vide), avec la même vitesse; Pour Galilée qui n'admet pas d'attraction terrestre comme le fera Newton, l'accélération de la chute est une constante universelle[26].

Ce qu'a montré Galilée, c'est que la force d'inertie (qui est fonction de la masse) compense exactement le poids de l'objet (lui aussi fonction de la masse): un objet plus lourd devrait tomber plus vite, mais comme il est plus difficile à mettre en mouvement, il tombe à la même vitesse qu'un objet plus léger. La formule qui lie la vitesse d'un corps en chute libre à la gravité, que l'on retrouve dans la formule de Torricelli ${\displaystyle v^{2}=2\,g\,h}$, ne fait donc pas intervenir le poids. La masse d'un corps physique renvoie donc à deux natures phénoménologiques distinctes: La masse grave est la propriété de la matière qui se manifeste par l'attraction universelle des corps, et au quotidien, par leur poids et la masse inerte, la propriété de la matière qui se manifeste par l'inertie des corps.

L'expérience réalisée par Galilée selon la légende du haut de la tour de Pise est renouvelée par Apollo 15 dans atmosphère insignifiante de la Lune.

Le terme poids s'utilise pour désigner les morceaux de cuivre, de plomb, de fer et de pierre, qui sont attachés aux cordes d'une horloge mécanique, d'un tournebroche, pour lui donner du mouvement, en régler le mouvement. L'inconvénient de donner aux horloges un nouveau moteur en se servant de la pesanteur des corps solides est que ces corps, comme l'eau, s'accélèrent dans la chute et tombent donc plus vite à la fin de leur descente qu'au commencement. L'échappement entraîné par le balancier a comme but de retarder continuellement la descente du poids et ainsi de détruire l'accélération afin de ne laisser au poids dans tous les moments de sa chute que la vitesse uniforme qu'il a dans le premier instant. Le mouvement n'est plus accéléré et devient uniforme, ce qui est le principe de la régularité des horloges[27].

Un contrepoids est une masse inerte utilisée pour contrebalancer le poids de la charge dans un mécanisme de levage. Disposé à l'extrémité opposée de la charge à soulever, dans un système à levier ou à poulie, le contrepoids facilite la manœuvre des charges lourdes.

Les expressions « c'est une affaire de poids », « peser sur les relations », le « poids des mots », etc. reprennent cette partie active qu'a le poids dans le mécanisme.

Le Baron de Münchhausen sur un boulet de canon

Les expériences réelles sont, souvent, très difficiles à faire, impliquent éventuellement un appareillage complexe et coûteux, comportent, nécessairement, un certain degré d'imprécision et donc, d'incertitude. Il est impossible, en effet, de produire une surface plane ou sphériques qui le soient véritablement. Il n'y a pas, et il ne peut pas y avoir, in rerum nátura, de corps parfaitement rigides pas plus que de corps parfaitement élastiques; on ne peut pas exécuter une mesure parfaitement exacte. « La perfection n'est pas de ce monde; on peut s'en approcher, sans doute, mais on ne peut pas l'atteindre. » Entre la donnée empirique et l'objet théorique, il reste, et il restera toujours, une distance impossible à franchir. C'est là que l'imagination entre en scène. Allègrement, elle supprime l'écart. Elle ne s'embarrasse pas des limitations qu'impose le réel. Elle « réalise » l'idéal, et même l'impossible. Elle opère avec des objets théoriquement parfaits, et ce sont ces objets-là que l'expérience imaginaire met en jeu, Ce qu'Ernst Mach appellera « Expérience de pensée »[26].

Le mécanicien manipule des billes, pour établir les lois du mouvement. La forme pleine, dense et parfaite des boulets de canon ne pouvait le laisser indifférent[28], comme par ailleurs le troufion qui pour tromper l'ennui initia au XVII^e siècle, le lancer de boulets de canon qui fait partie des derniers développements de la discipline sportive du lancer du poids[29]. Entre autres curiosités martiales, le Skalenpfund (de) d’artillerie, unité de poids russe fait référence au poids d'un boulet de canon de fonte de 2 pouces russes de diamètre à une température de 13 1/3 Réaumur. Sa masse était de 489,163 7 grammes.

Le canon même longtemps après l'époque de sa découverte semble avoir été considéré avec une sorte de terreur mystérieuse. La ligne invisible parcourue par ses projectiles était regardée comme différant complètement de celle suivie par les autres projectiles et les blessures faites par les armes à feu en général étaient toutes regardées comme nécessairement mortelles[30] - [31].

Le mouvement des projectiles qui se déplacent le long d'une trajectoire courbe (aussi différente que la ligne droite vers le centre de la Terre qu'ils devraient suivre selon leur inclination naturelle, en accord avec la physique aristotélicienne) est, au Moyen Âge, le problème standard de mouvement violent. Tous les philosophes conviennent en accord avec Aristote que lorsque le mouvement est violent, la force n'est pas causée par la nature ou la «forme substantielle» du corps[32]. La détermination de l'origine de cette force devient particulièrement importante au XIV^e siècle, avec l'utilisation croissante de l'artillerie dans les combats.

Au XIV^e siècle, la théorie aristotélicienne est largement critiquée[32]. De manière prosaïque, dire qu'un boulet de canon rejoint son lieu naturel ne permet pas de mesurer avec la précision désormais nécessaire, la distance entre le canon et le point de chute[30]. Guillaume d'Ockham (1285 - 1347) argumente en citant le cas de deux flèches volant l'une vers l'autre, mais dans des directions opposées. Si leurs mouvements est explicable comme un effet du milieu environnant, l'air doit être considéré comme ayant une force motrice dans deux directions opposées à la fois, ce qui est absurde. Ockham convient donc à un moment donné de l'hypothèse selon laquelle la force sur la flèche vient directement de l'arc, sans que le médium ne joue de rôle. Il semble qu'il soit le seul philosophe médiéval à considérer l'action à distance comme principe de la mécanique, mais même plus tard, il abandonne cette hypothèse et a adhère à l'axiome philosophique général qu'aucun agent ne peut avoir d'effet à distance. Ockam se contente, en troisième lieu, de déclarer qu'un corps se déplace simplement parce qu'il se déplace. En d'autres termes: pour expliquer le mouvement, il n'est pas nécessaire d'assumer une force de déplacement. À ce moment, Ockam n'a pas de partisans parmi les philosophes médiévaux. Ses contemporains adhèrent indubitablement au dogme selon lequel la force et le mouvement sont inséparables. Les philosophes de théorie de l'Impetus du XIV^e siècle rejettent ces trois doctrines et se réfugient dans une quatrième hypothèse, la théorie dite « impetus » qui a son origine dans l'œuvre de Jean Philopon. Aux XII^e siècle et XIII^e siècle, la théorie de l'impetus se trouve quelquefois dans les écrits des savants latins, mais elle a peu de partisans. Au XVI^e siècle, la théorie de l'impetus est généralement acceptée et, vers 1320, enseignée à l'Université de Paris[32].

Balistique. Walther Hermann Ryff. 1547. Hypothèse de trajectoire des boulets alors en usage

Walther Hermann Ryff. 1547. Mesure de l'angle du canon au fil à plomb

Jean Buridan (1292 et 1363) va plus loin et précise cette thèse en expliquant que le corps dense, parce qu'il contient plus de matière relativement a son faible volume, peut expliquer pourquoi tel corps peut être lancé plus loin qu'un autre corps. Replacé dans le contexte de la physique classique il s'agit du premier élément de la théorie de la quantité de mouvement ${\displaystyle p=m.v}$ que défendra plus tard Descartes[24] toutefois replacé dans le contexte de la théorie dynamique de l'impetus, il joue un rôle différent[32].

Jean Buridan débat du mouvement violent en se référant notamment aux « machines qui projettent de grandes pierres », sans préciser s'il s'agit des canons ou des antiques catapultes. Le problème de la force de déplacement d'un projectile est alors abordé de plusieurs façons. Tout d'abord, la théorie aristotélicienne traditionnelle suppose que la force agissant sur le projectile provient directement de l'air environnant qui, à son tour, l'a reçu de la catapulte. À un certain point, la force est épuisée et le projectile tombe à terre. Le résultat de cette théorie est que le chemin du projectile (la courbe balistique) est composé de deux lignes droites; Le projectile se déplace vers le haut dans une direction déterminée par l'angle de la catapulte ou du canon, puis soudainement verticalement vers le bas. L'utilisation occasionnelle de cette hypothèse peut être vue en artillerie[32].

Thomas d'Aquin réfute la théorie de l'impetus à plusieurs reprises, mais l'utilise dans son explication de la façon dont une balle rebondit quand elle est empêchée par mur solide. La raison donnée par d'Aquin est que la main qui lance une balle lui a donné une certaine impulsion de mouvement. Cette impulsion est conservée pendant l'impact, et est donc capable de porter la balle loin du mur[32].

Le mathématicien italien Niccolo Fontana Tartaglia (1499-1557) est le premier qui applique le raisonnement mathématique au tir de l'artillerie. Il se donne beaucoup de peine pour démontrer qu'aucune partie de la trajectoire d'un boulet de canon n'est en ligne droite, mais qu'il décrit une courbe dès l'origine de son mouvement hors de la bouche; il prouve de plus qu'un canon tire le plus loin possible sous l'angle de 45°. Dans son Nova scientia de 1550, Tartaglia commence par décrire un instrument pour mesurer l'angle que forme le tube avec l'horizontale. Il s'agit d'une équerre dont on introduit un côté dans la bouche de l'arme et au sommet de laquelle est fixé un fil à plomb. Un quadrant gradué est également fixé à l'équerre, et l'on peut donc mesurer l'angle que forme le fil à plomb avec l'horizontale[30].

Tartaglia passe encore pour avoir découvert le quart de cercle des canonniers.

La notion d'impetus proclamée en prolongement de la physique d'Aristote disparaîtra au cours du XVII^e siècle pour céder place à celle d'inertie professée par Galilée.

Il est réservé à Galilée et à son élève Toricelli de serrer de plus près les lois de la chute des corps. Tartaglia prouve qu'un boulet au sortir du canon se meut suivant une courbe, Galilée démontre que cette courbe est une parabole pourvu que le point de chute du boulet soit dans le même plan que la batterie d'où il a été tiré et que la pièce soit élevée au-dessus de l'horizon; il prouve de plus que c'est une moitié de parabole quand le canon dans les mêmes circonstances est pointé horizontalement. Evangelista Torricelli étend ces découvertes, il montre que le boulet, soit qu'il tombât au-dessus ou au-dessous du plan où se trouve son point de départ, décrit une parabole d'une plus ou moins grande amplitude suivant l'angle sous lequel le canon est pointé et suivant la force de la poudre. C'est Jean-Baptiste Baliani, disciple de Galilée, qui énonce et généralise l'inertie comme loi fondamentale du mouvement, énoncée comme suit:

« Tout corps persévère dans son état de repos ou de mouvement uniforme en ligne droite, à moins qu'il ne soit contraint, par des forces s'imprimant sur lui, à changer cet état. »

Avant l'époque de Galilée, le tir de l'artillerie était défectueux parce qu'on n'y appliquait pas la science mathématique; après ce physicien le tir est défectueux surtout parce que ses théories sont trop exclusivement adoptées et qu'on ne tient pas suffisamment compte des causes d'erreur accidentelles, parmi celles-ci le frottement de l'air.

Habitués à nous mouvoir doucement comme nous le faisons à travers l'atmosphère qui se divise devant nous et se referme quand nous avons passé si bien qu'il est devenu le véritable type d'un milieu non résistant, c'est à peine si nous pouvons bien apprécier l'immense résistance qu'il oppose à un projectile animé d'une grande vitesse. Les expériences de Galilée furent faites sur des corps se mouvant lentement, sur lesquels la résistance de l'air ne pouvait avoir qu'une faible influence, de sorte que leur trajectoire parabolique n'aura été que légèrement déformée, et qu'il n'aura pas apprécié à sa juste valeur l'influence due à cette cause. Cependant Galilée n'ignorait pas que l'air oppose en effet une certaine résistance, mais il crut qu elle était plus négligeable qu'elle ne l'est réellement. Les idées de Galilée furent adoptées à peu près universellement. Edmond Halley en 1686 affirma d'une manière positive que pour les gros projectiles métalliques dont le poids surpasse d'un grand nombre de fois celui d'un pareil volume d'air, et dont la force est très grande relativement à la surface sur laquelle l'air presse, sa résistance est à peine sensible et il conclut du résultat de l'observation, que si pour un petit projectile léger on peut et on doit tenir compte de la résistance de l'air, dans le tir des grosses et lourdes bombes on peut y faire peu ou point attention[33].

Les artilleurs auraient pu être amenés à douter de la vérité de cette assertion du docteur Halley par l'autorité d'un plus grand nom, Isaac Newton qui en 1687 démontre que la courbe décrite par un projectile dans un milieu fortement résistant diffère de la parabole et que la résistance de l'air est assez grande pour produire entre la courbe de projection d'un corps pesant et une parabole une différence sensible et trop considérable pour être négligée. Christian Huygens en 1690 énonce les mêmes principes. Malgré le témoignage de deux pareils hommes, et un témoignage encore meilleur celui de la pratique, l'erreur de Galilée continue à se propager. On peut se demander comment il se fait que les erreurs de la théorie parabolique se perpétuent lorsqu'il est alors si facile par la pratique de les démontrer. La réponse c'est que beaucoup sont paralysés par le grand nom de Galilée et n'osent pas se hasarder à penser par eux-mêmes; beaucoup attribuent le manque de concordance existant entre la théorie et la pratique à l'intervention de quelque cause; à toute chose excepté à la vraie L'incertitude demeura jusqu'en 1742, année où Benjamin Robins publie son traité appelé « New Principles of Gunnery » qui prend pleinement considération du frottement de l'air. Les principes développés dans ce traité sont bientôt après confirmés par Leonhard Euler et largement appliqués par la balistique moderne[33].

Canon de Newton

Le canon de Newton est une expérience de pensée utilisée par celui-ci pour énoncer sa conjecture selon laquelle la gravitation est la composante majeure du poids (ou force de pesanteur). Pour expliquer comment un corps peut orbiter un autre, Newton demande à ses lecteurs d'imaginer un canon au-dessus d'une très haute montagne imaginaire. Le canon est chargé de poudre et tire. La balle de canon suit une courbe balistique, tombant de plus en plus vite en raison de la gravité de la Terre et frappe la Terre à une certaine distance. Qu'on utilise plus de poudre à canon et voici ce qui peut se produire (Les quantités de poudre à canon sont simplement imaginaires, ne doivent pas être précises! En outre, l'expérience ignore le fait que l'air entraîne une traînée sur le boulet et la ralentit.):

• 2 sacs de poudre: Le boulet va très vite et très loin avant que la gravité ne le ramène à Terre.
• 3 sacs de poudre: Le boulet part en orbite et tombe très loin de l'autre côté de la terre.
• 4 sacs de poudre: Le boulet orbite de manière complète autour de la terre et ne redescend plus.
• 5 sacs de poudre: Le boulet va si vite qu'il échappe complètement à la gravité de la Terre.

La même chose se produit lorsqu'une navette spatiale ou un satellite sont lancés en orbite. La fusée spatiale élève le vaisseau spatial à la hauteur de cette « montagne très haute » et communique également au vaisseau spatial ce que l'on appelle sa vitesse de satellisation minimale, comme la poudre à canon la communique au boulet. Ainsi, l'engin spatial tombe tout autour de la Terre, mais ne frappe jamais sa surface. La courbure du chemin du vaisseau spatial est à peu près la même que la courbure de la surface de la Terre. Ainsi, les astronautes qui orbitent autour de la Terre ne sont pas vraiment sans poids, ils tombent simplement et tombent encore en chute libre[34].

Le poids d'un corps, relevant a priori d'une action extérieure, ne peut plus servir de grandeur constante servant à caractériser le corps, à exprimer une idée de quantité de matière. Le marchand peut continuer de s'en servir à cette fin; mais pas le philosophe, du moins pas sans précaution; c'est pourquoi il lui a fallu inventer la masse. Le poids est conçu, plus précisément, comme force motrice imprimée par la gravité; autrement dit comme manifestation d'une hypothétique action de la Terre sur le corps. Au début, on est censé ne connaître que celle que la Terre exerce ; au bout du compte, tout corps l'exerce sur tout autre[1].

Le poids d'un corps est le produit de sa masse par l'accélération due à la pesanteur (${\displaystyle g}$) dans le lieu où l'on se trouve de sorte que le poids (${\displaystyle p}$) représenté par le produit ${\displaystyle m.g}$ représente tout aussi bien une force. C'est même la seule manière d'introduire dans les considérations de la mécanique l'idée d'une force constante. On la figure partout en imaginant un poids qui agit dans une direction donnée et dont la valeur est représentée par une longueur comptée sur la ligne suivant laquelle s'exerce son action. La masse qui représente la quantité de matière est absolument indépendante du poids et de l'accélération due à la pesanteur car la fraction ${\displaystyle p/g}$ qui en donne la valeur est constante, le poids variant de la même manière que l'accélération. Ce qui explique, par exemple, l'effroyable destructivité des accidents de la route. Masse et énergie deviennent des idées interchangeables. C'est, dit Bachelard, un « rationalisme complet ».

Si au moyen d'un ressort ou dynamomètre on pèse un litre d'eau distillée à 1 degré au pôle à l'équateur et sur un point quelconque pris sur un méridien on verra que le poids de cette même masse d'eau varie de manière à prendre une valeur maximum au pôle, une valeur minimum à l'équateur et des valeurs décroissant régulièrement du pôle à l'équateur (Gravimétrie). Mais le poids diminue dans le même rapport que l'accélération en augmentation de la vitesse de chute par seconde, de sorte que le rapport ${\displaystyle p/g}$ reste constant comme la masse que ce rapport représente. Aussi pour nous une force constante pourra toujours être représentée par un poids.

Les valeurs relatives des poids ou des forces nous sont données par l'action qu'ils exercent sur des balances ou dynamomètres. Mais la notion première du poids est toujours corrélative de la pression qu'un corps exerce sur notre main, quand celle-ci s'interpose entre la terre et lui. Les mots force, poussée, résistance, répondent toujours à la sensation qu'éprouvent nos organes dans le cas où ils en reçoivent une pression qui est d'autant plus intense que la masse et l'accélération sont elles-mêmes plus grandes. Ainsi un litre d'eau comprime plus la main d'un observateur qui serait placé au pôle que s'il était transporté à l'équateur. On peut dire que cette pression est proportionnelle à la masse du corps et à l'accélération qu'il prend en tombant en chaque lien vers la terre.

Lorsqu'un homme soulève un poids p et le transporte à une hauteur verticale ${\displaystyle h}$ on dit qu'il a produit un travail égal au produit ${\displaystyle p.h}$, au poids multiplié par son déplacement vertical; c'est l'effet produit par l'action qu'il exerce sur la matière pour la mettre en mouvement. En général si un mobile possédant une masse m et animé d'un mouvement dont l'accélération est ${\displaystyle g}$, parcourt un espace h mesuré sur la direction que prend naturellement le mobile, quand aucun obstacle ne change cette direction, le produit ${\displaystyle m.g.h}$ représente le travail qu'accomplit alors le mobile. Il faut remarquer que ${\displaystyle g}$ et ${\displaystyle h}$ représentent ici des longueurs exprimées en mètres par exemple et que le travail peut être dès lors considéré comme le produit d'une surface par la masse.

La première édition des Principia de Newton se terminait abruptement sur les trajectoires des comètes, mais la deuxième édition de 1713 ajoutait un Scolie Général qui était une confession religieuse et aussi un aveu d'échec: « causam gravitatis nondum assignavi », « je n'ai pas encore assigné les causes. » Après Newton, on a échoué à trouver le mécanisme qui aurait rendu compte de la gravité. Ceux qui viendront après lui chercheront à leur tour, et souvent se décourageront, et se contenteront des résultats du calcul et il s'instaura peu à peu une nouvelle "philosophie naturelle", assez pauvrement philosophique à vrai dire, où le traitement mathématique des forces et des mouvements prit définitivement le pas sur les explications causales. Une forme nouvelle de science de la nature naissait ainsi, incurieuse et satisfaite de la superficialité mathématique[35]. Le poids d'un corps est resté, pour l'essentiel, une manifestation de la mystérieuse attraction universelle. De nos jours, en physique théorique, on ne se sert plus de « poids » pour désigner un corps pesant. Le mot désigne une force, et même une force partiellement fictive s'exerçant sur le corps, ainsi que la valeur de celle-ci. Et tandis que « gravitation » tente de résister à la concurrence ď « attraction », « graviter » en est venu à signifier « tourner autour ». On en oublierait que, du fait du principe d'inertie, un astre ne fait ses révolutions qu'en tombant[1].

Sphère de silicium de 93,6 mm de diamètre proposée comme définition du kilogramme

La première idée de la commission royale instituée par Louis XVI chargée de composer un nouveau système d'unités était de créer une unité de masse qui porterait le nom de « grave ». Dans le nouveau système métrique la classe monétaire dérive des poids, celle des poids dérive de celle des mesures de capacité, les mesures de capacité et de superficie dérivent des mesures linéaires, les mesures linéaires dérivent du mètre, et le mètre de la longueur du quart du méridien terrestre. Le litre étant la mesure de capacité équivalant à un décimètre cube (équivalant à la pinte), le grave équivaudrait à la masse d'un litre d'eau à la température de congélation, c'est-à-dire pratiquement 1 kg et serait représenté par un étalon de masse. Après la Révolution, le nouveau Gouvernement républicain reprend l'idée du système métrique, mais décide du « gramme » comme unité de masse (Gramme est le nom grec du poids que les Romains nommaient scrupule ou scripule propre à servir d'unité dans les pesées des matières précieuses telles que l'or, etc.). Comme le kilogramme, poids de mille grammes est le plus commode pour la vente des marchandises les plus communes, on l'a adopté pour unité principale des poids, il équivaut au poids de l'eau sous le volume d'un décimètre cube (ce qui répond à 2 livres 5 gros 35 grains. 15/100 ancien poids de marc[36]). Un étalon d'un gramme étant aussi difficile à utiliser qu'à établir, décida à représenter l'unité de masse par un étalon d'un kilogramme[37]. Longtemps l'établissement du kilogramme a été vu comme un objet d'entraves pour le commerce et certains trouvaient dans son usage de telles difficultés qu'ils ne se mirent jamais au « nouveau Poids ». Les Fabriques de soie surtout ne pouvant s'en servir dans toutes leurs opérations le jugeaient même impraticable[38].

On a longtemps hésité à affecter le kilogramme à la mesure de la masse, ou à celle du poids. Dans le commerce et dans l'usage journalier, les masses étalonnées représentant les fractions et les multiples du kilogramme portent le nom de poids, et l'on ne juge pas prudent de rompre avec une dénomination consacrée par une tradition remontant à plusieurs siècles. La loi autrichienne au XIX^e siècle par exemple porte que les représentants matériels du kilogramme et de ses multiples ou sous-multiples conservent dans l'usage journalier et dans le commerce la dénomination poids[39].

Une unité de force déjà nettement définie et dénommée était la dyne, créée au milieu du XIX^e siècle par l'Association britannique, et remplacée dans les sciences appliquées, à cause de sa petite valeur absolue, par son multiple la mégadyne. La dyne, du grec ancien δύναμις, est la force qui agissant sur un gramme de matière pour une seconde génère une vitesse de centimètre par seconde. La mégadyne avait cet avantage qu'elle ne contenait aucun coefficient arbitraire, tandis que l'unité kilogramme-force que la troisième Conférence générale des poids et mesures de 1901 institue comme unité de poids contient explicitement un tel coefficient : La 3^e CGPM institue le kilogramme comme unité de masse ; il est égal à la masse du prototype international du kilogramme conservé dans les coffres-forts du Service international des poids et mesures ; Le terme « poids » désigne une grandeur de la même nature qu'une force; le poids d'un corps est le produit de la masse de ce corps par l'accélération de la pesanteur; Le nombre adopté dans le SIPM pour la valeur de l'accélération normale de la pesanteur est alors de 980,665 cm/s2, nombre sanctionné déjà par quelques législations. L'unité de force porte donc la même dénomination que l'unité de masse quoique les deux conceptions soient totalement différentes.

L'usage du newton comme unité de force est rendu obligatoire à partir de 1948, lors de la quatrième séance de la neuvième Conférence générale des poids et mesures[40]. La 9^e CGPM établit d'autre-part le joule, comme le travail produit par un newton, dont le point d'application se déplace de un mètre dans la direction de la force (le watt, la puissance qui produit 1 joule par seconde). Le pascal, la pression qui s'exerçant uniformément sur une surface de 1 mètre carré produit une force de 1 newton; et d'autres unités comme la décapoise, unité de viscosité dynamique ou la myriastokes, unité de viscosité cinématique. L'introduction du newton rend obsolète le kilogramme-force.

Dans le Système international d'unités, la masse s'exprime en kilogrammes et la force comme le poids s'expriment en newtons, équivalant au kilogramme-mètre par seconde carrée (kg m/s²). Un newton est la force capable de communiquer à une masse de 1 kilogramme une accélération de 1 m/s².

L'accélération ${\displaystyle g}$ s'exprime en m/s2 et vaut de manière conventionnelle: 9,806 65 m·s^-2.

Dans les unités de mesure anglo-saxonnes la masse s'exprime en livre-masse (lb) et le poids en livre-force. La livre-force est utilisée et strictement équivalente au poids exercé par la force de gravitation terrestre sur une masse d'une livre-masse. D'où une facilité d'appréhension mais également, une possible source de confusion entre les deux unités.

La discipline qui traite des machines va prendre le nom de mécanique. Selon Aristote, la μηχανή (mèkané) est la partie de la technique qui vient à notre secours chaque fois qu'il faut faire quelque chose contre la nature, et que l'on est embarrassé par la difficulté. Un corpus d’œuvres important prend chez les Grecs le nom de Μηχανικά (Mékanika). Le terme machinatio n'est attesté en latin qu'à partir du milieu du I^er siècle, c'est-à-dire à peu près à l'époque où Vitruve doit commencer à rédiger son De architectura. Si l'on poursuit l'enquête terminologique avec les mots de la famille de machina, on s'aperçoit que pour les Romains c'est Archimède qui est généralement associé à la notion de mécanique. Il y a donc bien eu chez les Romains conscience d'une discipline mécanique, mais, hormis chez Vitruve, nous ne trouvons ni définition claire, ni traité qui lui soit exclusivement consacré. Vitruve, dans le troisième chapitre, se contente de faire connaître les machines, il n'essaie pas d'en expliquer les effets[41]. « Lorsque la pesanteur d'un fardeau exige qu'il y ait quatre ou six hommes pour le porter, dit-il, on le met parfaitement en équilibre au milieu des bâtons qui doivent servir, afin que tout le poids de la charge soit divisé de manière que chaque porteur n'ait à soutenir sur son épaule qu'une part proportionnée à leur nombre. Pour cela, le milieu des bâtons où sont attachées les courroies des porteurs, est armé de clous pour empêcher que les fardeaux ne glissent d'un côté ou de l'autre : car s'ils s'écartent du centre, ils pèsent davantage sur l'épaule de celui dont ils se sont approchés. C'est ce qui arrive dit-il dans la statère, balance déjà évoquée, lorsque le poids s'éloigne de l'anse pour avancer vers l'extrémité du fléau[42]. »

La théorie mécanique (ή μηχανική θεωρία) selon Pappus d'Alexandrie (IV^e siècle), « étant utile aux choses multiples et importantes qui se présentent dans la vie, elle mérite à juste titre la plus grande faveur chez les philosophes (προς των φιλοσόφων) et fait l'ambition de tous les mathématiciens (από των μαθημάτων), parce qu'elle est pour ainsi dire la première qui s'applique aux recherches physiques sur la matière constituant les éléments du monde. Cette théorie, organisée au moyen de théorèmes dominés par la matière elle-même, fournit la raison des corps qui se meuvent de par nature et elle en force d'autres en des mouvements de sens opposés, à se déplacer contre nature hors des lieux qui leur sont propres[41] ». Le grammairien Audax classant les arts en trois catégories : ceux qui appartiennent à l'esprit, ceux qui appartiennent au corps et ceux qui appartiennent aux deux, range la mechanica dans cette dernière catégorie. Le mécanicien, praticien ou théoricien est nommé mechanicus[41].

La mécanique entre le XV^e siècle et le XVI^e siècle s’intéresse essentiellement à ce que l'on appelle aujourd'hui la statique, ce que l'on nommait essentiellement la Scientia de ponderibus, traduire la science des poids. Une première approche se raccroche à l'école aristotélicienne, où l'équilibre des corps se règle à la manière d'une balance de tendances opposées au mouvement; la seconde qui lui succède se raccroche à Archimède qui se réduit à l’évaluation du centre de gravité des corps (Barycentre). Entre les deux, Tartaglia (1546-1554), dans ses Questii et inventioni diverse introduit un débat interdisciplinaire important entre physique, architecture, statique et mathématique[43].

Newton introduit la notion de force accélératrice. La force peut être considérée dans deux états différents: À l'état statique, elle exerce une pression ou une traction, mais n'exécute aucun travail. Elle a pour mesure le poids du corps qui lui fait équilibre. À l'état dynamique, elle déplace un corps ou les molécules d'un corps, elle travaille. À l'état statique, une force n'est donc que le poids d'un corps; à l'état dynamique, une force est la force vive ou vis viva du corps en mouvement (ancien nom de l'énergie cinétique et par lequel fut exprimé mathématiquement pour la première fois ce qui sera connu comme la loi de la conservation de l'énergie[44]).