Balistique

Le terme « balistique » a pour étymologie le grec βαλλίστρα (littéralement : ballistra), issu du mot βάλλειν, ballein, « lancer, jeter », au pluriel ballistæ en latin). Avant de devenir un champ d'étude mathématique et physique, la balistique était une discipline empirique. Elle partage son étymologie avec une arme de siège célèbre de l'antiquité, la baliste.

Tout projectile lancé, propulsé ou mis en mouvement dans un référentiel donné va suivre une trajectoire balistique. C'est donc un domaine que l'humanité exploite de manière empirique depuis la nuit des temps pour la chasse et la guerre notamment.

Projectiles de prédilections de la préhistoire, les flèches les plus anciennes ont été découvertes dans la grotte de Fa Hien au Sri Lanka (datées de 48 000 ans)[1], en Tunisie (datées de 50 000 ans)[2], dans la grotte Mandrin en France (datées de 50 000 ans)[3] et dans la grotte de Sibudu en Afrique du Sud (datées de 64 000 ans)[4].

Pointes de flèche du néolithique – Muséum de Toulouse.

On retrouve également à cette époque d'autres moyens de projeter des armes, les propulseurs, qui sont attestés en Europe dès le Paléolithique supérieur, du Solutréen supérieur au début du Magdalénien supérieur, de -23000 à -15000[5] dans une région limitée (Périgord et Pyrénées). Certains éléments de propulseur en matière dure animale (bois de renne ou ivoire de mammouth) étaient richement décorés et constituent des chefs-d'œuvre de l'art mobilier[6] - [7].

Balistique. Walther Hermann Ryff. 1547. La trajectoire dictée par l'impetus, suit la trajectoire postulée par Albert de Saxe et n'a pas encore été influencée par les théories de Tartaglia. Elle est droite à la sortie du canon

Traitant du problème de la dynamique d'un projectile, Jean Buridan (1292-1363) montre que la théorie d'Aristote du mouvement est prise à défaut et remet au goût du jour l'impetus, théorie de Jean Philopon dont il devient le principal promoteur. L'application par Buridan de la théorie de l'impetus au mouvement des projectiles le conduit à une courbe balistique différente de celle donnée par la théorie aristotélicienne. Ce problème a été étudié de manière plus approfondie par un autre savant parisien, Albert de Saxe (1316-1390), qui a distingué trois étapes différentes dans le mouvement des projectiles. Tout d'abord, une étape initiale dans laquelle l'impetus est dominante, et la gravité est considérée comme négligeable, le résultat étant un mouvement en ligne droite. Albert de Saxe définit une étape intermédiaire dans laquelle la gravité se rétablit, et le chemin commence à s'écarter de la ligne droite ; Cette partie du chemin est souvent conçue comme faisant partie d'un cercle. Troisièmement, il postule une étape finale où l'impetus est complètement dépensée, et la gravité seule entraîne le projectile vers le bas le long d'une ligne verticale. La théorie de l'impetus a entraîné une forme améliorée de la courbe balistique, bien que dans un sens purement qualitatif, d'où il aurait été impossible d'en déduire des tableaux de portée de valeur pratique[8].

Le mathématicien italien Niccolò Fontana Tartaglia (1499-1557) fut le premier qui appliqua le raisonnement mathématique au tir de l'artillerie. Encore fortement imprégné de l'impetus, il se donna beaucoup de peine pour démontrer qu'aucune partie de la trajectoire d'un boulet de canon n'est en ligne droite, mais qu'il décrit une courbe dès l'origine de son mouvement hors de la bouche ; il prouva de plus qu'un canon tire le plus loin possible sous l'angle de 45°. Tartaglia passe encore pour avoir découvert le quart de cercle des canonniers. Il était réservé à Galilée et à son élève Evangelista Torricelli de serrer de plus près les lois de la chute des corps. Tartaglia prouva qu'un boulet au sortir du canon se meut suivant une courbe, Galilée démontra que cette courbe était une parabole pourvu que le point de chute du boulet fût dans le même plan que la batterie d'où il avait été tiré et que la pièce fût élevée au-dessus de l'horizon ; il prouva de plus que c'était une moitié de parabole quand le canon dans les mêmes circonstances était pointé horizontalement. Evangelista Torricelli étendit ces découvertes, il montra que le boulet, soit qu'il tombât au-dessus ou au-dessous du plan où se trouvait son point de départ, décrivait une parabole d'une plus ou moins grande amplitude suivant l'angle sous lequel le canon était pointé et suivant la force de la poudre.

La notion d'impetus proclamée en prolongement de la physique d'Aristote disparaîtra au cours du XVII^e siècle pour céder place à celle d'inertie professée par Galilée.

Avant l'époque de Galilée, le tir de l'artillerie était défectueux parce qu'on n'y appliquait pas la science mathématique ; après ce physicien le tir fut défectueux surtout parce que ses théories furent trop exclusivement adoptées et qu'on ne tint pas suffisamment compte des causes d'erreurs accidentelles. « Habitués à nous mouvoir doucement comme nous le faisons à travers l'atmosphère qui se divise devant nous et se referme quand nous avons passé si bien qu'il est devenu le véritable type d'un milieu non résistant, c'est à peine si nous pouvons bien apprécier l'immense résistance qu'il oppose à un projectile animé d'une grande vitesse. » Les expériences de Galilée furent faites sur des corps se mouvant lentement, sur lesquels la résistance de l'air ne pouvait avoir qu'une faible influence, de sorte que leur trajectoire parabolique n'aura été que légèrement déformée, et qu'il n'aura pas apprécié à sa juste valeur l'influence due à cette cause. Cependant Galilée n'ignorait pas que l'air oppose en effet une certaine résistance, mais il crut qu'elle était plus négligeable qu'elle ne l'est réellement. Les idées de Galilée furent adoptées à peu près universellement.

En 1674, Robert Anderson (en) (1668-1696) publie à Londres The Genuine Use and Effects of the Gunne, qui devient très rapidement en Angleterre un ouvrage de référence pour les travaux relatifs à la balistique parabolique, à rapprocher de celui de François Blondel (1618-1686), L'art de jeter les bombes, publié quelques années plus tard en 1683 à Paris. Ces deux textes, qui s'attachent pour l'essentiel à introduire dans la pratique de l'artillerie les principaux résultats de la balistique parabolique établis entre autres par Galilée, Torricelli et Marin Mersenne, ignorent de manière excessives les effets de la résistance de l'air. Bien vite, une querelle oppose, sur la base d'expériences de balistique, Robert Anderson à James Gregory. C'est alors que John Collins (1625-1683), ami de James Gregory, invite John Wallis (1616-1703) et Isaac Newton à donner leurs avis sur la pertinence des thèses en présence, ce qu'il fera une première fois en 1674, puis en 1684 dans son De Motu et en 1687, dans les Philosophiae Naturalis Principia Mathematica[9].

Edmond Halley en 1686 affirme d'une manière positive que pour les gros projectiles métalliques dont le poids surpasse d'un grand nombre de fois celui d'un pareil volume d'air, et dont la force est très grande relativement à la surface sur laquelle l'air est pressé, sa résistance est à peine sensible et il conclut du résultat de l'observation, que si pour un petit projectile léger on peut et on doit tenir compte de la résistance de l'air, dans le tir des grosses et lourdes bombes on peut y faire peu ou point attention[10].

Les artilleurs auraient pu être amenés à douter de la vérité de cette assertion du docteur Halley par l'autorité d'Isaac Newton qui démontre que la courbe décrite par un projectile dans un milieu fortement résistant diffère de la parabole et que la résistance de l'air est assez grande pour produire entre la courbe de projection d'un corps pesant et une parabole une différence sensible et trop considérable pour être négligée. Christian Huygens en 1690 énonce les mêmes principes.

« Malgré le témoignage de deux pareils hommes, et un témoignage encore meilleur celui de la pratique, l'erreur de Galilée continua à se propager. On peut se demander comment il se fit que les erreurs de la théorie parabolique se perpétuèrent lorsqu'il était si facile par la pratique de les démontrer. » La réponse c'est que beaucoup étaient paralysés par le grand nom de Galilée et n'osaient pas se hasarder à penser par eux-mêmes ; il y en avait d'autres qui attribuaient le manque de concordance existant entre la théorie et la pratique à l'intervention de quelque cause ; à toute chose excepté à la vraie. L'incertitude demeura jusqu'en 1742, année où Benjamin Robins publie son traité appelé New Principles of Gunnery qui prend pleinement en considération le frottement de l'air. Les principes développés dans ce traité furent bientôt après confirmés par Leonhard Euler et largement appliqués par la suite[10].

L'utilisation du calcul différentiel et intégral permettra par la suite de mettre en équation de manière complète le mouvement en milieu résistant.

On distingue[11] :

• la balistique intérieure, dont l'objet est l'ensemble des phénomènes se produisant à l'intérieur du canon (mouvement du projectile, détente des gaz...)[12]. Voir chapitre 6.1 de l'article Balistique judiciaire ;
• la balistique extérieure, dont l'objet est le mouvement d'un projectile à l'extérieur du canon. À courte portée, on peut ignorer la courbure du sol et utiliser la formulation décrite plus bas. Cependant la description de la trajectoire d'un missile balistique à longue portée exige une correction tenant compte de la courbure terrestre[13] ;
• la balistique terminale, dont l'objet est l'étude du projectile lorsqu'il frappe la cible (comportement différent selon les types de tirs : tirs à « bout touchant », à « bout portant » — à moins de 50 cm — et à « longue distance »). Voir chapitre 6.3 de l'article Balistique judiciaire.

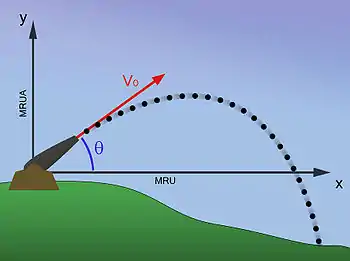
La balistique est l'étude d'un projectile au voisinage du sol[14]. L'objet subit alors trois forces, son poids ${\displaystyle m{\vec {g}}}$, la poussée d'Archimède ${\displaystyle {\vec {F}}}$ et le frottement de l'air ${\displaystyle {\vec {f}}}$.

On fait les hypothèses suivantes :

• le frottement de l'air est négligeable (vitesse faible de l'objet) : ${\displaystyle {\vec {f}}={\vec {0}}}$ ;
• la variation de pression atmosphérique négligeable (variation d'altitude faible) : ${\displaystyle {\vec {F}}={\overrightarrow {cste}}}$.

On obtient un cas particulier du mouvement uniformément accéléré (MUA), car l'accélération ${\displaystyle {\vec {a}}={\vec {g}}+{\vec {F}}/m}$ est constante.

De plus, on fait les hypothèses suivantes :

• la poussée d'Archimède est négligeable (projectile de densité très supérieure à celle de l'air) : ${\displaystyle {\vec {F}}={\vec {0}}}$ ;
• l'altitude et la distance parcourue sont très inférieures au rayon de la planète : ${\displaystyle {\vec {g}}={\overrightarrow {cste}}}$.

Par application du principe fondamental de la dynamique, on obtient une accélération égale à celle de la pesanteur, exprimée par la constante ${\displaystyle g}$ orientée vers le bas : ${\displaystyle {\vec {a}}={\vec {g}}={\overrightarrow {cste}}}$. La trajectoire est alors parabolique : ${\displaystyle {\vec {r}}(t)={\frac {1}{2}}{\vec {a_{0}}}t^{2}+{\vec {v_{0}}}t+{\vec {r_{0}}}}$.

Il est à noter que si l'altitude et la distance parcourue n'étaient pas très inférieures au rayon de la planète, ${\displaystyle {\vec {g}}}$ ne serait plus constant et la trajectoire ne serait plus parabolique, mais elliptique : le projectile aurait alors la trajectoire d'un satellite.

On se place dans un repère orthonormé (Oxyz), orienté de telle sorte que (Oz) soit vertical vers le haut, et (Oy) perpendiculaire à ${\displaystyle {\vec {v_{0}}}}$.

On pose l'accélération du projectile :

${\displaystyle a_{x}=0}$

${\displaystyle a_{y}=0}$

${\displaystyle a_{z}=a_{0}=-g}$

Puis, en intégrant par rapport à ${\displaystyle t}$ :

${\displaystyle v_{x}=v_{0}\cos(\alpha )}$

${\displaystyle v_{y}=0}$

${\displaystyle v_{z}(t)=-gt+v_{0}\sin(\alpha )}$

où ${\displaystyle {\vec {v_{0}}}}$ est la vitesse initiale et ${\displaystyle \alpha }$ est l'angle de ${\displaystyle {\vec {v_{0}}}}$ par rapport à l'horizontale.

Puis, en intégrant par rapport à ${\displaystyle t}$ :

${\displaystyle x(t)=v_{0}\cos(\alpha )\,t+x_{0}}$

${\displaystyle y=0}$

${\displaystyle z(t)=-{\frac {g}{2}}t^{2}+v_{0}\sin(\alpha )\,t+z_{0}}$

où ${\displaystyle x_{0}}$ et ${\displaystyle z_{0}}$ sont les positions initiales de l'objet dans le repère orthonormé (Oxyz).

Par simplification, on choisit le repère (Oxyz) tel que ${\displaystyle x_{0}=0}$ et on obtient :

${\displaystyle t={\frac {x(t)}{v_{0}\cos(\alpha )}}}$

La trajectoire parabolique correspondante dans le plan (Oxz) est alors :

${\displaystyle z(t)=-{\frac {g}{2(v_{0}\cos \alpha )^{2}}}\,x(t)^{2}+\tan(\alpha )\,x(t)+z_{0}}$

La portée atteinte par le projectile à l'horizontale s'obtient par la résolution de l'équation ${\displaystyle z(t)=0}$ :

${\displaystyle p=x(t)_{lorsque\,z(t)\,vaut\,0}={\frac {{v_{0}}^{2}\sin(2\alpha )}{2g}}+{\sqrt {{\frac {({v_{0}}^{2}\sin(2\alpha ))^{2}}{4g^{2}}}+{\frac {2z_{0}(v_{0}\cos(\alpha ))^{2}}{g}}}}}$

Et si ${\displaystyle z_{0}=0}$ :

${\displaystyle p={\frac {{v_{0}}^{2}\sin(2\alpha )}{g}}}$

On voit que, pour une portée ${\displaystyle p}$ cherchée, deux valeurs complémentaires de ${\displaystyle \alpha }$ sont possibles. La plus grande (supérieure à 45°), donne un tir vertical, l'autre un tir plongeant.

L'altitude maximale atteinte par le projectile est ${\displaystyle z_{max}={\frac {{(v_{0}\sin(\alpha ))}^{2}}{2g}}+z_{0}}$.