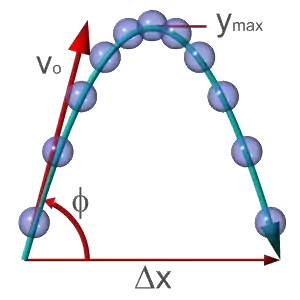
Trajectoire parabolique

En mécanique céleste et en mécanique spatiale, une trajectoire parabolique (ou orbite parabolique[alpha 1]) est une orbite de Kepler dont l'excentricité est égale à 1.

La ligne verte représente une trajectoire parabolique.

L'objet en orbite décrit alors, sur le plan de l'orbite, une parabole dont le foyer est l'objet plus massif.

Le mouvement parabolique s'effectue lorsqu'un projectile est soumis à une vitesse initiale et à la seule accélération de la pesanteur. Un exemple courant de mouvement parabolique est l'obus tiré depuis un canon.

Galilée en 1638 est un des premiers à développer cette théorie (il fallait s'abstraire de la résistance de l'air). Torricelli poursuivra.

Exemples

Lorsqu'on lance un objet en l'air, hormis le cas où il a été lancé rigoureusement à la verticale vers le haut, sa trajectoire est une courbe que l'on peut assimiler à une parabole. Par exemple, le tir d'un boulet de canon ou d'une boule de pétanque décrit une trajectoire quasi-parabolique. Les comètes passent au voisinage du Soleil ou de la Terre sur une orbite « parabolique ». Si un avion effectue une trajectoire parabolique, alors les passagers embarqués se trouvent en impesanteur.

Étude de la trajectoire d'un projectile

Le mouvement d'un objet soumis à un champ de pesanteur uniforme (en l'absence de frottements) est une trajectoire parabolique (balistique).

Soit un corps supposé ponctuel de masse m, étudié dans un repère (O, x, y, z), supposé galiléen z étant la verticale, dirigée vers le haut. Ce corps est placé dans un champ de pesanteur, l'accélération de la pesanteur est g. Le corps est lancé depuis le point (x₀, y₀, z₀) avec une vitesse initiale : ${\vec {V}}_{0}={\begin{pmatrix}V_{x}\\0\\V_{z}\end{pmatrix}}$

On suppose ici qu'il n'y a pas de composante de vitesse suivant l'axe ${\vec {y}}$ , tout le mouvement a donc lieu dans un plan parallèle au plan (xOz). On note t le temps.

Résolution de l'équation

La seule force à laquelle soit soumis le corps est la gravité (on peut affiner le problème en ajoutant par exemple le frottement dû à l'air). La seule accélération imprimée au corps est donc l'accélération de la pesanteur.

${\vec {a}}={\begin{pmatrix}0\\0\\-g\end{pmatrix}}$

Pour en déduire la vitesse, il suffit d'intégrer l'accélération :

${\vec {V}}={\begin{pmatrix}C1\\C2\\-g\,t+C3\end{pmatrix}}$

C1, C2 et C3 sont des constantes d'intégration, données par les conditions initiales. En effet à t = 0, ${\vec {V}}={\vec {V}}_{0}$ , soit ${\begin{pmatrix}C1\\C2\\-g\times 0+C3\end{pmatrix}}={\begin{pmatrix}V_{x}\\0\\V_{z}\end{pmatrix}}$ ,

d'où C1 = V_x, C2 = 0 et C3=V_z.

On a donc :

${\vec {V}}(t)={\begin{pmatrix}V_{x}\\0\\-g\,t+V_{z}\end{pmatrix}}$

Pour obtenir l'équation de la trajectoire, il faut intégrer la vitesse :

${\overrightarrow {OM}}(t)={\begin{pmatrix}V_{x}\,t+C4\\C5\\-{1 \over 2}\,g\,t^{2}+V_{z}\,t+C6\end{pmatrix}}$

C4, C5 et C6 sont (à nouveau) des constantes d'intégration qui seront déterminées à l'aide des conditions initiales.

A t = 0, ${\overrightarrow {OM}}(0)={\overrightarrow {OM_{0}}}$

Donc ${\begin{pmatrix}V_{x}\times 0+C4\\C5\\-{1 \over 2}\,g\times 0^{2}+V_{z}\times 0+C6\end{pmatrix}}={\begin{pmatrix}x_{0}\\y_{0}\\z_{0}\end{pmatrix}}.$
d'où ${\overrightarrow {OM}}(t)={\begin{pmatrix}V_{x}\,t+x_{0}\\y_{0}\\-{1 \over 2}\,g\,t^{2}+V_{z}\,t+z_{0}\end{pmatrix}}$

Équation de la trajectoire

On peut donner l'équation sous la forme z = f(x) en remplaçant t dans l'équation de z par l'expression qu'on en tire dans l'équation de x, soit ${x-x_{0} \over V_{x}}$

On obtient donc : $z(x)=-{1 \over 2}\,g\,\left({x-x_{0} \over V_{x}}\right)^{2}+V_{z}\,{x-x_{0} \over V_{x}}+z_{0}$

$z(x)=-{1 \over 2}\,{g \over V_{x}^{2}}\,x^{2}+\left({V_{z} \over V_{x}}+{g \over V_{x}^{2}}x_{0}\right)\,x-{1 \over 2}\,{g \over V_{x}^{2}}\,x_{0}^{2}-{V_{z} \over V_{x}}\,x_{0}+z_{0}$

L'équation de ce mouvement indique bien la parabole qui donne son nom à ce mouvement. Cette équation permet aussi de retirer plusieurs informations utiles comme les endroits où le projectile touche le sol (résoudre l'équation z(x) = 0).

L'équation se simplifie donc notablement si on choisit l'origine des axes au point de lancer :

$z(x)=-{1 \over 2}\,{g \over V_{x}^{2}}\,x^{2}+{\frac {V_{z}}{V_{x}}}\,x$

Souvent la notation des artilleurs est utilisée : on appelle angle $\phi$ de hausse du canon, l'angle que fait la trajectoire au départ avec l'horizontale. La vitesse au départ étant notée $V_{0}$ , alors $V_{x}=V_{0}.\cos(\phi )$ et $V_{z}=V_{0}.\sin(\phi )$ . L'équation s'écrit alors :

$z(x)=-{\frac {1}{2}}{\frac {g}{V_{o}^{2}}}x^{2}[1+\tan ^{2}(\phi )]+x.\tan(\phi )$

Si l'artilleur désire atteindre une cible située en M(xo, zo), il devra régler la hausse du canon, c'est-à-dire choisir $\tan(\phi )$ ; comme il apparaît sur cette équation du second degré en $\tan(\phi )$ , il y aura deux solutions, une solution double ou pas de solution (voir parabole de sûreté).

Approche mathématique

Une autre approche, plus directe, peut être faite, en trouvant directement le polynôme du second degré donnant la hauteur du projectile en fonction de sa distance au sol du point de lancement.

Dans le même repère que précédemment, le projectile est lancé depuis un point $P(x_{P};y_{P})$ à une vitesse initiale $v_{0}$ , formant un angle $\alpha$ avec l'axe horizontal.

Sans tenir compte de la gravité $g$ , la hauteur en fonction de la distance au sol est donc $y=y_{P}+v_{0}t\sin(\alpha )$ , où $t$ désigne le temps écoulé depuis le lancement du projectile. Cette première expression est en fait la simple projection trigonométrique de la droite de distance parcourue sur l'axe des ordonnées, représentant la hauteur. C'est donc l'équation de la droite $D_{1}$ formant un angle $\alpha$ avec l'axe des abscisses, et le terme $v_{0}t$ correspond à la distance $d$ parcourue sur cette droite. En ajoutant l'effet de la gravité, à savoir la différence de hauteur provoquée par la chute du projectile, on obtient :

$h(t)=y_{P}+v_{0}t\sin(\alpha )-{\frac {1}{2}}gt^{2}$ qui est l'équation donnant la hauteur en fonction du temps. À ce stade, il suffit alors d'éliminer $t$ et d'introduire $x$ , la distance. Pour cela, on utilise cette relation dans le plan :

$v_{0}t\cos(\alpha )=x$ et par conséquent, $t={\frac {x}{v_{0}\cos(\alpha )}}$ . On remplace cette expression de $t$ dans l'équation :

$h(x)=y_{P}+v_{0}\left({\frac {x}{v_{0}\cos(\alpha )}}\right)\sin(\alpha )-{\frac {1}{2}}g\left({\frac {x}{v_{0}\cos(\alpha )}}\right)^{2}$ , puis par simplification, on obtient :

$h(x)=y_{p}+x\tan(\alpha )-{\frac {g}{2v_{0}^{2}\cos ^{2}(\alpha )}}x^{2}$ qui est la forme développée du polynôme du second degré, où $a=-{\frac {g}{2v_{0}^{2}\cos ^{2}(\alpha )}}$ , $b=\tan(\alpha )$ et $c=y_{P}$ . Ainsi, pour trouver par exemple quelle sera la hauteur maximale atteinte et en quelle valeur de $x$ , il n'y a qu'à étudier la fonction du second degré avec les paramètres afin de trouver $\alpha$ et $\beta$ . De même, pour savoir la distance à laquelle le projectile retombera au sol, il suffit de résoudre $h(x)=0$ . La solution sera la seule valeur de $x$ cohérente pour tout $x_{P}=0,y_{P}=0$ (on se place à l'origine du repère pour lancer le projectile afin d'éviter les cas de non-solutions dans $\mathbb {R}$ .

Graphique

Exemple d'un tir parabolique.

Ici $\phi$ est l'angle que fait le vecteur vitesse initiale avec l'horizontale :
$\phi =\arctan \left({\frac {V_{y}}{V_{x}}}\right)$

Notes et références

Le terme d'orbite parabolique est malencontreux, car une orbite est définie comme une courbe fermée, ce qui n'est pas le cas de la parabole.

Voir aussi

Articles connexes

Balistique
Chute libre (physique)
g, accélération de la pesanteur
Apesanteur
Parabole de sûreté
Portée
Vol parabolique d'un Airbus A300 ZERO-G, celui-ci effectuant 15 paraboles successives en « ressource » à surpesanteur constante de 1,8 g, puis en apesanteur à 0 g, tout en conservant une vitesse horizontale constante, décrivant donc une parabole à l'analogue de la courbe de la trajectoire en fonction du temps
Accélération
Montagnes russes, en particulier les bosses en « Top Hat » (sommet en chapeau), profilés paraboliquement pour des sensations d'hyperpesanteur et apesanteur

Liens externes

Cet article est issu de wikipedia. Text licence: CC BY-SA 4.0, Des conditions supplémentaires peuvent s’appliquer aux fichiers multimédias.