Balance hydrostatique

La balance hydrostatique se présente comme une balance ordinaire à fléau munie de deux plateaux. Sous chaque plateau est en outre placé un crochet qui permet d'y suspendre des objets.

Mise en évidence du principe d'Archimède

Mise en évidence de la poussée d'Archimède avec une balance hydrostatique

On suspend, sous le premier plateau, un objet et on équilibre le fléau en déposant des poids dans le second plateau. On plonge alors l'objet dans un récipient rempli d'eau tout en le laissant accroché au premier plateau. Le premier plateau remonte alors. Le poids apparent de l'objet est donc moindre dans l'eau que dans l'air.

On recommence alors l'expérience, en ajoutant sur le premier plateau un récipient vide, en équilibrant les deux plateaux et en plongeant l'objet dans un récipient rempli d'eau à ras bord. L'objet plongé dans l'eau chasse une quantité d'eau qui est précieusement récupérée. Le premier plateau remonte alors. On verse ensuite dans le récipient situé sur le premier plateau l'eau récupérée : la balance revient à l'équilibre.

En joaillerie et en gemmologie, on utilise des balances hydrostatiques pour évaluer la densité d'une gemme. La balance hydrostatique permet de déterminer le poids de la pierre dans l'air, puis son poids dans l'eau. En divisant son poids dans l'air par la différence des deux poids on obtient sa densité.

Ainsi, si une pierre pèse 2,4 grammes dans l'air et 1,8 gramme dans l'eau, sa densité est de

${\displaystyle {\frac {2,4}{2,4-1,8}}=4}$

En pratique les balances hydrostatiques modernes font directement la soustraction[2].

En 1586, Galilée imagine et réalise une balance permettant de déterminer la densité des objets mais aussi la composition d'un alliage[3]. Sa recherche s'inspire de la légende d'Archimède et de la couronne de Hiéron. Galilée utilise une balance romaine dans laquelle l'équilibre des fléaux est réalisé en déplaçant une masselotte sur le bras ne supportant pas l'objet.

L'expérience consiste à accrocher l'objet au premier bras et à déplacer la masselotte jusqu'à arriver à l'équilibre. Il mesure alors la distance OA séparant la masselotte de l'axe de la balance. Il plonge alors l'objet dans l'eau. Le poids apparent de l'objet étant moindre, il lui faut déplacer la masselotte vers l'axe de la balance en un point B pour équilibrer le fléau.

Galilée démontre alors que la densité de l'objet se détermine comme le rapport de longueurs : ${\displaystyle {\frac {OA}{AB}}}$.

La petite balance de Galilée avec les marqueurs des 4 positions de la masselotte, dans l'air (A), dans l'eau avec le métal 1 (B1), dans l'eau avec le métal 2 (B2), dans l'eau avec l'alliage (Ba)

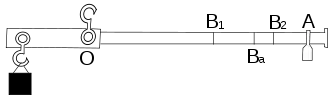
Il présente ensuite une méthode pour déterminer la composition d'un alliage de deux métaux. Il lui faut pour cela trois objets de même masse, l'un composé du métal 1, le second du métal 2 et le troisième étant un alliage de ces deux métaux. Puisque les trois objets ont même masse, en les accrochant au bras de la balance, il faut placer la masselotte au même point A pour équilibrer le fléau. Il trempe alors successivement les trois objets dans l'eau et note successivement les trois nouvelles positions de la masselotte ${\displaystyle B_{1}}$ pour le métal 1, ${\displaystyle B_{2}}$ pour le métal 2 et ${\displaystyle B_{a}}$ pour l'alliage.

Il énonce alors que la position de ${\displaystyle B_{a}}$ est le barycentre des points ${\displaystyle B_{1}}$ et ${\displaystyle B_{2}}$ affectés des masses ${\displaystyle m_{1}}$ et ${\displaystyle m_{2}}$ des deux métaux dans l'alliage. Il suffit donc de mesurer les distances ${\displaystyle B_{2}B_{a}}$ et ${\displaystyle B_{1}B_{a}}$ pour connaitre la composition de l'alliage: la part de métal 1 est de ${\displaystyle {\frac {B_{2}B_{a}}{B_{1}B_{2}}}}$ et celui du métal 2 est de ${\displaystyle {\frac {B_{1}B_{a}}{B_{1}B_{2}}}.}$

Il décrit ensuite comment réaliser une telle balance et comment mesurer avec précision ces différentes longueurs à l'aide de spires.

• Charles Drion, Emile Fernet, Traité de physique élémentaire, V. Masson, 1869;
• Émile Namer, Le traité de « La balance hydrostatique » de Galilée. In: Revue d'histoire des sciences et de leurs applications. 1964, Tome 17 n°4. pp. 397-403.

• Pesée hydrostatique
• Hydromètre
• Pycnomètre