Histoire des probabilités
L'histoire des probabilités a commencé avec celle des jeux de hasard. Bien que quelques calculs de probabilité soient apparus dans des applications précises au Moyen Âge, ce n'est qu'au XVIIe siècle que la théorie des probabilités est élaborée. Elle évolue sans vrai formalisme pendant deux siècles autour du célèbre problème des partis, de problèmes d'urnes ou d'autres problèmes issus de jeux. Apparaît alors au XXe siècle la théorie classique des probabilités basée sur la théorie de la mesure et la théorie de l'intégration. Cette théorie s'est depuis lors diversifiée dans de nombreuses applications.
Les discussions entre scientifiques, la publication des ouvrages et leur transmission étant difficiles à certaines époques, certaines questions historiques restent difficiles à résoudre ; c'est le cas de la paternité de la théorie des probabilités.
Les premières utilisations et idées

La théorie des probabilités est une mathématisation de l'incertitude et du caractère imprévisible des phénomènes. L'incertitude de la situation présente et à venir a d'abord été attribuée au destin, à la nature ou à des divinités[1].
Pendant l'antiquité, le hasard n'a pas été un objet d'étude à proprement parler. Cependant le hasard a été utilisé pour le divertissement dans les jeux de hasard comme les jeux de dés en terre cuite[2] présents dans l'Égypte antique (du XXXIIe siècle av. J.-C. au Ier siècle av. J.-C.), en Mésopotamie (IIIe millénaire av. J.-C.) ou encore en Inde à la même époque[3]. La notion d'équité était déjà présente puisque certains dés avaient été pipés volontairement[2]. Les cartes étaient également très présentes, elles sont d'abord apparues en Chine, Inde, Arabie et Égypte pour n'arriver que beaucoup plus tard à Venise (1377), Nuremberg (1380) et à Paris (1397)[3]. Le hasard était également utilisé comme moyen de prise de décision[4], par exemple pour décider dans quel ordre les équipes vont se rencontrer lors d'un sport.
Les philosophes de la Grèce antique ont abordé la question de la définition de ce concept d'incertitude. Le concept de probabilités chez Aristote (IVe siècle av. J.-C.) est défini dans les Topiques :
« Sont probables les opinions qui sont reçues par tous les hommes, ou par la plupart d’entre eux, ou par les sages, et parmi ces derniers, soit par tous, soit par la plupart, soit enfin par les plus notables et les plus illustres »
Ce qui rend une opinion probable chez Aristote est son caractère généralement admis[a 1]. Il distingue les évènements nécessaires qui doivent nécessairement se produire ou très fréquemment, des évènements fortuits, accidentels ou contingents qui peuvent se produire ou non[1].
Cette idée d'Aristote a été initiatrice pour mieux définir la notion de probabilité chez de nombreux auteurs . Dans la traduction de Cicéron des Topiques d'Aristote (Ier siècle), probable est traduit par probabilis ou par verisimilis, la notion de vraisemblance est alors associée à celle de probabilité ce qui aura un impact au cours du Moyen Âge puis de la Renaissance avec les commentaires successifs de l'œuvre d'Aristote[a 2]. Au XIIIe siècle, dans une traduction de l'éthique à Nicomaque d'Aristote par Oresme, le terme probabilité désigne « le caractère de ce qui est probable »[a 3].
Certaines ébauches de calculs apparaissent dans des applications précises. Durant la Rome antique, le hasard est évalué pour décider de la valeur des rentes viagères, c'est-à-dire faire un pari sur la durée de vie[2]. Ces calculs sont basés sur des tables de valeurs, certaines du jurisconsulte Ulpien (IIIe siècle) ont été retrouvées. Bien que le concept de probabilité au sens « statistique » ne soit pas encore élaboré, des premiers « raisonnements probabilistes » apparaissent[a 4].
Notion moderne de probabilité
L'apparition de la notion de « risque », préalable à l'étude des probabilités, n'est apparue qu'au XIIe siècle pour l'évaluation de contrats commerciaux avec le Traité des contrats de Pierre de Jean Olivi[a 5]. Cette idée s'est développée pendant le Moyen Âge, au XIIIe siècle et XIVe siècle ; des bourses ont été créées pour assurer les transports maritimes dépendant des fluctuations météorologiques[2] et au XVIe siècle avec la généralisation des contrats d'assurance maritime[a 4].
Une des premières références connues de calculs de probabilités est un calcul élémentaire sur le poème La Divine Comédie qui n'apparaît qu'au XVe siècle pendant la Renaissance[4].
Apparaissent alors quelques références aux probabilités dans un traité posthume de Girolamo Cardano (Jérôme Cardan en français) publié[4] en 1663 titré : Liber de Ludo ALeæ[3]. Il étudie les différentes combinaisons possibles obtenues à partir de un, deux ou trois dés, truqués ou non et il expose le principe d'équiprobabilité ou équipossibilité[5] :
« Aussi il y a une règle générale, que nous devons considérer le circuit entier [i.e. toutes les possibilités], et le nombre de ces lancers qui représente en combien de façons les résultats favorables peuvent se produire, et comparer ce nombre au reste du circuit, et les paris mutuels devront être posés selon cette proportion, de sorte qu'on puisse disputer en termes égaux. »
Cette approche utilise l'intuition d'un comportement à long terme, c'est-à-dire correspondant à un sentiment empirique de la loi des grands nombres, elle est qualifiée de fréquentiste. La notion d'indépendance était connue par Cardan puisqu'il utilise la multiplication des probabilités[6].
Les idées se propagent en Italie et en France, en effet Galilée écrit entre 1620 en 1718 son petit mémoire sur le jeu de dés intitulé Sopra le Scoperte de i Dadi[3] dans lequel il suppose l'équipossibilité des lancers. Cette notion d'équipossibilité se retrouve également, plus tard, dans la correspondance de Pierre de Fermat et dans celle de Pierre-Simon de Laplace.
Étymologie au Moyen Âge et probabilisme
Le terme probabilité a été utilisé au Moyen Âge en jurisprudence. Il est issu du latin « probare » qui signifie « prouver » ainsi désigne l'appréciation des éléments de preuves lors d'un jugement tels que les preuves, les indices ou les témoignages. En 1361, le calcul des probabilités est alors une « science dont le but est de déterminer la vraisemblance d'un évènement »[7]. Une opinion est alors probable si elle « a une apparence de vérité ». Le mathématicien Marin Mersenne utilise ces termes en 1637[7] :
« Question XXIV : Peut-on savoir au vray à quelle heure, à quel jour, en quel mois, et en quelle année le monde a commencé, et quand il finira.
Il est certain que nul ne peut sçavoir sans révélation en quelle année ... Dieu a creé le monde, car les plus sçavans Chronologues avoüent ingenuëment qu'ils ne vont qu'à tastons, et qu'ils n'ont que des conjectures, ou des probabilitez,… »
Les avis et opinions des autorités morales et religieuses étaient probables. Sous l'influence entre autres de Bartolomé de Medina et des jésuites, il apparut alors au XVIe siècle et XVIIe siècle une doctrine religieuse appelée probabilisme qui « juge impossible d'arriver à la certitude et recommande de s'en tenir à ce qui est le plus probable »[7].
Cette théologie morale a été très critiquée à partir du milieu du XVIIe siècle[a 6] comme introduisant le relativisme moral, en particulier par les jansénistes et par Blaise Pascal, qui sera, par ailleurs, l'un des fondateurs du traitement mathématique du probable[a 7].
Début de la théorie des probabilités
Paternité
Le véritable début de la théorie des probabilités date de la correspondance entre Pierre de Fermat et Blaise Pascal en 1654 au sujet d'une désormais célèbre question posée par Antoine Gombaud (dit chevalier de Méré) : le problème des partis[8] ou problèmes des points[9]. « Il avait pour objet de déterminer la proportion suivant laquelle l'enjeu doit être partagé entre les joueurs lorsqu'ils conviennent de ne point achever la partie, et qu'il leur reste à prendre pour la gagner, des nombres de points inégaux. Pascal en donna le premier la solution, mais pour le cas de deux joueurs seulement ; il fut ensuite résolu pour Fermat, dans le cas général d'un nombre quelconque de joueurs. » (Poisson[8]). Citons les travaux : Adresse à Académie parisienne de mathématiques de Pascal (1654)[10].
À la suite d'un séjour à Paris[11] en 1655, Christian Huygens prend connaissance de cette discussion à l'Académie Parisienne et publie en 1657 le premier traité sur la théorie probabiliste : De ratiociniis in ludo aleae (raisonnements sur les jeux de dés). C'est dans une lettre adressée à Frans Van Shooten, qui a traduit son traité en latin dans Mathematische Oeffeningen, qu'il attribue la paternité de la théorie des probabilités à Pascal et Fermat[11] :
« Il faut savoir d'ailleurs qu'il y a un certain temps que quelques-uns des plus Célèbres Mathématiciens de toute la France se sont occupés de ce genre de calcul, afin que personne ne m'attribue l'honneur de la première Invention qui ne m'appartient pas. »
Puisqu'il fallait un certain délai entre l'écriture[11], la publication des œuvres et la diffusion de ces dernières, la paternité de la théorie des probabilités n'est pas unanime. Si la date de publication compte, c'est à Huygens que revient l'honneur d'être appelé le père de la théorie des probabilités, cependant si la date d'écrit compte, c'est à Jérôme Cardan que revient ce « titre »[8]. Cependant la mauvaise réputation de Cardan a fait pencher la paternité sur Pascal et Fermat[8]. Leibniz (1646-1716) ne cite que Pascal, Fermat et Huygens ; Montmort (1678-1719) cite Cardan mais d'une manière restrictive ; Montucla (1725-1799), Laplace (1749-1827) et Poisson (1781-1840) ne citent que Pascal et Fermat[8].
 Cardan
Cardan Pascal
Pascal Poisson
Poisson Huygens
Huygens
Les premières évolutions au XVIIIe siècle
Le traité de Huygens est resté le seul ouvrage important de la théorie des probabilités jusqu'au début du XVIIIe siècle, il fut traduit en 1692 en anglais par un auteur anonyme, aujourd'hui attribué à John Arbuthnot. Peut-être du fait que cette théorie ne semblait pas avoir d'applications en sciences[12].
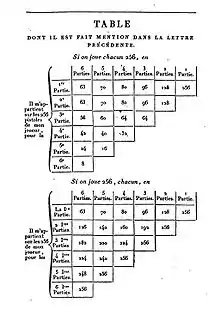
Plusieurs ouvrages sur les probabilités suivent le premier traité de Huygens. Pierre Rémond de Montmort publie en 1708 l'un des premiers : l'Essai sur les Jeux de Hasard contenant le binôme de Newton, des problèmes de jeux de cartes et le problème des partis. de Fontenelle en fit des éloges[13]. Les problèmes se posent ainsi, à propos de la durée d'un jeu de cartes :
« Sur la durée des parties que l'on joue en rabattant… On demande combien il y a à parier que la partie qui peut durer à l'infini sera finie en un certain nombre déterminé de coups au plus. »
— Essay, de Montmort, 1713[14]
On reconnaît ici la probabilité (« à parier ») qu'une variable (« la durée de la partie ») soit plus petite qu'une valeur (« certain nombre déterminé »), il s'agit de la fonction de répartition de la loi de probabilité de la durée d'une partie. Cependant le terme « probabilité » n'apparait toujours pas dans les écrits, il avait une signification autre (voir Étymologie au Moyen Âge et probabilisme). Les problèmes se posent en fonction des « chances » ou des « hasards » des joueurs[12].

Abraham de Moivre publie en 1718 The Doctrine of Chances (en anglais) contenant des problèmes combinatoires dont la formule de Stirling, des probabilités conditionnelles ainsi qu'une approximation de loi normale par une loi binomiale, c'est la première version du théorème central limite dit théorème de Moivre-Laplace[9]. Les énoncés mathématiques sont plus précis mais n'utilisent pas le formalisme actuel[15] :
« Corollaire 8.
La rapport que, dans une puissance infinie d'une binomiale, dénotée par n, le plus grand terme porte à la somme de tout le reste, sera justement exprimé par la fraction , où c désigne, comme auparavant, la circonférence d'un cercle dont le rayon égale l'unité. »
Par ce type d'énoncés, de Moivre en arrive à la courbe appelée normale, mais il ne la considère que comme approximation et non comme densité d'une loi normale[16]. Ce traité reste le traité majeur en théorie des probabilités jusqu'à la parution du grand traité de Laplace en 1812 : Théorie analytique des probabilités[15].
La famille Bernoulli

L’œuvre posthume de Jacques Bernoulli : Ars Conjectandi est publiée en 1713. Elle reprend les calculs de Huygens de divers problèmes combinatoires notamment sur le binôme de Newton[9]. Son traité contient également une description de l'estimation d'un phénomène aléatoire sous forme de fréquences :
« Ce qu'il n'est pas donné d'obtenir a priori l'est du moins a posteriori, c'est-à-dire qu'il sera possible de l'extraire en observant l'issue de nombreux exemples semblables. »
C'est la relation entre la probabilité d'un évènement et l'observation de celui-ci, Bernoulli appelle ce résultat son « théorème d'or ». Le nom de « loi des grands nombres » pour ce type de résultats a été donné plus tard probablement au XIXe siècle par Poisson. Ce résultat est cependant une version généralisée du théorème actuel appelé « loi des grands nombres »[17].
Nicolas Bernoulli publie en 1711 sa thèse de doctorat où apparait pour la première fois la loi uniforme discrète[9]. Daniel Bernoulli étudie, autour de 1732, des applications du calcul des probabilités aux problèmes d'assurance, à l'astronomie, au calcul d'erreur ou au paradoxe de Saint-Pétersbourg[9]. Dans les mêmes années, Leonhard Euler contribue également à des questions d'assurance[9]. Jean le Rond D'Alembert étudie de même le paradoxe de Saint-Pétersbourg et énonce la règle actuelle du calcul de l'espérance d'une variable aléatoire discrète[9].
Bayes et ses applications
Thomas Bayes énonce, à titre posthume en 1764 dans un article intitulé An essay towards solving a problem in the doctrine of chances[18], une première version d'une formule dite théorème de Bayes utilisant des probabilités conditionnelles[9]. Ce théorème est également appelé problème inverse ou probabilité inverse[19] et a été étudié par de nombreux auteurs cependant le premier à donner une formulation précise de ce problème de probabilité inverse est Pierre-Simon de Laplace en 1774 dans son mémoire Sur la probabilité des causes[18] :
« On suppose qu'un évènement de probabilité positive peut être obtenu par n'importe laquelle des causes mutuellement exclusives et exhaustives, toutes de probabilité positive. Ainsi, pour chaque i :
- . »
Le naturaliste Georges-Louis Leclerc de Buffon publie en 1777 son Essai d'Arithmétique Morale dans lequel apparait des liens entre les probabilités et la géométrie, et en particulier, le problème de l'aiguille de Buffon[9].
Les travaux du XIXe siècle
Joseph-Louis Lagrange publie vers 1770 un mémoire contenant des problèmes de durée d'un jeu de hasard et utilisant des lois continues[9]. Débute alors la considération du caractère continu des probabilités.
Au début du XIXe siècle, plus précisément en 1812, Laplace publie son traité intitulé Théorie analytique des probabilités dans lequel il présente des résultats asymptotiques étant ainsi un des premiers ouvrages à distinguer des énoncés de principes probabilistes aux estimations des probabilités observées à la suite d'une expérience[20]. Cependant la distinction aujourd'hui usuelle entre le signe somme et le signe intégrale n'était pas observée à l'époque de Laplace[21]. Il énoncent alors ces résultats à propos de problèmes d'urnes en utilisant des rationnels[21] :
« Le rapport du nombre de billets blancs au nombre total des billets contenus dans l'urne peut être un quelconque des nombres fractionnaires compris depuis 0 jusqu'à 1. »
En augmentant le nombre de « billets » à l'infini, Laplace énonce alors une première version rigoureuse du théorème central limite[22] :
« on voit donc qu'en négligeant les quantités infiniment petites, nous pouvons regarder comme certain que le rapport du nombre de billets blancs au nombre total de billets est compris est compris entre les limites et , étant égale à , étant plus grand que 2 et moindre que 3; partant peut être supposé moindre qu'aucune grandeur posée. »
Ici le théorème central limite est vu par l'intermédiaire d'intervalles de confiance, c'est-à-dire en donnant l'imprécision de la convergence d'une somme vers la moyenne obtenue pour la loi des grands nombres[a 8]. Les travaux de Laplace resteront des travaux de référence jusqu'à la fin du XIXe siècle et au début du XXe siècle[23].
Début d'un enseignement
À la fin du XVIIIe siècle, autour de 1792, le politicien et mathématicien Nicolas de Condorcet ambitionne le développement d'un enseignement des probabilités pour « donner la vérité aux hommes et leur donner accès au bonheur »[24]. En 1816, Sylvestre-François Lacroix édite le premier ouvrage d'enseignement des probabilités intitulé traité élémentaire de calcul des probabilités[25].
Dans ces mêmes années, Condorcet publie l'Élemens du calcul des probabilités et son application aux jeux de hasard, à la loterie, et aux jugemens des hommes dans lequel il aborde la notion d'équiprobabilité dans des exemples combinatoires basés sur les jeux de hasard. Sans être un livre scolaire, le but de cet ouvrage était d'expliquer les mathématiques avec la même facilité que lorsqu'il s'agit de lire un roman[26].
Lorsque l'école polytechnique est créée en 1794, l'enseignement débute avec le cours du calcul des probabilités de Joseph Fourier. Citons également François Arago qui enseigna des calculs de probabilité dans son cours d'arithmétique sociale[27].
Les critiques
La théorie des probabilités a toujours pris une place à part dans le domaine des mathématiques. La Faculté des sciences de Paris, créée en 1808, ne contenait pas de chaire de calcul des probabilités. La première chaire n'est créée qu'en 1834[28].
La théorie des probabilités a d'abord été considérée comme une partie des mathématiques appliquées. Le philosophe Auguste Comte la désigne comme « prétendue théorie des probabilités »[29], le courant philosophique du positivisme (1830-1845) fait une critique radicale : « prétendre évaluer une probabilité est une escroquerie scientifique et une malhonnêteté morale »[25].
Associer une science à l'incertitude du hasard, a soulevé plusieurs questionnements chez les mathématiciens : Joseph Bertrand en 1900 écrit : « Comment oser parler des lois du hasard ? Le hasard n'est-il pas l'antithèse de toute loi ? »[10].
Théorie classique des probabilités
Fondements
La théorie des probabilités va prendre un nouvel essor vers le début du XXe siècle grâce à l’introduction de nouveaux concepts comme les mesures et l’intégration.
Axel Harnack introduit en 1881 la notion d’ensemble discret, puis en 1882 le concept d’« égalité en général » qui est précurseur de l’égalité presque sûre[30]. Les mesures apparaissent sous différentes définitions suivant les travaux de Georg Cantor (1884), Giuseppe Peano (1887) ou Camille Jordan (1892)[30]. Mais c’est à Émile Borel que l’on attribue la paternité de la théorie de la mesure avec l’introduction d'ensembles de mesure nulle en 1897, et de la classe des sous-ensembles ouverts de qu’il mesure à partir de la longueur des intervalles. Cette classe portera plus tard le nom de « borélienne »[30]. La théorie des probabilités est simplement une branche de la théorie de la mesure avec ses propres applications, comme le souligne plus tard Joseph Leo Doob en 1953[31].
En 1901, Henri-Léon Lebesgue utilise cette théorie de la mesure pour développer la théorie de l'intégration qui généralise l’intégrale de Riemann[30]. Sous l’impulsion de Johann Radon en 1913, cette théorie se généralise sur puis sur un ensemble plus abstrait muni d'une tribu[30]. La fin de cette généralisation est estimée à 1930 avec la décomposition de Radon-Nikodym-Lebesgue et l’existence des densités[30].
C’est à partir de 1930 que Andreï Kolmogorov fonde mathématiquement la théorie des probabilités[29]. Il publie en 1933 son travail fondamental : Grundbegriffe des Warscheinlichkeitrechnung en posant les trois axiomes des probabilités qui définissent de manière rigoureuse et consistante les probabilités[31]. Le mathématicien Jean Dieudonné souligne plus tard en 1977 que[31] :
« Le calcul des probabilités, en tant que discipline, n’existe guère que depuis 1933, comme partie de la théorie moderne de l’Intégration ; elle a hérité de ses propres problèmes et même de son langage, des trois siècles antérieurs au cours desquels le Calcul des probabilités était un mélange de raisonnements d’allure mathématique et de considérations plus ou moins intuitives sur le rôle et l’évaluation du hasard dans les comportements humains ou les phénomènes naturels. »
L'axiomatique de Kolmogorov n'a cependant pas fait directement le consensus auprès de la communauté mathématique et n'a été largement reconnue qu'en 1959[32]. Par exemple, Gustave Choquet souligne en 1962 que le groupe Bourbaki ferme à ses disciples les portes du calcul des probabilités[33]. Dans les années 1960, Mark Kac considère que la théorie des probabilités est plus proche de l'analyse, de la physique et de la statistique que de la théorie de la mesure[34].
 Borel
Borel Lebesgue
Lebesgue Kolmogorov
Kolmogorov
Notons que la théorie des probabilités est proche de la statistique, notamment dans les domaines d'utilisations de données statistiques. Ces deux sciences sont toutefois séparées comme l'expliquent les travaux en 1930 de Karl Pearson, Egon Sharpe Pearson, Jerzy Neyman, Ronald Aylmer Fisher et William Gosset[35].
Évolution au XXe siècle
- Théorème central limite
Redonnons les grandes étapes de la découverte de ce théorème central limite. Abraham de Moivre énonce une première version de ce résultat[36] dans son œuvre de 1718 (et traduit en anglais en 1738) dans le cas où (cas des variables aléatoires indépendantes de loi de Bernoulli de paramètre ). Il est à noter que De Moivre n'écrit pas son résultat sous forme de limite mais sous forme d'approximation. Alors qu'en 1810, Pierre-Simon de Laplace généralise et explicite cette approximation[37], il publie en 1812 le théorème de convergence pour variables aléatoires de moyenne et de variance fixée[38]. Pafnouti Tchebychev a été le premier[39] à formuler en 1887 le théorème sous la forme de convergence des fonctions de répartition, la première preuve du théorème moderne est donnée[a 8] par Paul Lévy en 1910, puis Richard von Mises énonça[40] le résultat sous forme intégral en 1919. Le nom théorème central limite (central limit theorem en anglais) vient des travaux de George Pólya de 1920 dans lesquels il écrit que le densité de probabilité gaussienne peut être obtenue par un théorème limite qui joue un rôle central en théorie des probabilités[41]. L'abréviation TCL (CLT en anglais) est alors utilisée.
- Processus stochastiques

L'origine des processus stochastiques date du début du XXe siècle et ont été introduits pour modéliser des phénomènes temporels où intervient le hasard, en mécanique statistique par exemple. les premiers physiciens à les utiliser sont Willard Gibbs, Ludwig Boltzmann, Henri Poincaré, Marian Smoluchowski ou Paul Langevin[42]. Les bases théoriques sont apparus plus tard dans les années 1930-1940 grâce aux travaux des mathématiciens Joseph Leo Doob et Andreï Kolmogorov, entre autres[42]. Apparait alors le terme stochastique issu du grec « stokastikos » signifiant « conjectural »[42]. En 1902[a 9], Andreï Markov posa les bases de la théorie des processus à temps fini possédant la propriété de Markov : le futur du processus ne dépend que du présent et non du passé. Ces processus seront appelés processus de Markov. Louis Bachelier[a 10] puis Andreï Kolmogorov généraliseront cette propriété en 1936 pour les processus à temps continu.
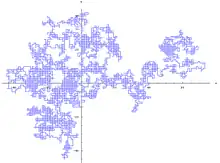
- Marches aléatoires
L'origine des marches aléatoires semble être attribuée au lord John William Strutt Rayleigh et son article de 1880 intitulé Composition of n isoperiodic vibrations of unit amplitude and of phases distributed at random. Le premier ouvrage sur les marches aléatoires isotropes est celui de Karl Pearson en 1905 sur les random flights (vols aléatoires en français). Vient alors le traité de George Pólya de 1921 dans lequel il traite les questions essentielles : récurrence, transience, point multiple, etc. Les marches aléatoires et leurs propriétés ont été généralisées sur les groupes, citons les travaux de Nicholas Varopoulos en 1985. Les travaux de marches aléatoires sur les groupes et les graphes continuent encore aujourd'hui, citons les 264 références dont Woess fait mention dans un article de survol en 1994[a 10].
- Mouvement brownien et équations différentielles stochastiques

L'histoire de ce processus commence en 1828 par Robert Brown avec une observation d'un mouvement de particules en suspension dans un liquide[a 10]. Suivent plusieurs expérimentations de physiciens au XIXe siècle, pour arriver à une formalisation plus mathématique de ce phénomène en 1905 et 1906 par le physicien Albert Einstein dans trois articles fondateurs dont un des buts était une évaluation du nombre d'Avogadro. À la même époque, Marian Smoluchowski publie une théorie du mouvement brownien tout à fait analogue. Le physicien Jean Perrin utilise les travaux d'Einstein pour estimer le nombre d'Avogadro ce qui lui valut le prix Nobel de physique en 1926. D'autre part le chimiste Theodor Svedberg reçut le prix Nobel de chimie en 1926 pour son exploitation de la formule de Smoluchowski.
Le premier mathématicien à avoir construit le mouvement brownien (ou plutôt le processus de Wiener) est Norbert Wiener en 1923 avec l'article Differential space dans lequel il construit une mesure sur l'espace des fonctions continues telle que ses accroissements sur des intervalles de temps disjoints suivent une loi normale prévue par la théorie d'Einstein. D'autre part, Paul Langevin relit les approches de Smoluchowski et d'Einstein en 1908 ; ses travaux seront formalisés mathématiquement en 1942 par Joseph Leo Doob. C'est le début des équations différentielles stochastiques (EDS). Une autre approche des EDS vient de Kiyoshi Itō dans cette même année 1942, avec la formule d'Itô qui reprend les travaux de Kolmogorov sur les processus de Markov à temps continu[a 10].
Les propriétés de ce processus sont étudiées par plusieurs auteurs telles que la non-dérivabilité en tout point du processus de Wiener, le Théorème de Paley-Wiener, la série de Fourier-Wiener par Raymond Paley, Norbert Wiener et Antoni Zygmund en 1933. Ces études sont basées sur la construction par Hugo Steinhaus, autour de 1930, des probabilités utilisant la mesure de Lebesgue sur l'intervalle [0,1] ou sur l'axiomatique de Andreï Kolmogorov faite en 1933[a 10].
L'étape suivante est le premier grand ouvrage sur le mouvement brownien écrit par Paul Lévy en 1948 et intitulé : processus stochastiques et mouvement brownien[a 10]. Il y fait mention, par exemple, de la non-récurrence du mouvement brownien en dimension trois et supérieur. Le comportement asymptotique du mouvement brownien commence en 1950 avec les travaux d'Eugène Dynkine.
Les travaux sur le mouvement brownien continuent encore aujourd'hui et il serait impossible de citer tous les auteurs comme l'atteste la biographie de cinq cents auteurs dans le livre de Daniel Revuz et Marc Yor publié en 1994[a 10].
- Martingale
Les premières idées de martingale, c'est-à-dire d'un processus vérifiant une propriété d'espérance conditionnelle, viennent des jeux de hasard avec les travaux de Pascal sur le problème des partis. Le terme martingale apparait pour la première fois dans la thèse de Jean Ville publiée en 1939 dans laquelle apparait l'expression : « système de jeu ou martingale ». Cette dénomination a été reprise par un de ses rapporteurs de thèse Joseph Leo Doob qui l'utilisa dans son ouvrage Stochastic processes publié en 1953. C'est ainsi au début du XXe siècle que les martingales sont formalisées mathématiquement avec les travaux de Bernstein, Ville, Borel et Doob. Notons également que John Hammersley exposa en 1967 une étude de processus stochastiques avec une propriété proche des martingales. Ce type de processus de Markov est particulièrement utilisé en mathématiques financières[a 11].

- Percolation
Le premier exemple de percolation a été publié par S. Broadbent en 1954, puis par S. Broadbent et John Hammersley en 1957 dans Percolation processes. I. Crystals and mazes comme un modèle de diffusion d'un fluide (liquide ou gaz) dans un milieu aléatoire[43]. Le milieu est composé aléatoirement de canaux ouverts ou fermés, ce qui a donné l'idée à Broadbent et Hammersley de donner le nom de percolation. En 1960, Ted Harris donne une estimation de la valeur critique, dans le réseau plan , d'obtenir une percolation (composante connexe de taille infinie)[44]. En 1980, Harry Kesten calcule cette valeur critique. Citons également Stanislav Smirnov qui obtint en 2010 la prestigieuse médaille Fields pour son travail dans ce domaine[a 12].
Applications
- Mathématiques financières
L'approche des processus stochastiques et du mouvement brownien (voir ci-dessus) faite par Bachelier, et l'utilisation de la formule d'Itô est particulièrement utilisée en mathématiques financières notamment avec le modèle Black-Scholes pour les prix d'options d'achats ou de ventes à des dates et prix donnés[a 10].
- Théorie de l'information
Claude Shannon et Norbert Wiener définissent, indépendamment, en 1948 une nouvelle définition de la quantité d'information dans le domaine de l'ingénierie des communications grâce à des méthodes probabilistes. Shannon montre que le nombre de messages produits par une source est fonction d'une quantité dénommée l'entropie de Shannon, sous les conseils de John von Neumann. Wiener utilise pour sa part une partie de la statistique via les séries temporelles pour considérer un domaine plus vaste que la théorie de l'information et du traitement du signal : la physique statistique. Cette approche amène, dans les années 1960, un renversement qui propose d'utiliser la théorie de l'information pour redéfinir des notions probabilistes[a 13].
Lois de probabilité
Certaines lois de probabilité ont été définies initialement comme le résultat statistique d'une expérience ou comme le comportement asymptotique d'autres lois, elles ont par la suite été définies rigoureusement.
- Loi de Cauchy
Une courbe proportionnelle à apparait pour la première au milieu du XVIIe siècle dans les travaux de Pierre de Fermat. Elle a alors été étudiée par plusieurs auteurs tels que Newton, Leibniz, Huygens, Guido Grandi et Agnesi ; ainsi au XIXe siècle la courbe prend le nom de sorcière d'Agnesi. Poisson publia un article en 1824 dans lequel il utilise la densité de la loi de Cauchy comme contre-exemple de certains résultats de Laplace. Quelques années plus tard, le nom d'Augustin Louis Cauchy a été associé à cette loi à la suite d'une dispute mathématique entre Cauchy et Irénée-Jules Bienaymé qui fut brève (2 mois de 1853) mais intense. Le débat portait sur une nouvelle méthode d'interpolation de Cauchy différente de la méthode des moindres carrés ; dans son argumentation Cauchy proposa la densité de la loi de Cauchy. Il est possible que Cauchy n'ait pas été familier des travaux de Poisson, bien que ses contemporains les mentionnent, Bienaymé par exemple[a 14].
- Loi du χ²
Tandis qu'en 1838, Irénée-Jules Bienaymé obtient la loi du χ² comme limite de variables aléatoires discrètes de loi multinomiale, La formulation de cette loi du chi-carré est due au physicien Ernst Abbe en 1863, selon le statisticien Oscar Sheynin[45]. Ludwig Boltzmann en présenta le cas général en 1881. C'est en 1900 que Karl Pearson utilise cette loi en statistique comme approximation dans les tests statistiques[45].
- Loi gamma
La loi gamma est issue des travaux de Pierre-Simon de Laplace en 1838[46].
- Loi normale
Une des premières apparitions de la loi normale est due[a 15] à Abraham de Moivre en 1733 en approfondissant l'étude de la factorielle lors de l'étude d'un jeu de pile ou face. Il publie The doctrine of chances en 1756 dans lequel la loi normale apparaît comme limite d'une loi binomiale, ce qui sera à l'origine du théorème central limite[a 16]. En 1777, Pierre-Simon de Laplace reprend ces travaux et obtient une bonne approximation de l'erreur entre cette loi normale et la loi binomiale grâce à la Fonction Gamma d'Euler[a 15]. Dans son ouvrage publié en 1781, Laplace donne une première table de cette loi. En 1809, Carl Friedrich Gauss assimile des erreurs d'observation en astronomie à la courbe, dite des erreurs, de la densité de la loi normale[a 16].
La loi normale est alors pleinement définie lorsque le premier théorème central limite, alors appelé théorème de Laplace, est énoncé par Laplace en 1812[a 15]. Son nom « normale » est donné par Henri Poincaré à la fin du XIXe siècle[47]. La loi porte également le nom loi de Gauss ou loi de Laplace-Gauss[48] en fonction de l'attribution de la paternité de la création de cette loi.
La loi normale est toujours une loi étudiée. Par exemple, de nouvelles tables numériques sont données en 1948 par Egon Sharpe Pearson, en 1952 par le National Bureau of Standards et en 1958 par Greenwood et Hartley[49].
- Loi uniforme
La loi uniforme (discrète) apparait vraisemblablement pour la première fois dans la thèse de doctorat de Nicolas Bernoulli publiée en 1711[9].
Enseignement
Bien que des recherches et des réflexions sur les probabilités existent depuis longtemps (voir Histoire des probabilités), le premier cours systématique de calcul des probabilités dispensé en France l'a été en 1786 par Sylvestre-François Lacroix alors âgé de 21 ans. Il enseigne alors pendant une année au Lycée sous la demande et la supervision de Nicolas de Condorcet. Ce dernier s'occupe de traduire les œuvres de Leonhard Euler et ajoute un volume consacré aux calcul des probabilités intitulé : Elemens du calcul des probabilités et son application aux jeux de hasard, à la loterie, et au jugemens des hommes publié à titre posthume en 1805[50]. Les probabilités y sont énoncées de manière non formelle et en utilisant la langue naturelle[51].
En 1795[a 17], Pierre-Simon de Laplace enseigne à l'école normale, Joseph Fourier y assiste[52]. Plus tard en 1797, Fourier enseigne les probabilités aux deuxièmes et troisièmes années de l'école polytechnique, Siméon Denis Poisson y est étudiant[a 17]. Le programme du cours de Fourier est complet et méthodique, il traite de l'aspect mathématique et des applications (voir ci-dessous).
| Règles | Mesure de la probabilité
Des événemens composés, calcul de leur probabilité Des chances multiples, calcul de leur probabilité | ||||||||||||||||||||||||||||||||||
| Remarques | Sur la probabilité des témoignages
Sur les exclusions par le sort et l’ordre des tirages Sur les loteries, le calcul des diverses chances et les fausses espérances des joueurs Sur les jeux de dés et l’influence des inégalités inconnues dans la constitution de l’évaluation commune de la somme espérée Remarques sur l’inexactitude de cette règle | ||||||||||||||||||||||||||||||||||
| Applications aux jeux de hasard | De l’analyse exacte des jeux de hasard
Du jeu qui finit avec l’argent des joueurs Du jeu du franc carreau De quelques autres jeux de hasard De l’avantage que présente la chance des nombres impairs De la probabilité d’amener un événement donné d’un certain nombre de faits au moins en un nombre de coups proposé Remarque sur l’influence de l’avantage du jeu | ||||||||||||||||||||||||||||||||||
| Applications diverses | De la valeur morale de l’argent et de la juste évaluation des sommes espérées
Du désavantage qui résulte de tous les jeux de hasard De l’avantage mutuel de certaines transactions et en particulier des assurances De l’avantage qu’il y a de diviser les sommes hazardées Du bien que procure un don et de l’utilité de diviser les dons Du problème de Petersbourg Remarques sur l’égalité possible de toutes les chances, les jugemens divers et les illusions des joueurs | ||||||||||||||||||||||||||||||||||
| Des décisions des assemblées | Des élections ; des différentes modes d’élection. Du scrutin individuel et du scrutin de liste.
Remarques sur les imperfections de la plupart des modes De la probabilité des décisions en général, application à la composition des tribunaux Du choix d’un nombre par une assemblée Du choix entre plusieurs questions | ||||||||||||||||||||||||||||||||||
| Méthode inverse des probabilités. Règles | De la probabilité des causes prise des événemens, mesure de cette probabilité
De la probabilité des événemens futurs dont les causes sont ignorées De la probabilité des événemens prise des événemens observés Remarques analytiques sur le calcul des fonctions de très grands nombres Des cas où les événemens observés indiquent les causes avec beaucoup de vraisemblance | ||||||||||||||||||||||||||||||||||
| Des hypothèses physiques | De la vraisemblance des hypothèses physiques
Application au principe de la gravitation universelle…, à l’explication du flux et du reflux…, à la pesanteur de l’air…, et aux causes qui ont pu déterminer le mouvement commun des planètes | ||||||||||||||||||||||||||||||||||
| Application du calcul à l’histoire naturelle de l’homme | Application des règles précédentes à l’histoire naturelle de l’homme
Des tables de mortalité… des naissances… des mariages etc. De la population, du rapport du nombre des naissances annuelles à la population De la durée de la vie moyenne et de ses valeurs successives De la probabilité d’atteindre un âge donné Du rapport du nombre de mariages au nombre d’enfants Du calcul de la population de la France De l’inégalité des naissances des garçons et des filles De l’extrême vraisemblance des causes de cette inégalité De l’inégalité de ces causes dans plusieurs climats d’Europe | ||||||||||||||||||||||||||||||||||
| Des rentes viagères, assurances, tontines etc. | Des rentes viagères, règles pour les calculer
Des rentes sur deux têtes, sur trois têtes, etc. Des tontines simples, des tontines composées Des assurances et de leur calcul dans les différens cas, des caisses d’épargne, mont de piété, etc. Des droits éventuels…. contrats aléatoires… etc. | ||||||||||||||||||||||||||||||||||
| De l’inoculation | Théorie mathématique de l’inoculation, et des avantages généraux de cette pratique | ||||||||||||||||||||||||||||||||||
| Calcul des observations | Du calcul des résultats moyens de plusieurs observations
De la correction des instrumens | ||||||||||||||||||||||||||||||||||
| Réflexions sur le calcul des probabilités | Vues générales sur les applications du calcul des probabilités, des erreurs auxquelles elles ont exposé
De l’histoire de cette science, tableau des auteurs qui en ont traité (voyez page suivante) Conclusion | ||||||||||||||||||||||||||||||||||
| Notice des auteurs qui ont traité du calcul des probabilités |
|
Une chaire de probabilité à la faculté des sciences de Paris est ouverte en 1834 sous la demande de Poisson. Cette place sera occupée par Guillaume Libri, mais ce dernier se fait souvent remplacer notamment par Poisson[53].
Une grande avancée de l'enseignement des probabilités en France se déroule en 1922 lors de la création de l'ISUP[a 18]. Par la volonté d'Émile Borel, de Lucien March et entre autres de Fernand Faure, des cours de probabilité sont donnés à partir de 1924 à la faculté de droit et à l'institut Henri-Poincaré, suivis notamment par des étudiants de l'ENS et de l'école polytechnique. Les cours sont assurés par Borel, Georges Darmois ou Daniel Schwartz[a 18].
En 2008, le choix a été fait de commencer à enseigner les probabilités dès les classes de collège[a 19]. Le but est de donner une initiation aux probabilités (et à la statistique) aux élèves afin de former au langage, aux concepts et de déceler les questions de nature statistique.
Recherche
Bien que la théorie des probabilités soit une théorie récente, la recherche y est particulièrement active. Plusieurs laboratoires de recherche se sont créés, citons par exemple le cas du laboratoire de probabilités et modèles aléatoires, rattaché aux universités parisiennes Pierre-et-Marie-Curie (Paris 6) et Diderot (Paris 7), qui fut créé en 1960 à l'initiative de Robert Fortet par le CNRS[a 20].
De nombreux séminaires et colloques en probabilité sont organisés. Pour la France, outre les séminaires des laboratoires, citons l'école d'été de probabilité de Saint-Flour qui existe depuis 1971[a 21], les journées MAS[a 22] ou les journées de probabilité[a 23].
Plusieurs prix sont donnés aux mathématiciens pour mettre en valeur leur recherche, certains d'entre eux sont réservés aux probabilistes. C'est le cas du prix Rollo Davidson par exemple. Il est à noter que le plus prestigieux prix de mathématique, c'est-à-dire la médaille Fields, a été décernée pour la première fois à un probabiliste en 2006, à savoir Wendelin Werner[a 24].
Il existe une classification des domaines de recherche en mathématique appelée Mathematics Subject Classification et utilisée par les bases de données Mathematical Reviews et Zentralblatt MATH[a 25]. La classe 60 concerne la théorie des probabilités et les processus stochastiques.
Références
Ouvrages
- Henry 2001, p. 13
- Henry 2001, p. 14
- Dodge 2004, p. 409
- Dalang et Conus 2008, p. 127
- Henry 2001, p. 17
- Dodge 2004, p. 247
- Henry 2001, p. 25
- Henry 2001, p. 19
- Dalang et Conus 2008, p. 128
- Courtebras 2006, p. 15
- Henry 2001, p. 18
- Henry 2001, p. 24
- Henry 2001, p. 32
- Henry 2001, p. 34
- Henry 2001, p. 43
- Henry 2001, p. 42
- Henry 2001, p. 38
- Dale 1999, p. 5
- Dale 1999, p. 4
- Dale 1999, p. 170
- Dale 1999, p. 171
- Dale 1999, p. 173
- Tassi et Legait 1990, p. 33
- Courtebras 2006, p. 28
- Courtebras 2006, p. 6
- Courtebras 2006, p. 33
- Courtebras 2006, p. 57
- Courtebras 2006, p. 64
- Courtebras 2006, p. 13
- Tassi et Legait 1990, p. 34
- Klein et Sacquin 1998, p. 67
- Klein et Sacquin 1998, p. 68
- Klein et Sacquin 1998, p. 70
- Klein et Sacquin 1998, p. 69
- Courtebras 2006, p. 76
- Fisher 2010, p. 15
- Fisher 2010, p. 22
- Fisher 2010, p. 23
- Fisher 2010, p. 4
- Fisher 2010, p. 5
- Fisher 2010, p. 1
- Dodge 2004, p. 413
- Kesten 1982, p. 1
- Kesten 1982, p. 2
- Dodge 2004, p. 300
- Dodge 2004, p. 302
- Stigler 1999, p. 407
- Stigler 1999, p. 406
- Dodge 2004, p. 502
- Courtebras 2006, p. 25
- Courtebras 2006, p. 31
- Courtebras 2006, p. 46
- Courtebras 2006, p. 65
Autres œuvres
- étude philosophique sur Aristote
- analyse du sens de "probabilité" au XVIe siècle dans les commentaires des Topiques
- voir l'entrée probabilité du dictionnaire TLFI
- http://www.jehps.net/Juin2007/Ceccarelli_Risk.pdf, Journ@l Électronique d’Histoire des Probabilités et de la Statistique
- http://www.jehps.net/Juin2007/Piron_incertitude.pdf, Journ@l Électronique d’Histoire des Probabilités et de la Statistique
- Catholic encyclopeida, 1911, article sur le probabilisme.
- un site sur la pensée de Pascal.
- Entre De Moivre et Laplace
- DicoMaths : Chaine de Markov
- Jean-Pierre Kahane, « Le mouvement brownien », Société mathématique de France, , p. 123-155 (lire en ligne)
- Roger Mansuy, « HISTOIRE DE MARTINGALES », Mathematical Social Sciences, vol. 169, no 1, , p. 105-113 (lire en ligne)
- (en) Thomas Liggett, « T. E. Harris’ contributions to interacting particle systems and percolation », The Annals of Probability, vol. 39, no 2, , p. 407-416 (lire en ligne)
- Mathieu Triclot, « Information et entropie. Un double jeu avec les probabilités. », jehps, vol. 3, no 2, (lire en ligne)
- (en) Stephen Stigler, « Cauchy and the witch of Agnesi », Studies in the History of Probability and Statistics XXXIII, vol. 61, no 2, , p. 375 (lire en ligne)
- Bernard Bru, « La courbe de Gauss ou le théorème de Bernoulli raconté aux enfants », Mathematics and Social Sciences, vol. 175, no 3, , p. 5-23 (lire en ligne)
- Aimé Fuchs, « Plaidoyer pour la loi normale », Pour la Science, , p. 17 (lire en ligne)
- Pierre Crepel, « De Condorcet à Arago : l’enseignement des probabilités en France de 1786 à 1830 », Bulletin de la SABIX, vol. 4, , p. 29-55 (lire en ligne)
- Norbert Meusnier, « Sur l'histoire de l'enseignement des probabilités et des statistiques », Journal électronique d'histoire des probabilités et de la statistique, vol. 2, no 2, (lire en ligne)
- « ressource pour les classes de collège - Mathématiques - Probabilités », sur éduscol,
- « Le LPMA fête ses 50 ans », sur Fondation sciences mathématiques de Paris
- « Ecole d'été de Saint-Flour », sur labotratoire de Math. de Clermont-Ferrand
- « Journées MAS », sur smai
- « journées de probabilité », sur laboratoire de Math. de l'université d'Orléans,
- « Historique », sur département de mathématiques et applications - école normale supérieure
- (en) « 2000 Mathematics Subject Classification », sur ams
Voir aussi
Bibliographie
- Bernard Courtebras, À l'école des probabilités : une histoire de l'enseignement français du calcul des probabilités, Besançon, Presses universitaires de Franche-Comté, , 285 p. (ISBN 2-84867-110-6, lire en ligne).

- Bernard Courtebras, Mathématiser le hasard, Vuibert,
- Dalang et Conus, Introduction à la théorie des probabilités, Lausanne, Presses polytechniques et universitaires romandes, , 204 p. (ISBN 978-2-88074-794-7, lire en ligne).

- Yadolah Dodge, Statistique : dictionnaire encyclopédique, Paris/Berlin/New York etc., Springer, , 2e éd., 637 p. (ISBN 2-287-21325-2, lire en ligne).

- (en) Andrew Dale, A history of inverse probability : from Thomas Bayes to Karl Pearson, New York, Springer, , 679 p. (ISBN 0-387-98807-6, lire en ligne).

- (en) Hans Fisher, A History of the Central Limit Theorem, Springer, , 402 p. (ISBN 978-0-387-87856-0, lire en ligne).

- Étienne Klein et Yves Sacquin (dir.), Prédiction & Probabilité dans les sciences, Éditions frontières, , 159 p. (ISBN 2-86332-232-X, lire en ligne).

- (en) Harry Kesten, Percolation Theory for Mathematicians, Birkhäuser, (lire en ligne).

- Michel Henry, Probabilités et statistique, Presses Universitaires de Franche-Comté, , 262 p. (lire en ligne).

- Ph. Tassi et S. Legait, Théorie des probabilités, Paris/Rueil-Malmaison, Technip, , 367 p. (ISBN 2-7108-0582-0, lire en ligne).

- (en) Stephen Stigler, Statistics on the table : the history of statistical concepts and methods, Cambridge (Mass.)/London, Harvard University Press, , 499 p. (ISBN 0-674-83601-4, lire en ligne).




![{\displaystyle Pr[C_{i}|E]=Pr[E|C_{i}]Pr[C_{i}]{\big /}\sum _{j}Pr[E|C_{j}]Pr[C_{j}]}](https://img.franco.wiki/i/f17351d90b1e3cd6975d7e40e2571700f5d5d2aa.svg)














