SL₂(R)

Le groupe SL(2, R) est le groupe de toutes les transformations linéaires bijectives de R² qui préservent l'aire orientée. Il est isomorphe au groupe symplectique Sp(2, R) et au groupe spécial unitaire SU(1, 1). Il est également isomorphe au groupe des coquaternions de norme 1. Le groupe SL^±(2, R) préserve l'aire non orientée : ses éléments peuvent inverser l'orientation.

Le quotient PSL(2, R) admet plusieurs descriptions intéressantes :

• c'est le groupe des transformations projectives qui préservent l'orientation de la droite projective réelle R ∪ {∞} ;
• c'est le groupe des automorphismes conformes du disque unité ;
• c'est le groupe des isométries préservant l'orientation du plan hyperbolique ;
• c'est le groupe de Lorentz restreint de l'espace de Minkowski de dimension trois ; de manière équivalente, il est isomorphe au groupe orthogonal SO⁺(1, 2) de la forme de signature (1, 2) ; il s'ensuit que SL(2, R) est isomorphe au groupe spinoriel Spin(2,1)⁺.

Les éléments du groupe modulaire PSL(2, Z) ont des interprétations supplémentaires, de même que les éléments du groupe SL(2, Z) (en tant que transformées linéaires du tore), et ces interprétations peuvent également être vues à la lumière de la théorie générale de SL(2, R).

Spectre

Une valeur propre ${\displaystyle \lambda }$ d'un élément A ∈ SL(2, R) est une racine du polynôme caractéristique

${\displaystyle \lambda ^{2}\,-\,\mathrm {tr} (A)\,\lambda \,+\,1}$

de sorte que

${\displaystyle \lambda ={\frac {\mathrm {tr} (A)\pm {\sqrt {\mathrm {tr} (A)^{2}-4}}}{2}}.}$

Cela conduit à la classification suivante des éléments, avec une description correspondante de leur action sur le plan euclidien :

• si |tr(A)| < 2, alors A est dit elliptique et est conjugué à une rotation (les valeurs propres sont complexes conjuguées) ;
• si |tr(A)| = 2, alors A est appelé parabolique, et est une transvection (il y a une valeur propre double, égale à ± 1) ;
• si |tr(A)| > 2, alors A est appelé hyperbolique, et est une rotation hyperbolique (les valeurs propres sont réelles, inverses l'une de l'autre).

Les noms correspondent à la classification des coniques selon leur excentricité : si l'on définit l'excentricité comme la moitié de la valeur absolue de la trace (ε = ½ tr ; diviser par 2 tient compte de la dimension, alors que la valeur absolue correspond à travailler au signe près comme si l'on était dans PSL(2,R)), on obtient la correspondance suivante : ${\displaystyle \epsilon <1}$, elliptique ; ${\displaystyle \epsilon =1}$, parabolique ; ${\displaystyle \epsilon >1}$, hyperbolique.

L'élément neutre I et son opposé −I (dans PSL(2, R) ils sont identifiés), ont une trace ±2, et sont donc des éléments paraboliques d'après la classification précédente, bien qu'ils soient souvent considérés à part.

La même classification est utilisée pour SL(2, C) mais aussi, puisque la trace d'un élément du groupe projectif est définie au signe près et que la classification ne tient compte que du module de la trace, pour PSL(2, C) (transformations de Möbius) et PSL(2, R) (transformations de Möbius réelles). Dans les groupes complexes, on trouve en plus des transformations dites loxodromiques lorsque la trace est complexe. Il existe des classifications analogues (en) par une notion d'excentricité.

Un sous-groupe qui ne contient que des éléments elliptiques (respectivement paraboliques, hyperboliques), en plus de l'identité et de son opposée, est appelé un sous-groupe elliptique (respectivement sous-groupe parabolique, sous-groupe hyperbolique).

Il s'agit d'une classification en sous-ensembles et non en sous-groupes : ces ensembles ne sont pas stables par multiplication (le produit de deux éléments paraboliques n'est pas toujours parabolique, etc.). Cependant, tout élément est conjugué à un élément de l'un de trois sous-groupes à un paramètre standards (éventuellement au signe près), comme détaillé ci-dessous.

Topologiquement, comme la trace est une application continue, les éléments elliptiques (en excluant ±I) forment un ensemble ouvert, tout comme les éléments hyperboliques (en excluant ±I), tandis que les éléments paraboliques (en incluant ±I) sont un ensemble fermé.

La décomposition d'Iwasawa d'un groupe est une méthode pour présenter le groupe comme un produit de trois sous-groupes de Lie K, A, N. Pour ${\displaystyle {\mbox{SL}}(2,\mathbf {R} )}$ ces trois sous-groupes sont

${\displaystyle K=\left\{{\begin{pmatrix}\cos \theta &-\sin \theta \\\sin \theta &\cos \theta \end{pmatrix}}\in \operatorname {SL} (2,\mathbb {R} )\ |\ \theta \in \mathbf {R} \right\}\cong \operatorname {SO} (2),}$

${\displaystyle A=\left\{{\begin{pmatrix}r&0\\0&r^{-1}\end{pmatrix}}\in \operatorname {SL} (2,\mathbb {R} )\ |\ r>0\right\},}$

${\displaystyle N=\left\{{\begin{pmatrix}1&x\\0&1\end{pmatrix}}\in \operatorname {SL} (2,\mathbb {R} )\ |\ x\in \mathbf {R} \right\}.}$

L'énoncé précis exprime que l'application produit

${\displaystyle {\begin{array}{rcl}K\times A\times N&\longrightarrow &\operatorname {SL} (2,\mathbb {R} )\\(k,a,n)&\longmapsto &kan\end{array}}}$

est un homéomorphisme (mais bien sûr pas un morphisme de groupes).

Les groupes K, A et N contiennent respectivement les formes normales pour les sous-ensembles elliptique, hyperbolique et parabolique.

Comme espace topologique, PSL(2, R) peut être décrit comme le fibré tangent unitaire du plan hyperbolique. C'est un fibré en cercles (en), il a une structure de contact naturelle induite par la structure symplectique sur le plan hyperbolique. Quant à SL(2, R), c'est un revêtement double de PSL(2, R), il peut être considéré comme le fibré des spineurs sur le plan hyperbolique.

Le groupe fondamental de SL(2, R) est le groupe monogène infini Z. Le revêtement universel, noté ${\displaystyle {\overline {{\mbox{SL}}(2,\mathbf {R} )}}}$, est un exemple de groupe de Lie de dimension finie qui n'est pas un groupe de matrices. Autrement dit, ${\displaystyle {\overline {{\mbox{SL}}(2,\mathbf {R} )}}}$ n'admet aucune représentation fidèle de dimension finie.

En tant qu'espace topologique, ${\displaystyle {\overline {{\mbox{SL}}(2,\mathbf {R} )}}}$ est un fibré en droites sur le plan hyperbolique. Lorsqu'il est muni d'une métrique invariante à gauche, la 3-variété ${\displaystyle {\overline {{\mbox{SL}}(2,\mathbf {R} )}}}$ devient l'une des huit géométries de Thurston. Par exemple, ${\displaystyle {\overline {{\mbox{SL}}(2,\mathbf {R} )}}}$ est la couverture universelle du fibré tangent unitaire de toute surface de Riemann hyperbolique. Toute variété modelée sur ${\displaystyle {\overline {{\mbox{SL}}(2,\mathbf {R} )}}}$ est orientable et c'est un fibré en cercles sur une orbifold hyperbolique de dimension deux (un fibré de Seifert).

Le groupe de tresses B₃ est l'extension centrale universelle du groupe modulaire.

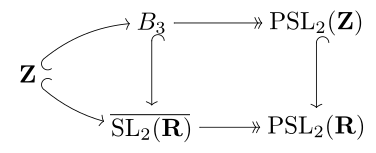
L'image réciproque par ce revêtement du groupe modulaire PSL(2, Z) est le groupe de tresses sur 3 brins, B₃, qui est l'extension centrale universelle du groupe modulaire. Ces groupes sont des réseaux de groupes algébriques convenables et cela correspond algébriquement au revêtement universel en topologie.

Le groupe de revêtement double peut être identifié au groupe métaplectique Mp(2, R), quand on considère SL(2, R) comme le groupe symplectique Sp(2, R).

Les groupes mentionnés ci-dessus peuvent être mis ensemble dans un complexe :

${\displaystyle {\overline {\mathrm {SL} (2,\mathbf {R} )}}\to \cdots \to \mathrm {Mp} (2,\mathbf {R} )\to \mathrm {SL} (2,\mathbf {R} )\to \mathrm {PSL} (2,\mathbf {R} ).}$

Il existe d'autres revêtements de PSL(2, R). Plus précisément, il y en a un pour chaque entier naturel n car nZ est un sous-groupe de Z ≅ π₁(PSL(2, R)). Ces groupes forment un treillis de groupes de revêtement ordonné par la divisibilité ; le groupe correspondant à n est un revêtement de SL(2, R) si et seulement si n est pair.

Le centre de SL(2, R) est le groupe à deux éléments {±I} et le quotient PSL(2, R) est simple.

Les sous-groupes discrets de PSL(2, R) sont appelés groupes fuchsiens (en). Ils sont l'analogue hyperbolique des groupes de papier peint euclidiens et des groupes de frises. Le plus célèbre d'entre eux est le groupe modulaire PSL(2, Z), qui agit sur un pavage du plan hyperbolique par des triangles idéaux.

Le groupe du cercle SO(2) est un sous-groupe compact maximal de SL(2, R), et le cercle SO(2) / {±I} est un sous-groupe compact maximal de PSL(2, R).

Le multiplicateur de Schur du groupe discret PSL(2, R) est beaucoup plus grand que Z et l'extension centrale universelle est beaucoup plus grande que le revêtement universel. Cependant ces grandes extensions centrales ne tiennent pas compte de la topologie et sont quelque peu pathologiques.

Le groupe SL(2, R ) est un groupe de Lie simple réel et non compact, c'est la forme réelle scindée du groupe de Lie complexe SL(2, C). L'algèbre de Lie de SL(2, R), noté sl(2, R), est l'algèbre de Lie de toutes les matrices 2 × 2 réelles de trace nulle. C'est l'algèbre de Bianchi de type VIII.

La théorie des représentations en dimension finie de SL(2, R) est équivalente à la théorie des représentations de SU(2), qui est la forme réelle compacte de SL(2, C). En particulier, SL(2, R) n'a pas de représentation unitaire de dimension finie non triviale. C'est une caractéristique de tous les groupes de Lie simples connexes non compacts. Pour un aperçu de la preuve, voir la non-unitarisabilité des représentations (en).

La théorie des représentations de dimension infinie de SL(2, R) est vraiment intéressante. Le groupe admet plusieurs familles de représentations unitaires, qui ont été étudiées en détail par Gelfand et Naimark (1946), V. Bargmann (1947) et Harish-Chandra (1952).