Chimie quantique relativiste

En 1935, Bertha Swirles décrit un traitement relativiste d’un système à plusieurs électrons[5], malgré l’affirmation de Paul Dirac en 1929 qui indiquait que les seules imperfections qui demeurent en mécanique quantique « n’entraînent de difficultés que lorsque des particules à grande vitesse sont impliquées, et sont donc sans importance dans la prise en compte de la structure atomique et moléculaire et les réactions chimiques ordinaires, lesquelles sont, en effet, généralement suffisamment précises si on néglige la variation relativiste de la masse et de la vitesse et qu’on suppose uniquement des forces coulombiennes entre les divers électrons et les noyaux atomiques[6]. »

Les chimistes théoriciens partageaient globalement l’opinion de Dirac jusque dans les années 1970, lorsque les effets relativistes commencèrent à être observés dans les éléments lourds[7]. Schrödinger établit l’équation qui porte son nom dans son article de 1926 sans tenir compte de la relativité[8]. Des corrections relativistes furent apportées à l’équation de Schrödinger (voir l’équation de Klein-Gordon) afin d’expliquer la structure fine des spectres atomiques, mais ce développement, ainsi que d’autres, ne percèrent pas immédiatement dans la communauté des chimistes. Comme les lignes spectrales atomiques relevaient en grande partie de la physique et non de la chimie, la majorité des chimistes n’étaient pas familiers avec la mécanique quantique relativiste, et leur attention portait sur des éléments plus légers typiques de l’intérêt pour la chimie organique à cette époque[9].

La vision de Dirac du rôle de la mécanique quantique relativiste dans les systèmes chimiques était erronée pour deux raisons : la première est que les électrons des orbitales atomiques s et p se déplacent à une fraction significative de la vitesse de la lumière ; la deuxième est qu’il y a des conséquences indirectes des effets relativistes qui sont particulièrement évidentes pour les orbitales atomiques d et f.

Le facteur de Lorentz γ en fonction de la vitesse. Pour une vitesse faible, ${\displaystyle E_{rel}}$ (ordonnée) est égal à ${\displaystyle E_{0}=mc^{2}}$ mais lorsque ${\displaystyle v_{e}\to c}$, ${\displaystyle E_{rel}}$ tend vers l’infini.

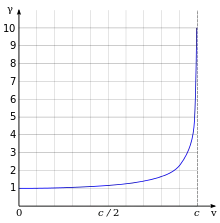
L’un des résultats les plus importants et les plus largement connus de la relativité est que la masse relativiste (en) de l’électron croît selon l’équation :

${\displaystyle m_{rel}={\frac {m_{e}}{\sqrt {1-(v_{e}/c)^{2}}}}}$,

où ${\displaystyle \displaystyle m_{e},v_{e},c}$ sont respectivement la masse au repos de l’électron, la vitesse de l’électron et la vitesse de la lumière. La figure de droite illustre les effets relativistes sur la masse d’un électron en fonction de sa vitesse.

Cela a une implication immédiate sur le rayon de Bohr (${\displaystyle \displaystyle a_{0}}$) qui est donné par :

${\displaystyle a_{0}={\frac {\hbar }{m_{e}c\alpha }}}$

où ${\displaystyle \hbar }$ est la constante de Planck réduite et α est la constante de structure fine (une correction relativiste du modèle de Bohr).

Arnold Sommerfeld a calculé que, pour un électron 1s de l’atome d’hydrogène ayant un rayon orbital de 52,9 pm, α ≈ ¹⁄₁₃₇. C’est-à-dire que la constante de structure fine montre un électron voyageant à environ ¹⁄_137^e de la vitesse de la lumière[10]. On peut étendre cela à un élément plus lourd en utilisant l’expression v ≈ ^Z⁄₁₃₇c pour un électron 1s, où v est sa vitesse radiale. Pour l’or, avec Z = 79, l’électron 1s se déplace ainsi à 58 % de la vitesse de la lumière, puisque ⁷⁹⁄₁₃₇ ≈ 0,58. En reliant cela à la masse relativiste, on trouve que m_rel = 1,22m_e et en l’injectant dans le rayon de Bohr ci-dessus, on trouve que le rayon diminue de 22 %.

Si l’on substitue la masse relativiste dans l’équation donnant le rayon de Bohr, on obtient :

${\displaystyle a_{rel}={\frac {\hbar {\sqrt {1-(v_{e}/c)^{2}}}}{m_{e}c\alpha }}}$

Rapport des rayons de Bohr relativiste et non relativiste en fonction de la vitesse de l’électron.

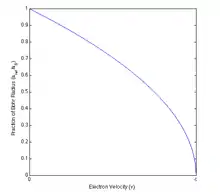
Il s’ensuit que :

${\displaystyle {\frac {a_{rel}}{a_{0}}}={\sqrt {1-(v_{e}/c)^{2}}}}$

À droite, le rapport ci-dessus des rayons de Bohr relativiste et non-relativiste a été tracé en fonction de la vitesse de l’électron. On remarque que le modèle relativiste montre que le rayon diminue lorsque la vitesse augmente.

Lorsque le traitement de Bohr est étendu aux atomes hydrogénoïdes en utilisant la règle quantique, le rayon de Bohr devient :

${\displaystyle r={\frac {n^{2}\hbar ^{2}4\pi \epsilon _{0}}{m_{e}Ze^{2}}}}$

où ${\displaystyle n}$ est le nombre quantique principal et Z est un entier représentant le numéro atomique. D’après la mécanique quantique, le moment angulaire est donné par ${\displaystyle mv_{e}r=n\hbar }$. En remplaçant dans l’équation ci-dessus et résolvant pour ${\displaystyle v}$, on obtient :

${\displaystyle r={\frac {mv_{e}rn\hbar 4\pi \epsilon _{0}}{mZe^{2}}}}$

${\displaystyle 1={\frac {v_{e}n\hbar 4\pi \epsilon _{0}}{Ze^{2}}}}$

${\displaystyle v_{e}={\frac {Ze^{2}}{n\hbar 4\pi \epsilon _{0}}}}$

À partir d’ici, le système d’unités atomiques peut être utilisé pour simplifier l’expression en :

${\displaystyle v_{e}={\frac {Z}{n}}}$

En remplaçant cela dans l’expression donnant le rapport de Bohr mentionné ci-dessus, on obtient :

${\displaystyle {\frac {a_{rel}}{a_{0}}}={\sqrt {1-\left({\frac {Z}{nc}}\right)^{2}}}}$

On peut remarquer à présent que, pour une valeur de ${\displaystyle n}$ faible et une valeur de ${\displaystyle Z}$ élevée, le rapport ${\displaystyle {\frac {a_{rel}}{a_{0}}}}$ est inférieur à 1. Cela est conforme à l’intuition : les électrons ayant un nombre quantique principal plus petit auront une densité de probabilité plus grande d’être plus proche du noyau. Un noyau ayant une charge électrique élevée sera entouré d’électrons ayant une vitesse élevée. Des électrons rapides ont une masse relativiste élevée et passeront donc plus de temps à proximité du noyau, ce qui fait que le rayon se contracte pour les nombres quantiques principaux les plus petits[11].

Le tableau périodique des éléments a été construit par des scientifiques qui avaient observé que les propriétés des éléments chimiques connus à leur époque avaient tendance à évoluer de manière périodique en fonction de leur masse atomique, puis, de façon plus exacte, de leur numéro atomique. Ils ont organisé ces éléments sous la forme d’un tableau qui rend compte de ces périodicités, ce qui donne au tableau périodique toute sa pertinence. De nombreuses différences chimiques et physiques entre éléments de la sixième période (Cs–Rn) et de la cinquième période (Rb–Xe) proviennent d’effets relativistes sensibles pour la période 6, alors qu’ils sont négligeables pour la période 5. Ces effets relativistes sont particulièrement significatifs pour l’or et ses voisins, le platine et le mercure.

Couleur de l’or et du césium

Courbes de réflectance spectrale pour des miroirs de métal en aluminium (Al), en argent (Ag) et en or (Au).

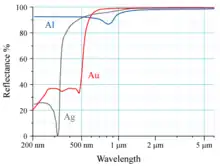
La réflectivité de l’or Au, de l’argent Ag et de l’aluminium Al est représentée sur la figure à droite. L’œil humain perçoit le rayonnement électromagnétique ayant une longueur d’onde proche de 600 nm comme du jaune. Comme on le voit à partir de ce spectre de réflectance, l’or paraît jaune parce qu’il absorbe la lumière bleue plus qu’il n’absorbe les autres longueurs d’onde visibles de la lumière ; la lumière réfléchie, qui est celle que nous percevons, est donc dépourvue de bleu par rapport à la lumière incidente. Puisque le jaune est complémentaire du bleu, cela se traduit par le fait qu’un morceau d’or semble jaune (sous une lumière blanche) aux yeux humains.

La transition électronique responsable de cette absorption est une transition du niveau d’énergie 5d au niveau 6s. Une transition semblable se produit dans l’argent, mais les effets relativistes sont plus faibles dans cet élément, de sorte que le niveau 4d y connaît une certaine expansion et le niveau 5s une certaine contraction, l’écart 4d-5s dans l’argent étant de ce fait bien plus grand que l’écart 5d-6s dans l’or en raison d’effets relativistes moindres dans l’argent que ceux observés dans l’or. Ainsi, l’or non-relativiste serait blanc. Les effets relativistes élèvent le niveau de l’orbitale 5d et abaissent le niveau de l’orbitale 6s[12].

Césium dans une ampoule.

Un effet semblable se produit dans le césium, le plus lourd des métaux alcalins pouvant être observé (le francium est trop radioactif pour pouvoir former des masses de matière macroscopique). Alors que les autres métaux alcalins sont blanc argenté, le césium présente une teinte nettement dorée.

Sans la relativité, le plomb devrait se comporter comme l’étain, de sorte que les batteries étain-acide devraient fonctionner aussi bien que les batteries plomb-acide couramment utilisées dans les voitures. Cependant, les calculs montrent qu’environ 80% de la tension nominale (2,1 V) délivrée par une batterie plomb-acide proviennent uniquement des effets relativistes, principalement de PbO₂ et de PbSO₄, ce qui explique pourquoi les batteries étain-acide ne fonctionnent pas[13] - [14].

• (en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Relativistic quantum chemistry » (voir la liste des auteurs).

• (en) P. A. Christiansen, W. C. Ermler et K. S. Pitzer, « Relativistic Effects in Chemical Systems », Annual Review of Physical Chemistry, vol. 36,‎ 1985, p. 407–432 (DOI 10.1146/annurev.pc.36.100185.002203)