Pendule de Foucault

Sans tenir compte de la rotation de la Terre par rapport à un référentiel galiléen et dans le cas de petites oscillations, les équations du mouvement sont celles du pendule simple, à savoir : ${\displaystyle \left\{{\begin{matrix}{\ddot {x}}=-\omega ^{2}x\\{\ddot {y}}=-\omega ^{2}y\end{matrix}}\right.}$ où ω est la pulsation propre du pendule simple, soit : ${\displaystyle \omega ={\sqrt {g/l}}}$ où g est l'accélération de la pesanteur et l la longueur du pendule. À titre d'exemple, si à l'instant t = 0, le pendule passe en O avec la vitesse V₀ selon l'axe Ox, alors, la solution à ce système est :

${\displaystyle \left\{{\begin{matrix}x=&{V_{0} \over \omega }\sin(\omega t),\\y=&0.\end{matrix}}\right.}$

Avec la rotation de la Terre par rapport à un référentiel galiléen, il faut tenir compte des forces induites par la rotation dont tout particulièrement l'accélération de Coriolis. Cette dernière s'écrit ${\displaystyle -2\Omega ({\vec {k}}\wedge {\vec {v}})}$ où ${\displaystyle {\vec {v}}}$ est la vitesse du pendule par rapport à la Terre, ${\displaystyle {\vec {k}}}$ est le vecteur unitaire porté par l'axe de rotation terrestre et Ω la vitesse de rotation angulaire de la Terre (à savoir un tour en un jour sidéral). Cette vitesse de rotation Ω est beaucoup plus faible que la pulsation propre ω du pendule.

Si on se trouve à la latitude θ, alors le vecteur ${\displaystyle \Omega {\vec {k}}}$ se décompose, dans un repère lié au sol, en une composante de valeur ${\displaystyle \Omega \sin {\theta }}$ sur une verticale du lieu et une composante ${\displaystyle \Omega \cos {\theta }}$ dans un plan horizontal dont on peut orienter l'axe des coordonnées y vers le nord pour simplifier. Dans ce repère, le vecteur ${\displaystyle \Omega {\vec {k}}}$ a pour coordonnées ${\displaystyle {\begin{pmatrix}0\\\Omega \cos {\theta }\\\Omega \sin {\theta }\end{pmatrix}}}$. Si on note ${\displaystyle {\begin{pmatrix}{\dot {x}}\\{\dot {y}}\\{\dot {h}}\end{pmatrix}}}$ les coordonnées du vecteur ${\displaystyle {\vec {v}}}$, l'accélération de Coriolis subie par le pendule ${\displaystyle -2\Omega ({\vec {k}}\wedge {\vec {v}})}$ a pour composantes ${\displaystyle {\begin{pmatrix}2{\dot {y}}\Omega \sin {\theta }-2{\dot {h}}\Omega \cos {\theta }\\-2{\dot {x}}\Omega \sin {\theta }\\2{\dot {x}}\Omega \cos {\theta }\end{pmatrix}}}$.

En négligeant l'influence des déplacements verticaux (h), les équations du mouvement dans le plan Oxy deviennent : ${\displaystyle \left\{{\begin{matrix}{\ddot {x}}=-\omega ^{2}x+2{\dot {y}}\Omega \sin {\theta },\\{\ddot {y}}=-\omega ^{2}y-2{\dot {x}}\Omega \sin {\theta }.\end{matrix}}\right.}$

En utilisant la notation complexe ${\displaystyle z=x+iy}$, le système à résoudre se réduit à l'équation : ${\displaystyle {\ddot {z}}+2i\Omega \sin {\theta }{\dot {z}}+\omega ^{2}z=0.}$

Proposons une solution classique de la forme ${\displaystyle z(t)=e^{rt}}$, on en déduit que le complexe ${\displaystyle r}$ doit vérifier l'équation du second degré : ${\displaystyle r^{2}+2i\Omega \sin(\theta )r+\omega ^{2}=0}$ qui s'écrit aussi : ${\displaystyle \left(r+i\Omega \sin(\theta )\right)^{2}-i^{2}\omega ^{2}\left(1+\sin ^{2}(\theta ){\frac {\Omega ^{2}}{\omega ^{2}}}\right)=0.}$

En notant ${\displaystyle \omega _{0}={\sqrt {\omega ^{2}+\Omega ^{2}\sin ^{2}(\theta )}}}$, les deux solutions de l'équation du second degré sont: ${\displaystyle r=-i(\Omega \sin(\theta )\pm \omega _{0})}$ et on peut alors en déduire que la solution générale du système est de la forme:

${\displaystyle z(t)=e^{-i\Omega \sin {\theta }t}\left(c_{1}e^{i\omega _{0}t}+c_{2}e^{-i\omega _{0}t}\right).\qquad \qquad (1)}$

où ${\displaystyle c_{1}}$ et ${\displaystyle c_{2}}$ sont deux constantes indépendantes, en général complexes, qu'on peut déterminer par deux conditions initiales indépendantes comme, la position du pendule et sa vitesse à la date ${\displaystyle t=0}$ qui conduisent aux deux équations:

${\displaystyle \left\{{\begin{aligned}z(0)=&c_{1}+c_{2}\,,\\{\dot {z}}(0)=&-i\left(\Omega \sin(\theta )z(0)-\omega _{0}(c_{1}-c_{2})\right).\end{aligned}}\right.}$

En remplaçant les expressions trouvées pour les deux constantes dans l'équation (1), on peut alors écrire une équation plus aisément interprétable :

${\displaystyle z(t)=e^{-i\Omega \sin {\theta }t}\left[z_{0}\left(\cos(\omega _{0}t)+i{\frac {\Omega \sin \theta }{\omega _{0}}}\sin(\omega _{0}t)\right)+{\frac {{\dot {z}}_{0}}{\omega _{0}}}\sin(\omega _{0}t)\right].\qquad \qquad (2)}$

Ainsi, si la vitesse initiale ${\displaystyle {\dot {z}}_{0}}$ est nulle et si la position initiale est écartée du point d'équilibre, c'est-à-dire ${\displaystyle z_{0}}$ non nulle, la trajectoire au sol du pendule dans un repère tournant selon une pulsation ${\displaystyle \Omega \sin(\theta )}$ est une ellipse parcourue en une période de ${\displaystyle {\frac {2\pi }{\omega _{0}}}}$.

Si ${\displaystyle {\dot {z}}_{0}}$ est non nulle mais un imaginaire pur, le mouvement elliptique est perturbé par une oscillation perpendiculaire au plan principal d'oscillation et de même fréquence ${\displaystyle \omega _{0}\,}$.

Le pendule est libéré lorsqu'on brûle la corde. La vitesse initiale est donc nulle par rapport à la Terre, mais le pendule ne revient pas exactement dans le même plan mais légèrement décalé démontrant ainsi la rotation de la Terre par rapport aux astres célestes. Au bout d'une heure le public, nombreux en 1902 pour le cinquantenaire, pouvait voir que le plan d'oscillation s'était décalé de 11°.

Examinons alors deux manières de lancer le pendule:

• Supposons que le pendule soit propulsé depuis la position d'équilibre (${\displaystyle z(0)=0}$) vers l'est à la vitesse ${\displaystyle V_{0}}$ (${\displaystyle {\dot {z}}(0)=V_{0}}$) et nous obtenons le mouvement décrit par l'équation :

${\displaystyle z(t)={\frac {V_{0}}{\omega _{0}}}\sin(\omega _{0}t)e^{-i\Omega \sin(\theta )t}.}$

L'exponentielle complexe mise en facteur montre que la dynamique du pendule se décompose en un mouvement pendulaire simple (sinusoïdal de pulsation ${\displaystyle \omega _{0}}$) au sein d'un plan qui tourne lentement en raison de la rotation de la Terre (${\displaystyle \Omega }$) mais dont seule la composante verticale en ce lieu, ${\displaystyle \Omega \sin(\theta )}$, ne compte.

À chaque oscillation, le pendule repasse exactement par sa position de lancement qui est aussi sa position d'équilibre. On ne voit pas comment un tel mouvement peut être initié de manière simple. Dans le cas général, le pendule s'écarte de part et d'autre du plan tournant et ce n'est que par cet artefact de conditions initiales très difficiles à réaliser en pratique que le mouvement pourrait rester dans un plan et osciller au sein de ce plan comme un pendule simple.

• Supposons, comme le fit Foucault, que le pendule soit écarté de sa position d'équilibre par une corde tendue (par exemple vers l'est depuis une position distante de ${\displaystyle z_{0}}$ mètres par rapport à l'équilibre) et qu'on la brûle (voir un détail du lancement lors du cinquantenaire en 1902) afin de libérer le pendule avec une vitesse initiale nulle (${\displaystyle {\dot {z}}_{0}=0}$) [8], on obtient la solution suivante :

${\displaystyle z(t)=z_{0}e^{-i\Omega \sin(\theta )t}\left[\cos(\omega _{0}t)+i{\frac {\Omega \sin(\theta )}{\omega _{0}}}\sin(\omega _{0}t)\right]\qquad \qquad (3)}$

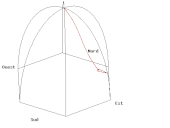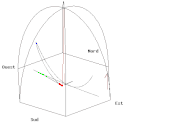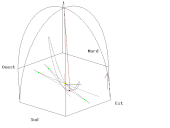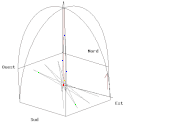
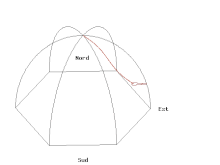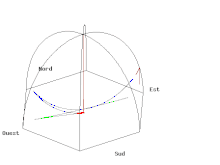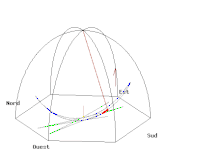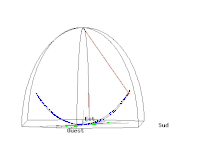
Il suffit de tracer la courbe paramétrée par la partie réelle (longitude est) et la partie imaginaire (latitude nord) pour obtenir le tracé au sol de couleur verte de l'animation A (cliquer sur l'animation pour lire le programme de tracé en langage Gnuplot correspondant) même si la vitesse de rotation de la Terre est très exagérée (pour une visualisation des phénomènes) et de l'ordre d'une rotation en 110 secondes au lieu d'une rotation par 24 heures.

Si on met une caméra dans le plan d'oscillation du pendule, on obtient l'animation B où le référentiel terrestre tourne. On peut remarquer, contrairement au cas simple examiné précédemment mais qui correspondait à un lâcher difficilement réalisable, que le pendule n'oscille pas rigoureusement dans le plan tournant mais s'en écarte de part et d'autre selon l'ellipse de couleur bleue décrite dans la grande parenthèse de l'équation (3).

B. Pendule de Foucault de 67 mètres lâché au Panthéon de Paris à une distance de 50 mètres à l'est du point d'équilibre avec une vitesse initiale nulle. La vitesse de rotation de la Terre est exagérée (1 tour en 110 secondes), comme aussi l'amplitude d'oscillation. Vue d'une caméra liée au plan d'oscillation.

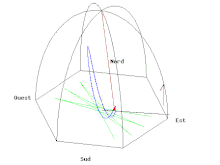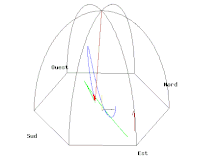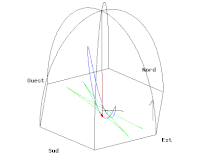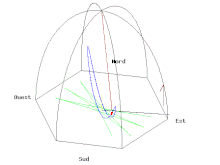
Il est également possible de voir le même pendule depuis le soleil, c’est-à-dire depuis une caméra fixe par rapport aux étoiles (animation C).

C. Pendule de Foucault de 67 mètres lâché au Panthéon de Paris à une distance de 50 mètres à l'est du point d'équilibre avec une vitesse initiale nulle. La vitesse de rotation de la Terre est exagérée (1 tour en 110 secondes). Vue d'une caméra liée au soleil.

Le pendule de Foucault du Panthéon à Paris oscille avec une pulsation propre ${\displaystyle \omega _{0}}$ extrêmement proche de celle du pendule simple ${\displaystyle \omega }$ (les 8 premiers chiffres sont identiques) puisque ${\displaystyle \Omega }$ est très petit devant ${\displaystyle \omega }$. La période d'oscillation, ${\displaystyle T={\frac {2\pi }{\omega }}=2\pi {\sqrt {\frac {l}{g}}}}$ vaut, si la longueur du fil fait 67 mètres, 16,42 secondes.

Le rapport du petit côté de l'ellipse sur le grand côté a pour expression ${\displaystyle {\frac {\Omega \sin(\theta )}{\omega _{0}}}}$ et est très petit. Le pendule de Foucault oscille donc quasiment dans un plan qui tourne en raison de la rotation de la Terre. Mais le plan n'effectue un tour complet en 24 heures qu'aux pôles. À une latitude ${\displaystyle \theta }$ donnée, la période, ${\displaystyle {\frac {2\pi }{\Omega \sin(\theta )}}}$, inversement proportionnelle au sinus de cette latitude, est plus longue. Cette période définit le jour pendulaire (pendulum day). Le sinus de 30° valant 1/2, un pendule de Foucault implanté à une latitude de 30° effectuerait un tour complet en 48 heures. La durée d'une rotation complète d'un pendule de Foucault situé à une latitude autre que l'équateur permet ainsi de déterminer cette latitude indépendamment de toute autre mesure. À la latitude nord de 48°50'46'' du Panthéon à Paris, le plan fait un tour complet en T = 31 h 47 min et 16 s ; et, en une heure, il tourne de ${\displaystyle -\Omega \sin \left({\frac {(48+52/60)\times 2\pi }{360}}\right)\times {\frac {360^{\circ }}{2\pi }}\times 3600=-11^{\circ }19'\quad }$, où ${\displaystyle \Omega \approx {\frac {2\pi }{86164}}}$ est la vitesse de rotation de la Terre sur elle-même, exprimée en radians par seconde, et correspondant à la durée du jour sidéral qui est de 23 heures, 56 minutes et 4 secondes.

D. Lâcher du pendule de Foucault à 6 mètres à l'est du centre de la coupole du Panthéon à Paris : traces au sol des 3 premières oscillations (longitudes en mètres, latitudes en millimètres)

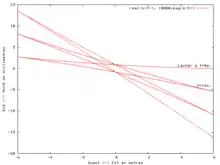
La figure D, ci-contre, représente les 3 premières oscillations après un lâcher à vitesse nulle à une distance de 6 mètres à l'est du centre de la coupole du Panthéon. Étant donné la faible déviation vers le nord par rapport au déplacement est-ouest du pendule durant ces trois premières oscillations, l'échelle de l'ordonnée (sud-nord) est multipliée par 1000 ce qui correspond à un déplacement en millimètre. La force de Coriolis, perpendiculaire au déplacement et proportionnelle à la vitesse, fait dévier le pendule de son plan d'oscillation initial vers le nord ; elle est maximale lorsque la vitesse est maximale c’est-à-dire lorsque le pendule passe près du point d'équilibre, qu'il dépasse de ${\displaystyle z_{0}{\frac {\Omega \sin(\theta )}{\omega _{0}}}=0,86\,\mathrm {mm} }$ au nord. Le pendule s'arrête au bout d'une demie période (donc 8,21 secondes) à l'opposé et a encore été dévié vers le nord. Au retour, le sens de la vitesse est inversé et la force de Coriolis fait déplacer le pendule vers le sud. Il passe à 0,86 mm au sud du point d'équilibre puis s'arrête à 5,4 mm au sud du point de lancement à la fin de la période d'oscillation soit après 16,42 secondes : avec un fil assez long respectant la latitude, il est possible de rendre (presque) visible à l’œil le déplacement sur le chemin circulaire entre une période et l'autre (vitesse tangentielle discrétisée), en transformant l'expérience en une démonstration spectaculaire. La vitesse du pendule par rapport à notre repère terrestre étant alors nulle, la force de Coriolis est donc nulle et le pendule repart dans la même direction en effectuant un point de rebroussement.

On remarque sur les figures A, B et C un poteau central éclairé par le soleil (le lâcher est simulé à midi un jour d'équinoxe) et son ombre portée sur le sol. Si l'extrémité du pendule se terminait par une tige de 0,86 mm de diamètre, le diamètre de ce poteau ne devrait pas excéder lui aussi 0,86 mm pour que ce dernier ne soit pas emporté à la première oscillation. Il semble néanmoins assez irréaliste d'installer un tel poteau, comme une fibre optique, car les fluctuations dues aux imperfections du lancer, aux courants d'air, aux vibrations de toute sorte, etc., semblent beaucoup plus importantes.

• Umberto Eco, Le Pendule de Foucault, roman
• Camille Flammarion, « Notice scientifique sur le pendule du Panthéon, expérience reprise en 1902 au nom de la Société astronomique de France », Société astronomique de France, Paris, 1902 (lire en ligne)
• Jacques Gapaillard, Et pourtant, elle tourne! le mouvement de la Terre, Paris, Éd. du Seuil, coll. « Science ouverte », 1993, 347 p. (ISBN 978-2-02-013157-5, OCLC 708325384)
• Attilio Rigamonti, Andrey Varlamov (en) et Jacques Villain, Le kaléidoscope de la physique, Belin / Pour la science, coll. « Bibliothèque scientifique », 2014 (ISBN 978-2-7011-6487-8, OCLC 896818621), « 4. Le pendule de Foucault et la force de Coriolis », p. 34-43

• Foucault, Démonstration physique du mouvement de rotation de la Terre au moyen du pendule, Comptes Rendus des Séances de l'Académie des Sciences (1851), Paris, 32, 135-138.
• Binet J., Note sur le mouvement du pendule simple en ayant égard à l'influence de la rotation diurne de la Terre, Comptes Rendus des Séances de l'Académie des Sciences (1851), Paris, 32, 157-159, 160, 197-205.
• Poinsot L., Remarques sur l'ingénieuse expérience imaginée par M. Léon Foucault pour rendre sensible le mouvement de rotation de la Terre, Comptes Rendus des Séances de l'Académie des Sciences (1851), Paris, 32, 206-207.
• Antinori, Anciennes observations faites par les membres de l'académie del Cimento sur la marche du pendule, Comptes Rendus des Séances de l'Académie des Sciences (1851), Paris, 32, 635-636.
• Poncelet, Nouvel examen de la question relative aux oscillations tournantes du pendule à libre suspension, et ayant égard à l'influence de la rotation de la Terre, Comptes Rendus des Séances de l'Académie des Sciences (1860), Paris, 51, 467-476, 511-524.
• Serret J.-A., Le pendule de Léon Foucault, Comptes Rendus des Séances de l'Académie des Sciences (1872), Paris, 74, 269-276.
• Gilbert Ph., Les preuves mécaniques de la rotation de la Terre, Bulletin des Sciences Mathématiques, rédigé par M. Darboux. Paris. 6, (1882), 205-223.
• «Le pendule de Foucault ; Mémoire de 1851 et autres textes» ; Éditions Nielrow ; Dijon 2019 ; (ISBN 978-2490446117)

• Jean Bernard Léon Foucault
• Pendule pesant
• Lois du mouvement de Newton

• En vidéo : reconstitution de l'expérience du pendule de Foucault à la cathédrale de Genève, avec de nombreuses explications;
• Petite histoire du pendule de Foucault sur le site Sciences physiques et chimiques de l'Académie de Nantes, avec notamment une photo où l'on voit Camille Flammarion et Alphonse Berget regarder le mouvement du pendule après que Joseph Chaumié, ministre de l'instruction publique, ait brûlé la corde retenant le pendule lorsque l'expérience avait été renouvelée au Panthéon le 22 octobre 1902 pour le cinquantenaire.
• Démonstration animée (Flash);
• Jolies illustrations et intéressants commentaires scientifiques sur le pendule de Foucault.