Vitesse relative

Si la vitesse exprime de façon générale la variation d'une quantité (autre que le temps, comme la température, la pression, le poids etc.) par rapport à une durée (écart de temps), ce qui suit ne concerne que les domaines de la cinématique et de la mécanique : mécanique newtonienne ou mécanique relativiste. Par vitesse on entendra donc distance[1] parcourue par unité de temps. La vitesse relative étant une vitesse, elle pourra être définie, suivant les besoins, par une seule grandeur scalaire (20 km/h, 1 tour par minute) ou par plusieurs grandeurs permettant d'en préciser les caractéristiques, comme la direction et le sens. (Voir dans l'article sur la vitesse : vecteur vitesse, vitesse angulaire, vitesse aréolaire, vitesse instantanée, vitesse moyenne, vitesse curviligne.)

Les exemples qui suivent n'ont pas pour objectif d'expliciter les théories de la physique relativiste (relativité restreinte, relativité générale). Cependant l'intérêt qu'elles présentent sera abordé, quand la mécanique classique atteint ses limites de validité (en cohérence ou en précision).

Il pourra s'avérer utile de consulter les articles consacrés à certains termes scientifiques comme référentiel galiléen ou spécifiques à un métier, en particulier pour les exemples concernant la navigation maritime.

Schéma 1 - Croisement d'automobiles

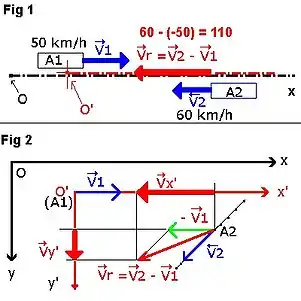
Deux automobiles circulent sur une route à deux voies à des vitesses constantes de 50 km/h et de 60 km/h. Elles roulent dans leur couloir de circulation dans des sens opposés et vont donc se croiser. Que la route soit rectiligne ou sinueuse, qu'elle monte et qu'elle descende, et bien que la terre soit ronde, la figure 1 du schéma 1 est une représentation de leur situation dans un repère cartésien dont l'axe principal Ox correspond à la ligne (blanche ou jaune) séparant les deux voies de circulation, l'autre axe, perpendiculaire, permettant de les représenter dans un plan (plan du schéma).
On peut ainsi définir trois référentiels :

• un référentiel route, Rr, dont l'axe principal est Ox, où la route suivie est développée en ligne droite,
• un référentiel auto A1, RA1, dont l'axe principal est O'X, O' correspondant à la position de A1 sur Ox, s'éloignant de O à la vitesse V1
• un référentiel (non représenté sur le schéma) RA2 pour l'auto A2 avec un axe d'origine O" dirigé vers O.

Ces définitions de repères étant faites, les deux automobiles étant assimilées aux points mobiles O' et O", on peut calculer les vitesses relatives suivantes :

• Le vecteur vitesse relative de A2 par rapport à A1, soit la vitesse de A2 dans RA1, est ${\displaystyle {\vec {Vr}}={\vec {V_{2}}}-{\vec {V_{1}}}}$
• Le vecteur vitesse relative de A1 par rapport à A2 est ${\displaystyle {\vec {Vr'}}={\vec {V_{1}}}-{\vec {V_{2}}}=-{\vec {Vr}}}$
• A1 et A2 s'approchent l'une de l'autre à une vitesse de ${\displaystyle \left|V_{1}-(-V_{2})\right|=\left|V_{2}-(-V_{1})\right|}$ , soit 50-(-60) = 60-(-50) = 110 km/h.

Les vitesses relatives sont ici, tels que les référentiels ont été définis, le résultat de la différence des vitesses que l'on qualifiera d'« absolues ». En effet, sur l'axe Ox, O étant un observateur des mouvements de O' (automobile A1) et de O" (automobile A2), la vitesse relative des deux mobiles est bien aussi la variation dans le temps de la distance curviligne (sur le bitume de la route) qui les sépare . Cependant, c'est une approximation, les deux mobiles ne suivant pas strictement le même parcours, celui-ci ayant déjà été assimilé à celui de la ligne blanche.
Supposons que nous prenions un autre référentiel, basé sur la carte routière où les deux autos circulent. Nous pourrions nous retrouver, suivant la sinuosité du parcours, à un instant t, dans la situation de la figure 2 du schéma 1. Les vitesses relatives pourraient, à l'instant t, faire l'objet des mêmes opérations de soustraction (ou d'addition) de vecteurs. Mais elles n'auraient aucune utilité, les vitesses des deux mobiles dans ce référentiel variant dans le temps en norme et direction. Sans aller jusqu'à un référentiel sphérique montagneux, où l'on tenterait de faire la différence de leurs vitesses absolues pour obtenir leurs vitesses relatives !
Par contre, si la figure 2 du schéma 1 représente deux mobiles en mouvement de translation rectiligne uniforme dans le repère Ox-Oy, alors ${\displaystyle {\vec {Vr}}}$ représente bien la vitesse relative de A2 par rapport à A1, ${\displaystyle {\vec {Vx'}}}$ et ${\displaystyle {\vec {Vy'}}}$ ses composantes dans le repère lié à A1 (dont un des axes, O'x', représente sa propre route).
Autrement dit, les additions ou soustractions de vecteurs vitesses entre repères n'ont de sens que dans des référentiels galiléens.

Schéma 2 - Vitesses et vents relatifs sur un navire

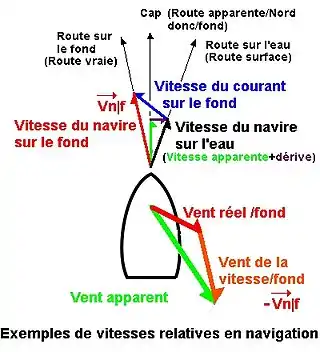
En navigation, qu'elle soit aérienne ou maritime, les routes sont des chemins théoriques, ne mettant à la disposition du navigateur ni des lignes blanches ni des délinéateurs. Le schéma 2 représente un voilier naviguant sur une mer se déplaçant sur le fond (la terre) suivant un courant marin ou un courant de marée. Il suit un cap (cap compas), par rapport au Nord, un des axes d'un repère terrestre. L'axe du navire est orienté suivant cette direction, et la navire suit une route apparente suivant ce cap.
Nous sommes en présence d'un seul mobile suivant des routes différant selon le référentiel : référentiel terrestre (le fond), référentiel surface (la mer). Les mesures que le navigateur (l'observateur) peut effectuer, se rapportent, sont relatives à son propre référentiel [2]:

• vitesse apparente sur l'eau suivant son cap, indiquée par son loch,
• vitesse apparente du vent en intensité et orientation (vent apparent), indiquée par son anémomètre et sa girouette,

D'autres données lui sont fournies dans un référentiel terrestre :

• vecteurs courant d'heure en heure[3].

Si le navigateur veut connaître le vent réel (vent dans un repère terrestre) il lui faudra estimer sa vitesse sur le fond, donc la vitesse d'entraînement de son référentiel dans le référentiel terrestre. Il fera de simples additions ou soustractions de vecteurs pour déterminer sa route vraie.
S'il veut corriger (infléchir) sa route en fonction de modifications prévisibles des vitesses du courant ou du vent (météo), il fera des prévisions heure par heure (les courants étant indiqués heure par heure), en considérant qu'entre deux positions espacées d'une heure, tous les mouvements relatifs sont uniformes (vecteurs vitesse).
Il est à remarquer que le référentiel du mobile est ici basé sur un repère

• en mouvement linéaire et uniforme (dans un bref intervalle de temps) par rapport au référentiel terrestre matérialisé par une carte marine,
• axé sur sa route apparente.

Schéma 3 - Route de collision et vitesses relatives

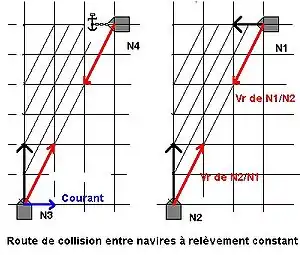
Deux navires N1 et N2 suivent des routes en surface telles que figurées sur le schéma 3. N1 fait route à l'Ouest à 5 nœuds (Mille marin par heure), N2 à 10 nœuds vers le Nord (sur le schéma 3, comme sur les cartes, le Nord est en haut).

Quel que soit le vecteur courant, supposé le même sur toute la zone, un observateur sur N2, observant que le relèvement) de N1 est constant [4] et constatant visuellement que le bateau s'approche (par sa taille apparente) en déduit logiquement qu'il va entrer en collision avec N1 (même constatation depuis N1 vis-à-vis de N2). Dans le référentiel de N2, (N2 étant l'origine d'un repère dont un axe est sa route, l'autre étant perpendiculaire) la vitesse relative, ou apparente, de N1 est orientée vers l'origine de N2.

Leur vecteur vitesse relative est égal à la différence vectorielle de leurs vecteurs vitesses en surface (ou de leurs vecteurs vitesses fond).

Un navire N4 est à l'ancre; sa vitesse fond est nulle mais sa vitesse surface est égale et opposée au courant de 5 nœuds, venant de l'Ouest. N3 fait route au Nord à 10 nœuds. N3 constate qu'il est en route de collision avec N4 car il perçoit une vitesse relative de N4 orientée vers lui dans son référentiel.
N3 fait donc les mêmes observations que N2. Si N3 ne connaît pas l'existence du courant et ne sait pas que N4 est au mouillage (ancré sur le fond); il aura la même perception de route apparente, de vitesse relative, dans son référentiel, que N2 dans le sien.
La route de collision est une route sur le fond entre N3 et N4, c'est la route "vraie", suivie par N3 car N4 est fixe dans un repère lié au fond.
La route de collision N1 et N2 est une route observée dans les référentiels liés à chaque navire. Elle n'est que théorique dans un repère déterminé par un observateur fixe sur la surface de la mer, c’est-à-dire un observateur situé sur un navire à l'arrêt sur l'eau, dérivant comme le courant. Tout observateur fixe par rapport à la mer, (comme N1 et N2 s'ils prennent pour origine de leur référentiel leur position à un instant donné), verra N1 et N2 suivre deux routes concourantes en un point où ils seront présents au même instant.
Dans l'exemple du schéma 3, N1 et N2 suivent des routes, sur la surface de la mer, perpendiculaires (Sud-Nord et Est-Ouest) se croisant au moment de la collision.

N1 et N2 suivent, soit des routes les menant à la collision (référentiel surface), soit une route de collision (référentiels liés aux mobiles).
En fonction du mouvement relatif (vitesse d'entraînement dû au courant) du référentiel surface par rapport à un référentiel terrestre (le fond), les deux navires suivront également deux routes différentes (selon leurs vitesses par rapport au fond) les menant, au même instant, quel que soit le courant, à une collision.

Les référentiels liés aux mobiles sont déterminés à partir d'un référentiel qui leur est commun. Pour apprécier le fait qu'ils sont en route de collision les deux mobiles vont se repérer par rapport à :

• un angle (gisement) par rapport à leur vecteur vitesse surface (sur l'eau) , et ils supposent qu'ils suivent un cap constant sur l'eau et que la surface de la mer est un repère fiable (non absolu, mais presque, les courants qu'ils subissent étant identiques),
• ou bien un angle par rapport au Nord (relèvement), donc par rapport au fond, qu'ils considèrent aussi comme un référentiel fixe (absolu), ou l'axe donné par un gyroscope. Ce qui revient au même axe si les courants sont fixes pendant l'observation.

Ce qui est équivalent à dire que l'observateur d'un navire considère (que le temps est uniforme, la question ne se posant pas réellement) que l'espace qu'il définit (entre son navire et le navire qui approche) est figé en dimensions (les distances entre deux points quelconques de cet espace ne varient pas en fonction du temps). Dans les deux cas il considère que le courant de surface, s'il existe, suit une direction constante par rapport au fond, que les diverses dérives sont constantes. L'observateur, dans les exemples précédents, établit donc un référentiel où lui-même représente l'origine (ou bien sa position à un instant donné) et un axe orienté par rapport à un autre référentiel, en l'occurrence son vecteur vitesse dans un autre référentiel. Si l'observateur n'a aucun moyen de connaître son vecteur vitesse dans un référentiel où il évolue (pas de compas, aucune mesure de vitesse, donc aucun repère extérieur), la présence d'un objet lui permettra de déterminer un axe entre lui et l'objet. S'il peut mesurer (estimer) une distance, la variation dans le temps (son axe des temps) de cette distance lui permettra de calculer leur vitesse relative. À grande distance ils sont a priori sur une route de collision. Ce n'est que lorsque l'autre objet prend une dimension mesurable qu'il peut lever le doute. (Voir parallaxe)

La notion de vitesse relative devient plus complexe dès que les mobiles ne se déplacent plus dans des repères galiléens (mouvements rectilignes à vitesse constante). Tout en restant dans les domaines où il n'est pas nécessaire de faire intervenir les théories de la relativité, quelques exemples permettent de juger, en mécanique classique, de l'importance de la définition des référentiels.

Schéma 4 - Dans un référentiel galiléen (le plan du schéma) M1 suit une trajectoire rectiligne accélérée, M2 suit une trajectoire inclinée à 30° à vitesse constante. La courbe en vert représente la trajectoire de M2 vue dans le référentiel de M1 (OxOy), Ox étant sa route. La courbe en bleu représente la trajectoire de M1 vue par M2, dans son référentiel (OxOy), Ox étant également déterminé par sa propre route. La symétrie est facile à constater ainsi que la courbure apparente (relative) des trajectoires. (Construction géométrique)

Un exemple simple est celui du passager d'une automobile en accélération ou au freinage. Dans ce cas les deux mobiles sont la voiture et le passager, le repères sont la route (en ligne droite), le repère lié à la voiture et le repère lié au passager. La colinéarité des mouvements, ou du moins la colinéarité implicite des trajectoires (parallèles et proches, donc confondues), puisque dans un espace réduit elles permettent aisément d'admettre que localement la route constitue un référentiel galiléen et que l'axe principal est commun, permettent de continuer à admettre que leurs vitesses instantanées relatives sont la différence de leurs vitesses absolues;

Si l'on nomme vitesse d'entraînement la vitesse qu'un mobile (le conducteur) aurait dans le référentiel accéléré (l'automobile), qui est dans ce cas la vitesse absolue de l'automobile (dans un repère non accéléré, ou galiléen), on peut toujours écrire que les vecteurs vitesses dans le référentiel accéléré sont tels que :

${\displaystyle {\vec {v}}_{relative}={\vec {v}}_{absolue}-{\vec {v}}_{entrainement}}$,

ainsi que pour leurs accélérations :

${\displaystyle {\vec {a}}_{relative}={\vec {a}}_{absolue}-{\vec {a}}_{entrainement}}$

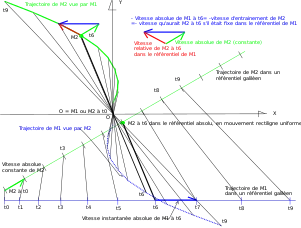
Si l'on considère maintenant deux mobiles repérés dans un référentiel "absolu" ou galiléen, suivant des trajectoires non colinéaires, dont l'un (M1) est animé d'une vitesse variable, accélérée, comme sur le schéma 4, on peut constater que :

• le mobile M2 (à vitesse constante dans le référentiel « absolu ») ne suit pas une trajectoire rectiligne dans le référentiel non inertiel de M1. Sa vitesse relative varie (son vecteur vitesse varie en norme et en direction); il est donc doté, pour M1, d'une accélération relative apparente alors qu'en « absolu » il n'en a pas;
• le mobile M1, vu par M2, semble également suivre une trajectoire courbe;
• les deux trajectoires sont symétriques par rapport à l'origine des repères relatifs;

Les tracés pourraient correspondre aux routes droites et divergentes suivies par deux automobiles dont l'une accélère (M1) et l'autre maintient une vitesse constante (M2). Les repères relatifs, confondus ici sur le schéma 4, seraient alors :

• Ox : la route suivie, en direction en sens, par chacun des véhicules,
• Oy : 90° à gauche de la route suivie.

Si les vitesses relatives instantanées sont encore égales à la différence des vitesses absolues instantanées, ce n'est visiblement plus le cas pour les accélérations, puisque les trajectoires relatives sont curvilignes, donc que les vitesses relatives changent de direction.

Schéma 5 - Le mobile M traverse un disque tournant dans le sens anti-horaire dans un référentiel où sa trajectoire est un segment de droite AB qu'il parcourt à vitesse constante. Vu depuis un référentiel lié au disque, il effectue les trajectoires curvilignes AOC, AOA et AOB si, pendant la durée de sa traversée, le disque fait respectivement 1/4, 1/2 et 1 tour.

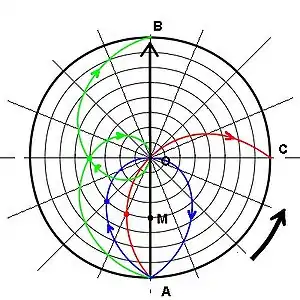
Le schéma 5 visualise les parcours d'un même mobile M, en trajectoire linéaire uniforme (à vitesse constante) dans un repère d'observation, et ses trajectoires vues dans un repère lié au disque en rotation uniforme. (Pour les formules mathématiques, voir les articles consacrés à la force de Coriolis et à l'accélération de Coriolis.)
Sur ce schéma 5, seules sont représentées les trajectoires. Les vitesses peuvent s'imaginer, elles sont à chaque instant tangentes aux trajectoires.
Certains vecteurs vitesses sont détaillés sur le schéma 6. Le schéma 5 décrit :

• un disque centré en O, tournant à vitesse de rotation constante (sens de la flèche, soit trigonométrique ou anti-horaire) autour de O,
• un mobile M traversant le disque à vitesse uniforme.

Ce mobile est par exemple un objet glissant sans frottement [5] sur le disque (comme une savonnette humide), ou un objet roulant au-dessus du disque dans une gouttière. M est donc un point animé (dans un référentiel galiléen) d'une vitesse rectiligne constante. Son mouvement est indépendant du mouvement du mouvement de rotation du disque. Les courbes décrivent les trajectoires relatives du point M, vues par tout point fixe sur le disque :

• AOC (en rouge) est la trajectoire apparente du point M quand le disque fait 1/4 de tour pendant que M en parcourt exactement un diamètre;
• AOA (en bleu) si le disque fait 1/2 tour pendant que M le traverse;
• AOB (en vert) si le disque fait 1 tour.

Ce schéma permet de visualiser la construction géométriques des trajectoires relatives, où les points sont relevés en 1/16 ^e de tour et en 1/16 ^e de diamètre. Pour étudier de plus près les vitesses relatives le schéma 6 détaille le cas où le disque fait 1/2 tour pendant que M parcourt un diamètre.

Schéma 6 - Trajectoires relatives de deux mobiles. M est en translation, A en rotation dans un référentiel « absolu ». Les trajectoires bleues et rouges représentent les mouvements de M et de A, vus respectivement par A et M, dans leurs référentiels propres (devant, à gauche, à droite).

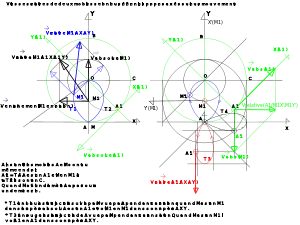
Dans un référentiel absolu galiléen, R, celui du dessin, quand A est en A1, M est en M1 et le référentiel R' de A1 est A1X', A1Y'. Projeté dans R, le vecteur vitesse relative de M1, en noir, est la différence vectorielle de la vitesse absolue de M1 (en translation uniforme dans R) et de sa vitesse d'entraînement, c'est-à-dire la vitesse qu'aurait M1 s'il était fixe dans R'. Autrement dit, A1 voit s'éloigner M1 avec une vitesse composée d'un mouvement de translation (réel dans l'absolu) et d'un mouvement de rotation (apparent puisque M1 ne tourne pas dans l'absolu). Si A s'est fixé un référentiel de projection, où il relève les positions successives de M (ici AX,AY) , il repèrera à cet instant que M est en M'1, et doté d'une vitesse relative Vrelative(M'1/AX,AY), en bleu.

• La vitesse relative de M, vue par A, n'est pas égale à la différence de leurs vitesses absolues car le référentiel de A n'est pas galiléen.

Il en va différemment pour la vitesse relative de A, vue par M, dont la trajectoire dans R' est tracée en rouge sur sa projection dans son repère relatif AX,AY.

• Comme M se déplace à vitesse constante dans R, et donc que son repère relatif R' est galiléen, la vitesse relative des autres mobiles est égale à la différence des vitesses absolues (vecteurs en vert) :

${\displaystyle {\vec {v}}_{relativedeA/R'deM}={\vec {v}}_{absoluedeA}-{\vec {v}}_{absoluedeM}}$

Comme l'accélération d'entraînement est nulle, et que le repère relatif R' lié à M n'est pas en rotation (accélération de Coriolis nulle) :

${\displaystyle {\vec {a}}_{relativedeA/R'deM}={\vec {a}}_{absoluedeA}}$

• On peut également remarquer que les trajectoires relatives ne sont pas symétriques, ce qui laisse supposer que la variation dans le temps des vitesses relatives, donc les accélérations relatives, ne sont pas non plus similaires selon que l'on observe un mobile depuis un référentiel galiléen ou un référentiel non inertiel. Le mobile M, vu d'un référentiel lié à A, en translation et surtout en rotation par rapport au référentiel absolu, possède une accélération relative composée d'une accélération d'entraînement (due au mouvement d'entraînement en rotation du référentiel relatif par rapport au référentiel absolu) et d'une accélération complémentaire, ou accélération de Coriolis.

${\displaystyle {\vec {v}}_{relativedeM/R'deA}={\vec {v}}_{absoluedeM}-{\vec {v}}_{entrainementdeM}}$

La déformation apparente de la trajectoire de M, qui est linéaire dans le référentiel absolu, provient donc du fait que sa vitesse d'entraînement n'est pas constante. Ce qui dote donc sa vitesse relative d'une accélération non colinéaire :

${\displaystyle {\vec {a}}_{relativedeM/R'deA}=-{\vec {a}}_{entrainementdeM}-{\vec {a}}_{Coriolis}}$
(Ici, M se déplaçant à vitesse absolue constante, l'accélération absolue est nulle.)

Dans le cas général, la loi de composition des mouvements donne, pour les vitesses et accélérations relatives d'un mobile observé depuis un référentiel non galiléen :

${\displaystyle {\vec {v}}_{relative}={\vec {v}}_{absolue}-{\vec {v}}_{entrainement}}$

${\displaystyle {\vec {a}}_{relative}={\vec {a}}_{absolue}-{\vec {a}}_{entrainement}-{\vec {a}}_{Coriolis}}$

Cette loi de composition des mouvements est issue de formules de changements de repère.

Les observations les plus connues, permettant de la vérifier, sont :

• le pendule de Foucault,
• les phénomènes météorologiques qui concernent la rotation des vents,
• la déviation vers l'Est de la chute d'un corps.

À partir des exemples ci-dessus, on peut considérer que la seule définition de la vitesse relative qui reste indiscutable, si l'on admet un temps universel, est donc :

• la vitesse relative d'un mobile M1 par rapport à un mobile M2 est la variation dans le temps du vecteur position de M1 dans le référentiel de M2.

C'est à partir de cette définition qu'ont été élaborées les lois de composition des mouvements permettant de calculer les vecteurs vitesses, dérivées du vecteur position par rapport au temps et les accélérations, dérivées du vecteur vitesse par rapport au temps.

Schéma 7 - Vitesses relatives et vitesses d'entraînement lors d'un changement de référentiel. Un mobile P et un repère relatif AXY suivent des trajectoires quelconques (mais coplanaires) dans un repère Oxy.
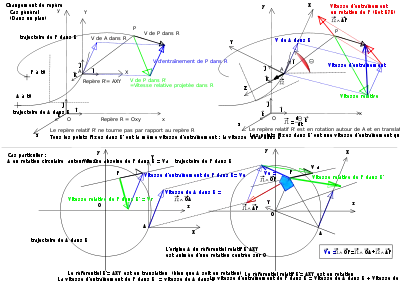
* En haut : cas général (mouvements coplanaires). * En bas : l'origine du repère relatif est en rotation par rapport à O. * À gauche : le repère relatif est en translation. * À droite : le repère relatif est en rotation.

On peut constater sur le schéma 7, que les vitesses relatives dépendent, non seulement du mouvement de l'origine du repère relatif (A sur le schéma 7), mais de l'orientation de ce repère relatif par rapport au repère de référence.

• Les vitesses relatives entre deux mobiles sont liées à la notion d'orientation.
• L'orientation du référentiel relatif peut induire une rotation.

La notion de vitesse d'entraînement est rendue compliquée du fait même de la rotation : ce n'est pas la rotation du point origine du référentiel relatif qui a de l'importance, mais la rotation du référentiel relatif par rapport au repère de référence.

Il se trouve que tout naturellement, du fait du ressenti physique (accélération de la pesanteur, forces centrifuges), nous avons tendance à prendre pour référentiel un repère basé sur notre mouvement et sur ce qui l'influence directement, déterminant ainsi des axes locaux :

• la verticale locale (attraction terrestre),
• les pôles magnétiques terrestres (Nord, Sud).

Ce qui nous complique l'expression mathématique des phénomènes quotidiens.

Les formules mathématiques de changement de référentiel sont cependant simples :

Pour le point P, toutes les dérivations (et les représentations des vecteurs) étant faites dans R :

• sa position dans la repère R étant représentée par le vecteur ${\displaystyle {\vec {OP}}}$,
• sa position dans le repère R' étant représentée par le vecteur ${\displaystyle {\vec {AP}}}$,
• la vitesse du point P dans R d'origine O est : ${\displaystyle {\frac {d{\vec {OP}}}{dt}}}$, dérivée du vecteur position par rapport au temps,
• la vitesse du point P dans R' d'origine A est : ${\displaystyle {\frac {d{\vec {AP}}}{dt}}}$,
• la rotation de R' par rapport à R étant représentée par le vecteur ${\displaystyle {\vec {\Omega }}}$ :

${\displaystyle {\frac {d{\vec {OP}}}{dt}}={\frac {d{\vec {AP}}}{dt}}+({\frac {d{\vec {OA}}}{dt}}+{\vec {\Omega }}\wedge {\vec {AP}})}$, soit : ${\displaystyle {\vec {v}}_{\textrm {absolue}}={\vec {v}}_{\textrm {relative}}+{\vec {v}}_{\textrm {entrainement}}}$

Il faut remarquer que cette opération mathématique n'implique aucune spécificité pour le repère R que l'on peut qualifier d'absolu par rapport à R', repère relatif. Il n'est pas forcément immobile.

Cette formule de changement de référentiel, dite aussi de composition des mouvements permettant de comparer les vitesses et les accélérations est cependant dépendante d'une condition importante, celle d'un chronomètre universel, valable dans les différents référentiels.

• Composition des mouvements
• Pendule de Foucault
• Déviation vers l'Est