Facteur de diffusion atomique
En physique, le facteur de diffusion atomique est une mesure de la puissance de diffusion d'une onde par un atome. Il dépend de la nature des interactions entre l'onde et l'objet diffusant, donc de la radiation incidente : en général, il s'agit de la diffusion élastique de rayons X, de neutrons ou d'électrons. En cristallographie, les facteurs de diffusion atomiques sont utilisés pour calculer le facteur de structure d'une réflexion donnée lors de la diffraction par un cristal.
Définition générale
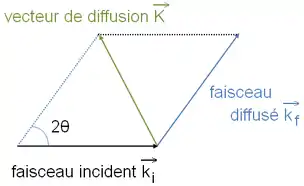
Le facteur de diffusion atomique apparaît lorsque l'on considère l'effet d'un objet (atome ou ion) sur une onde incidente , de vecteur d'onde et de longueur d'onde λ comparable à la taille de l'objet, dans l'hypothèse de la diffusion élastique. L'onde diffusée au point par l'objet situé au point origine s'écrit :
où est le vecteur d'onde de l'onde diffusée, de même longueur d'onde λ mais de direction différente. Les normes des deux vecteurs d'onde sont donc égales :
L'angle entre les vecteurs d'onde incident et diffusé est l'angle de diffusion 2θ et est le vecteur de diffusion[note 1], différence des vecteurs d'onde des faisceaux incident et diffusé et :
Le facteur de diffusion atomique est la transformée de Fourier de la distribution de densité spatiale de l'objet diffusant, de l'espace réel vers l'espace réciproque. Il est défini par :
Du fait des propriétés de la transformée de Fourier, la largeur de la fonction dans l'espace réciproque est une fonction inverse de celle de la distribution de densité dans l'espace réel : des objets larges conduisent à une décroissance rapide du facteur de diffusion.
Cas des rayons X
Les rayons X sont diffusés par le nuage électronique de l'atome et l'amplitude de la diffusion des rayons X augmente avec le numéro atomique . En conséquence, les rayons X ne permettent pas bien la détection des éléments légers tels que l'hydrogène et il y a très peu de contraste entre des éléments voisins dans le tableau périodique.
Pour la diffusion des rayons X, représente la densité électronique autour du noyau de l'atome. Le facteur de diffusion atomique est alors la transformée de Fourier de cette quantité. Il s'exprime en électrons (e−). L'approximation d'une distribution sphérique des électrons est habituellement suffisante en diffraction des rayons X[1].
Les premiers calculs du facteur de diffusion atomique furent effectués sous l'hypothèse de la diffusion Thomson et pour un atome de symétrie sphérique contenant électrons indépendants[2] - [3] - [4] - [5] - [6] - [7]. Ce facteur de diffusion atomique approché s'écrit alors comme la somme des facteurs de diffusion de chaque électron :
où est la densité électronique de l'électron et est la fonction de Bessel sphérique d'ordre 0. En négligeant les interactions entre les électrons, le facteur de diffusion atomique est donc une grandeur réelle. En particulier, dans le cas d'un vecteur de diffusion nul, le facteur de diffusion atomique est égal au numéro atomique de l'atome : . Cette formule est bien adaptée pour les éléments à faible numéro atomique et pour la diffusion de rayons X à courtes longueurs d'onde.
Interpolations
Les valeurs des facteurs de diffusion atomiques pour chaque atome et ion sont tabulées en fonction de dans les tables internationales de cristallographie[8]. En pratique, il est plus simple d'utiliser des fonctions d'interpolation numérique pour décrire les facteurs de diffusion atomiques. La fonction d'interpolation la plus souvent utilisée est valable pour compris entre 0 et 2 Å-1, cas qui correspond à la résolution de la plupart des expériences de diffraction :
Les valeurs de , , , , , , , et sont également données dans les tables internationales de cristallographie.
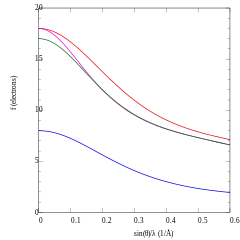
Pour compris entre 2 et 6 Å-1, le facteur de diffusion atomique est mieux interpolé par la formule logarithmique suivante[9] :
Diffusion anomale
En général, le facteur de diffusion atomique pour les rayons X est une grandeur complexe. La partie imaginaire du facteur de diffusion atomique ne devient importante que lorsque la longueur d'onde des rayons X incidents est proche d'une arête d'absorption de l'atome. On parle dans ce cas de diffusion anomale. Pour en tenir compte, deux termes correctifs sont ajoutés au facteur de diffusion atomique :
où et décrivent les variations en amplitude et en phase du facteur de diffusion par rapport à , dues à l'absorption des rayons X.
Atomes non isolés
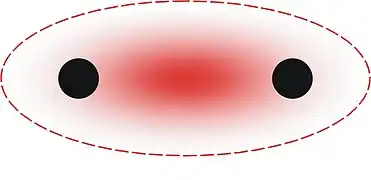
Dans un cristal, les atomes forment des liaisons chimiques entre eux. Ces liaisons déforment le nuage électronique des atomes et la symétrie de l'objet diffusant n'est plus strictement sphérique. L'effet de la déformation du nuage électronique sur le facteur de diffusion atomique est généralement faible, mais il doit être pris en compte lors de l'étude de la densité électronique dans un cristal.
La densité électronique d'un atome non isolé est calculée à partir de celle de l'atome isolé en ajoutant des termes perturbatifs. Le facteur de diffusion de l'atome non isolé est alors la transformée de Fourier de cette densité électronique perturbée.
On distingue trois types de contributions à la densité électronique, provenant d'électrons différents :
- les électrons de cœur, ne participant pas aux liaisons chimiques, ont une densité sphérique identique à celle dans l'atome isolé ;
- les liaisons chimiques ont deux effets sur la densité des électrons de valence :
- le changement de potentiel change la force de l'interaction des électrons de valence avec le noyau atomique, modifiant le rayon de leur distribution spatiale ;
- la forme de la distribution électronique n'est plus sphérique.
La densité électronique totale d'un atome est la somme de ces trois contributions :
les exposants et indiquant les contributions sphériques et asphériques des électrons de valence, respectivement.
La contribution sphérique des électrons de valence s'écrit simplement comme la contraction ou l'expansion d'un facteur de la densité électronique de valence dans l'atome isolé :
où est la population d'électrons de valence contribuant à la partie sphérique de la densité électronique.
Pour la contribution asphérique des électrons de valence, la densité électronique, exprimée dans un système de coordonnées polaires, peut généralement être décomposée en une partie radiale et une partie angulaire :
La fonction angulaire est développée sur la base des harmoniques sphériques , définies avec les polynômes de Legendre associés et avec par :
Comme la densité électronique d'un atome est une grandeur réelle, l'utilisation des harmoniques sphériques réelles normalisées (notées ), combinaisons linéaires des harmoniques sphériques, est préférée[10]. Les électrons dont la distribution n'est pas sphérique donnent donc lieu à un terme correctif pour la densité électronique de l'atome :
où est la population d'électrons contribuant au terme de la somme.
Finalement, la densité électronique d'un atome non isolé s'écrit[11] :
Dans un cristal, la densité électronique d'un atome est soumise aux contraintes de symétrie imposées par le groupe ponctuel de la position de Wyckoff sur laquelle il se trouve. Ces contraintes indiquent quels termes peuvent être présents dans l'expression de la densité électronique. Les paramètres , , et peuvent être obtenus par affinement de structure si les données ont été collectées avec une très haute résolution.
Cas des neutrons
Il existe deux différentes interactions des neutrons avec la matière : avec le noyau des atomes et avec leurs moments magnétiques.
Interactions nucléaires
La diffusion nucléaire d'un neutron libre par un noyau atomique s'effectue par le biais de l'interaction forte. La longueur d'onde des neutrons thermiques (quelques Å) et froids (jusqu'à quelques dizaines d'Å) généralement utilisée est de 4 à 5 ordres de grandeur supérieure à la taille du noyau (quelques fm). Les neutrons libres du faisceau incident se comportent comme une onde plane. Pour ceux qui sont soumis à une diffusion nucléaire, le noyau atomique agit comme une source ponctuelle secondaire et diffuse les neutrons sous forme d'onde sphérique (bien qu'il s'agisse d'un phénomène quantique, ceci peut être visualisé en termes classiques par le principe de Huygens-Fresnel). Dans ce cas représente la distribution de densité spatiale du noyau, qui est un point infinitésimalement petit comparé à la longueur d'onde des neutrons (distribution de Dirac, ). La distribution de Dirac est contenue dans le pseudo-potentiel de Fermi qui décrit la diffusion d'un neutron par un noyau :
où est la constante de Planck, la masse du neutron et la longueur (ou amplitude) de diffusion[note 2]. La transformée de Fourier d'une distribution de Dirac est la fonction constante 1 : l'amplitude de diffusion est indépendante de l'angle de diffusion 2θ. Par abus de langage, il est souvent dit que les neutrons « ne possèdent pas de facteur de diffusion atomique ».
Comme l'interaction est nucléaire, chaque isotope possède une amplitude de diffusion différente. La transformée de Fourier est proportionnelle à l'amplitude de l'onde sphérique, qui a la dimension d'une longueur. Ainsi, l'amplitude de diffusion caractérisant l'interaction d'un neutron avec un isotope donné est appelée « longueur de diffusion » . Elle est exprimée en femtomètres (fm). Les longueurs de diffusion neutroniques varient de façon erratique entre éléments voisins dans le tableau périodique et entre isotopes d'un même élément. Elles ne peuvent être déterminées qu'expérimentalement, car la théorie des forces nucléaires n'est pas adaptée pour calculer ou prédire la valeur de à partir des autres propriétés du noyau[13]. Les valeurs des longueurs de diffusion de neutrons thermiques (de longueur d'onde entre 1 Å et 4 Å) pour chaque isotope sont données par le National Institute of Standards and Technology[14] ainsi que dans les tables internationales de cristallographie[15].
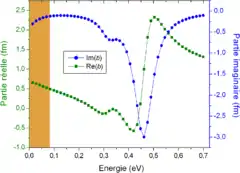
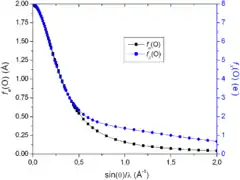
La longueur de diffusion est fortement dépendante de l'énergie des neutrons incidents, en particulier dans le cas des neutrons chauds (d'énergie supérieure à 0,1 eV, voir la figure). L'énergie des neutrons incidents nécessaire pour exciter le noyau est en général supérieure à celle utilisée dans les expériences de diffraction (entre 0,3 et 0,6 eV pour l'isotope 151Eu, par exemple), c'est la raison pour laquelle on observe peu d'effets de diffusion anomale avec les neutrons. Pour les quelques isotopes concernés, comme le 10B, n'est pas une grandeur réelle mais est complexe :
où décrit la variation en phase de la longueur de diffusion due à l'absorption de neutrons. Cette absorption donne ainsi lieu à de la diffusion incohérente. Dans la pratique, afin de simplifier l'analyse de données de diffraction de neutrons, il est possible de n'utiliser que des isotopes n'absorbant pas les neutrons lors de la synthèse du cristal, par exemple le 11B dans le cas du bore.
Interactions magnétiques
Bien que neutre, le neutron est un fermion et possède un spin. Lors de la diffusion de neutrons par de la matière condensée, la diffusion magnétique est due à l'interaction du spin du neutron avec les moments magnétiques (de spin et orbitaux) des électrons non appariés dans les orbitales externes de certains atomes : ce sont les électrons des sous-couches d pour les métaux de transition, 4f pour les terres rares et 5f pour les actinides. En général, une seule orbitale contribue à la diffusion magnétique. représente la distribution spatiale du moment magnétique de ces électrons non appariés autour du noyau. Comme les orbitales électroniques ont une taille comparable à la longueur d'onde des neutrons, le facteur de diffusion magnétique a une forme similaire à celui pour les rayons X. Cependant, cette diffusion magnétique n'a lieu qu'avec les électrons de valence, sans la contribution importante des électrons de cœur comme c'est le cas pour les rayons X.
Ainsi, au contraire de la diffusion nucléaire, l'objet diffusant lors de la diffusion magnétique est loin d'être une source ponctuelle et a même une taille effective plus grande que celle des objets diffusants pour les rayons X, ce qui conduit à une décroissance plus rapide du facteur de diffusion en fonction de [16]. Une autre différence avec la diffusion nucléaire est que le facteur de diffusion magnétique ne dépend pas des isotopes mais du degré d'oxydation des atomes.
En définissant l'opérateur densité de magnétisation qui donne le moment magnétique au point par unité de volume, le facteur de diffusion magnétique d'un atome s'écrit :
où représente un état quantique d'un atome. Pour un vecteur de diffusion nul, le facteur de diffusion magnétique est proportionnel au moment magnétique total de l'atome ou ion diffusant.
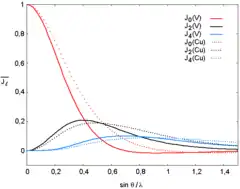
Dans le cas où une seule orbitale, de symétrie sphérique et de moment orbital bloqué, est responsable de la diffusion magnétique, le facteur de diffusion magnétique peut s'écrire[18] :
où est le facteur de Landé et les fonctions sont les intégrales radiales de la fonction d'onde radiale des électrons non appariés, définies par :
étant la fonction de Bessel sphérique d'ordre .
Dans le cas où le moment orbital des électrons n'est pas bloqué, le facteur de diffusion atomique est :
avec
étant le moment cinétique orbital, le spin électronique et le moment cinétique électronique total.
Si la symétrie de l'orbitale n'est pas sphérique, les intégrales radiales d'ordre supérieur à 2 doivent être prises en compte.
Cas des électrons
Les électrons interagissent avec les potentiels électrique et magnétique des atomes dans la maille du cristal et le facteur de diffusion atomique électronique en est la transformée de Fourier[19]. Au contraire de la diffusion de rayons X ou de neutrons, la distribution de potentiel n'est pas localisée autour d'un atome mais est une fonction continue de l'espace et dépend des autres atomes dans le cristal.
Il est cependant possible d'écrire la distribution de potentiel comme étant la somme de distributions individuelles des atomes aux positions :
Dans le cas des interactions électriques, qui sont les interactions prédominantes, la distribution de potentiel totale, périodique, est notée et l'onde diffusée est donnée par l'équation de Schrödinger indépendante du temps :
où est la masse relativiste des électrons incidents, la charge d'un électron et l'énergie cinétique de l'électron incident[20]. La correction relativiste de la masse des électrons est nécessaire, car le potentiel d'accélération des électrons utilisés en diffraction varie entre 10 et 400 kV, donnant lieu à des vitesses entre 20 % et 80 % de celle de la lumière, notée . En tenant compte de cette correction, la masse de l'électron et sa longueur d'onde sont :
où est la masse de l'électron au repos et β est le rapport /.
La résolution de l'équation de Schrödinger conduit à :
où représente l'onde incidente. Il s'agit d'une formule récurrente, puisque apparaît dans l'expression de l'intégrale. L'expression du facteur de diffusion atomique pour la diffusion d'électrons à partir de l'expression donnée dans la définition générale est donc beaucoup plus compliquée que dans le cas de la diffusion de rayons X.
Approximation de Mott
Les facteurs de diffusion atomique électroniques, , peuvent être calculés à partir de ceux pour les rayons X, , en utilisant la formule de Mott[9], sous l'approximation d'atomes isolés et sphériques :
où est le numéro atomique de l'atome ; est exprimé en Å. Cette formule prend en compte la diffusion élastique du nuage électronique ainsi que celle du noyau. Elle n'est plus valable aux très petits angles de diffusion : pour , comme , le numérateur et le dénominateur du second terme de s'annulent et la fonction diverge. Dans ce cas, la formule d'Ibers[22] est utilisée :
où est la moyenne du carré du rayon de l'atome.
Une expression alternative des formules de Moth et d'Ibers laissant apparaître la permittivité du vide est aussi trouvée dans la littérature[23] :
Interpolation
Les valeurs des facteurs de diffusion pour chaque atome et ion sont données pour entre 0 et 6 Å-1 dans les tables internationales de cristallographie[21]. Ces valeurs peuvent être interpolées par une somme de cinq gaussiennes[24] :
Les paramètres , , , , , , , , et sont également donnés dans les tables internationales de cristallographie.
Correction asphérique
Comme les rayons X, les électrons sont sensibles à la forme du nuage électronique des atomes via la distribution de potentiel . Les liaisons chimiques dans un cristal déforment la partie externe du nuage électronique, donnant lieu à une déviation de la sphéricité idéale. Dans ce cas, pour des angles de diffusion non proches de 0, la formule de Mott est toujours valable et est utilisée avec les valeurs de corrigées[25].
Notes et références
Notes
- Le vecteur de diffusion est ici une variable continue. Il est parfois noté dans la littérature afin d'éviter la confusion avec le vecteur de diffraction, utilisé dans la théorie de la diffraction sur un cristal. Cette confusion ne peut pas être faite ici car seule la diffusion d'une onde par un atome isolé est traitée. L'ensemble des vecteurs de diffraction est un sous-ensemble discret de celui des vecteurs de diffusion ne contenant que les vecteurs satisfaisant la condition de Laue.
- Dans le cadre de la diffraction de neutrons, un cristal contient pour chaque élément une certaine proportion d'isotopes, distribués aléatoirement dans le cristal : la longueur de diffusion moyenne de chaque élément est alors la somme d'un terme « cohérent » et d'un terme « incohérent » (voir l'article diffraction de neutrons). Cette partie incohérente de la longueur de diffusion n'est pas discutée ici car on ne s'intéresse qu'à la diffusion par un seul atome.
Références
- (en) D. McKie et C. McKie, Essentials of Crystallography, Oxford/Edinburgh/London etc., Blackwell Scientific Publications, , 437 p. (ISBN 0-632-01574-8)
- (en) W.L. Bragg et J. West, dans Zeitschrift für Kristallographie, vol. 69, 1930, p. 118
- (en) D.R. Hartree, « The Wave Mechanics of an Atom with a Non-Coulomb Central Field. Part I. Theory and Methods », Mathematical Proceedings of the Cambridge Philosophical Society, vol. 24, no 1, , p. 89-110 (DOI 10.1017/S0305004100011919)
- (en) D.R. Hartree, « The Wave Mechanics of an Atom with a non-Coulomb Central Field. Part III. Term Values and Intensities in Series in Optical Spectra », Mathematical Proceedings of the Cambridge Philosophical Society, vol. 24, no 3, , p. 426-437 (DOI 10.1017/S0305004100015954)
- (en) D.R. Hartree, « The Distribution of Charge and Current in an Atom consisting of many Electrons obeying Dirac's equations », Mathematical Proceedings of the Cambridge Philosophical Society, vol. 25, no 2, , p. 225-236 (DOI 10.1017/S0305004100018764)
- (en) L. Pauling, dans Proceedings of the Royal Society, vol. 114, 1927, p. 181
- (en) L. Pauling et I. Sherman, dans Zeitschrift für Kristallographie, vol. 81, 1932, p. 1
- (en) International Tables for Crystallography, vol. C : Mathematical, physical and chemical tables, E. Prince et NIST Center for Neutron Research, Kluwer Academic Publishers, , 3e éd. (ISBN 978-0-470-71029-6), chap. 6.1 (« Intensity of diffracted intensities »), p. 555-564 et 566-577
- (en) A.G. Fox, M.A. O'Keefe et M.A. Tabbernor, « Relativistic Hartree–Fock X-ray and electron atomic scattering factors at high angles », Acta Cryst. A, vol. 45, no 11, , p. 786-793 (DOI 10.1107/S0108767389007567)
- (en) International Tables for Crystallography, vol. B : Reciprocal space, U. Shmueli, Kluwer Academic Publishers, , 3e éd. (ISBN 978-1-4020-8205-4), chap. 1.2 (« The structure factor »), p. 14
- (en) C. Lecomte, B. Guillot, C. Jelsch et A. Podjarny, « Frontier example in experimental charge density research: Experimental electrostatics of proteins », International Journal of Quantum Chemistry, vol. 101, no 5, , p. 624-634 (DOI 10.1002/qua.20317)
- (en) J.E. Lynn, « The Energy Dependence of the Neutron Coherent Scattering Length of Europium », Journal of Applied Crystallography, vol. 22, , p. 476-482
- (en) Gordon Squires, Introduction to the Theory of Thermal Neutron Scattering, Dover Publications, (ISBN 0-486-69447-X), p. 260
- (en) « Neutron scattering lengths and cross sections », sur National Institute of Standards and Technology (consulté le )
- (en) International Tables for Crystallography, vol. C : Mathematical, physical and chemical tables, E. Prince et NIST Center for Neutron Research, Kluwer Academic Publishers, , 3e éd. (ISBN 978-0-470-71029-6), chap. 4.4 (« Neutron techniques »), p. 445-452
- (en) L. Dobrzynski et K. Blinowski, Neutrons and Solid State Physics, New York/London/Toronto etc., Ellis Horwood Limited, , 306 p. (ISBN 0-13-617192-3)
- (en) International Tables for Crystallography, vol. C : Mathematical, physical and chemical tables, E. Prince et NIST Center for Neutron Research, Kluwer Academic Publishers, , 3e éd. (ISBN 978-0-470-71029-6), chap. 4.4 (« Neutron techniques »), p. 454-460
- (en) Stephen W. Lovesey, Theory of neutron scattering from condensed matter, vol. 2, Oxford University Press, , 360 p. (ISBN 978-0-19-852029-0, lire en ligne), chap. 7 (« Principal features of magnetic scattering »)
- (en) John M. Cowley, Diffraction Physics, North-Holland Physics Publishing, (ISBN 0-444-86121-1), p. 78
- (en) International Tables for Crystallography, vol. C : Mathematical, physical and chemical tables, E. Prince et NIST Center for Neutron Research, Kluwer Academic Publishers, , 3e éd. (ISBN 978-0-470-71029-6), chap. 4.3 (« Electron diffraction »), p. 259
- (en) International Tables for Crystallography, vol. C : Mathematical, physical and chemical tables, E. Prince et NIST Center for Neutron Research, Kluwer Academic Publishers, , 3e éd. (ISBN 978-0-470-71029-6), chap. 4.3 (« Electron diffraction »), p. 263-285
- (en) James A.Ibers, « Atomic scattering amplitudes for electrons », Acta Cryst., vol. 11, no 3, , p. 178-183 (DOI 10.1107/S0365110X58000475)
- (en) Jiahu Wang, Vedene H. Smith Jnr, Carlos F. Bunge et Rocio Jáuregui, « Relativistic X-ray Elastic Scattering Factors for He-Ar from Dirac-Hartree-Fock Wave Functions », Acta Cryst. A, vol. 52, no 5, , p. 649-658 (DOI 10.1107/S0108767396003960)
- (en) L.M. Peng, G. Ren, S.L. Dudarev et M.J. Whelan, « Robust Parameterization of Elastic and Absorptive Electron Atomic Scattering Factors », Acta Cryst. A, vol. 52, no 2, , p. 257-276 (DOI 10.1107/S0108767395014371)
- (en) Jimpei Harada et Yasuzi Kashiwase, « Atomic Scattering Factor for Electrons of Atoms with Aspherical Charge Distribution », J. Phys. Soc. Jpn., vol. 17, , p. 829-838 (DOI 10.1143/JPSJ.17.829)
- (en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Atomic form factor » (voir la liste des auteurs).
Voir aussi
Articles connexes
Liens externes
- (en) « Atomic scattering factor », sur IUCr Online Dictionary of Crystallography (consulté le )






























![{\displaystyle \ln {\left[f_{0}\left({\frac {\sin {\theta }}{\lambda }}\right)\right]}\approx \sum _{i=1}^{3}a_{i}s^{i}.}](https://img.franco.wiki/i/1413299d6dcb33e40e4dc0ba49626be1e567755f.svg)














































![{\displaystyle {\begin{array}{rcl}g_{S}&=&\displaystyle {\frac {J(J+1)-L(L+1)+S(S+1)}{J(J+1)}}\\[2ex]g_{L}&=&\displaystyle {\frac {J(J+1)+L(L+1)-S(S+1)}{2J(J+1)}}\\[2ex]g&=&\displaystyle {1+{\frac {g_{S}}{2}}}\end{array}}}](https://img.franco.wiki/i/8d17c1547ea0bf16bca82cedd8ec1f48ca307a37.svg)








![{\displaystyle {\overrightarrow {\nabla }}^{2}\psi _{f}({\vec {r}})+{\frac {8\pi ^{2}me}{h^{2}}}\left[E+\varphi _{e}({\vec {r}})\right]\psi _{f}({\vec {r}})=0}](https://img.franco.wiki/i/083dc1ccaccc65ed01fc5b07faf588705524c214.svg)

















![{\displaystyle {\begin{array}{rcl}f_{e}({\vec {K}})&=&\displaystyle {{\frac {2\pi me^{2}}{h^{2}\epsilon _{0}}}{\frac {Z-f_{X}({\vec {K}})}{||{\vec {K}}||^{2}}}}\\[2ex]f_{e}({\vec {0}})&=&\displaystyle {{\frac {\pi me^{2}}{3h^{2}\epsilon 0}}\langle r^{2}\rangle }\end{array}}}](https://img.franco.wiki/i/0024ddaae896225a267889f861ad52ced339352b.svg)





