Fonction gaussienne
Une fonction gaussienne est une fonction en exponentielle de l'opposé du carré de l'abscisse (une fonction en exp(-x2)). Elle a une forme caractéristique de courbe en cloche.
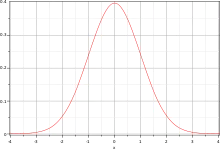
L'exemple le plus connu est la densité de probabilité de la loi normale
où μ est l'espérance mathématique et σ est l'écart type.
Propriétés des fonctions gaussiennes
Généralités
Les fonctions gaussiennes sont analytiques, de limite nulle en l'infini.
Largeur à mi-hauteur
La largeur à mi-hauteur H vaut
la demi-largeur à mi-hauteur vaut donc environ 1,177·σ.
Dérivation
La fonction gaussienne est infiniment dérivable partout. Les dérivées successives de la fonction gaussienne font apparaitre les polynômes d'Hermite.
Intégration
S'il est aisé de calculer les dérivées d'une fonction gaussienne, on ne peut pas écrire ses primitives à l'aide des fonctions élémentaires (c'est une conséquence d'un théorème de Liouville) ; on les exprime à l'aide de la fonction d'erreur. On peut cependant calculer l'intégrale d'une gaussienne sur la droite réelle, par l'intégrale de Gauss :
et, de manière générale :
Ainsi, cette intégrale vaut 1 si et seulement si , et alors, la gaussienne a les propriétés d'une densité de probabilité d'une variable aléatoire suivant une loi normale d'espérance μ et de variance σ2. Graphiquement "a" représente l'amplitude de la fonction gaussienne, son ordonnée maximale.
Les fonctions gaussiennes centrées en 0 minimisent le principe d'incertitude de Fourier.
Propriétés de deux fonctions gaussiennes
Soient deux fonctions gaussiennes et .
Somme de deux fonctions gaussiennes
La somme de ces deux fonctions ne se simplifie pas plus.
En revanche, si X1 et X2 sont des variables aléatoires gaussiennes indépendantes de densité de probabilité f1(x) et f2(x) respectivement, alors la variable aléatoire X = X1 + X2 est aussi gaussienne et sa densité de probabilité est donnée par le produit de convolution de f1(x) et f2(x).
Produit de convolution de deux fonctions gaussiennes
Le produit de convolution f = f1 * f2 de deux fonctions gaussiennes est encore une fonction gaussienne, de moyenne et d'écart-type . Dans le cadre des probabilités, il s'agit de la densité de probabilité de la somme de deux variables aléatoires indépendantes suivant des lois normales.
Produit de deux fonctions gaussiennes
Le produit de deux fonctions gaussiennes est encore une fonction gaussienne ; cependant, les propriétés de densité de probabilités ne sont pas conservées par le produit (le facteur de normalisation a n'étant pas forcément tel que l'intégrale vaille 1)[1]. Par exemple[1] le produit de deux fonctions gaussiennes de même paramètre μ = μ1 = μ2, a pour paramètres a = a1a2, μ et . Dans le cadre des probabilités, la densité de probabilité du produit de deux loi normales a une expression analytique faisant intervenir une fonction de Bessel[2].
Comme la fonction gaussienne est une fonction propre de la transformée de Fourier continue, on obtient par la formule sommatoire de Poisson :
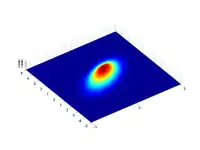
Fonction gaussienne en deux dimensions
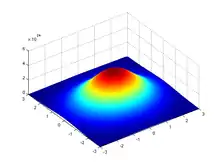
En deux dimensions, la fonction en exponentielle peut être toute forme quadratique définie négative. On en déduit que toute courbe d'iso-valeurs sera une ellipse.
Une forme particulière de fonction gaussienne 2D est :
où A est l'amplitude, x0,y0 est le centre et σx, σy définissent l'écartement selon x et y.
De manière générale, une fonction gaussienne 2D est de la forme :
où la matrice
est définie positive.
Signification des coefficients
En reprenant les notations de la forme générale, on remarque que A désigne la hauteur du sommet de la courbe, et (x0, y0) ses coordonnées.
En définissant :
alors la cloche tourne dans le sens horaire d'un angle θ (pour le sens trigonométrique, il suffit de prendre l'opposé de b). On peut le voir dans les exemples suivants :
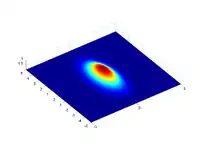 . |
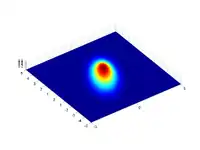 . |
 . |
Applications
Les fonctions gaussiennes sont très utilisées en physique. En effet, nombre de phénomènes physiques suivent une distribution de type gaussien, expliqué par le théorème central limite. L'intérêt des fonctions gaussiennes en physique est également dû à certaines de leurs propriétés mathématiques remarquables. Par exemple, la transformée de Fourier d'une fonction gaussienne est une fonction gaussienne, ce qui entraîne notamment le fait que les faisceaux lasers sont des faisceaux gaussiens.
Références
- (en) P. Bromiley, « Products and convolutions of gaussian probability density functions », Tina-Vision Memo, no 3, (lire en ligne).
- B. Sorin et P. Thionet, « Lois de probabilités de Bessel », Revue de statistique appliquée, no 16.4, , p. 65-72 (lire en ligne [PDF]).
Voir aussi
Articles connexes
- Intégrale de Gauss
- Loi normale
- Noyau de la chaleur
- Transformation de Weierstrass
- Autres courbes en cloche :
Sites externes
- Jean-Pierre Kahane, « La courbe verte en cloche » sur Images des mathématiques, CNRS, 2019.













![{\displaystyle f(x,y)=A\exp \left[-\left({\frac {(x-x_{0})^{2}}{2\sigma _{x}^{2}}}+{\frac {(y-y_{0})^{2}}{2\sigma _{y}^{2}}}\right)\right].}](https://img.franco.wiki/i/f1a0e18291eadb4d829f76e83c76e14e2300354f.svg)
![{\displaystyle f(x,y)=A\exp \left[-\left(a(x-x_{0})^{2}+2b(x-x_{0})(y-y_{0})+c(y-y_{0})^{2}\right)\right]}](https://img.franco.wiki/i/5457386ce4fd89244d5614d3b37d883a85d6a1ba.svg)
![\left[{\begin{matrix}a&b\\b&c\end{matrix}}\right]](https://img.franco.wiki/i/74769e46229529b2f5710c4abe3c8906984fe35f.svg)





