Transformation de Weierstrass
En analyse, la transformée de Weierstrass[1] d'une fonction f : ℝ → ℝ, du nom de Karl Weierstrass, est une version "lissée" de f (x) obtenue en moyennant les valeurs de f, pondérées avec une courbe gaussienne centrée en x.
La fonction, notée F, est définie par
la convolution de f avec la fonction gaussienne
Le facteur 1/ √4π est choisi pour des raisons de normalisation, la gaussienne étant ainsi d'intégrale égale à 1 et les fonctions constantes ne sont pas changées par la transformation de Weierstrass.
On pourra aussi utiliser la notation W[f](x). La transformée F (x) n'est pas nécessairement définie pour tout x, où l'intégrale ne converge pas.
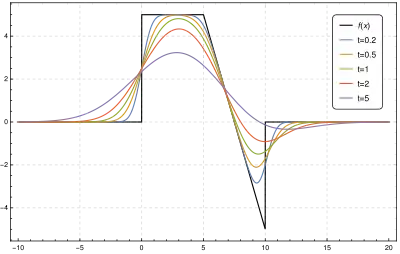
La transformation de Weierstrass est intimement liée à l'équation de la chaleur (ou, plus généralement, l'équation de diffusion avec coefficient de diffusion constant). Si la fonction f décrit la température initiale en chaque point d'une poutre infiniment longue de conductivité thermique égale à 1, alors la distribution thermique de la poutre au temps t = 1 sera donnée par la fonction F. En faisant varier les valeurs de t, on peut construire une transformée généralisée de Weierstrass de f.
La transformation généralisée de Weierstrass donne un moyen d'approcher une fonction intégrable f donnée arbitrairement avec des fonctions analytiques.
Désignations
Weierstrass a utilisé cette transformation dans sa preuve originale du théorème d'approximation de Weierstrass. Elle est également appelée transformation de Gauss ou de Gauss–Weierstrass du nom de Carl Friedrich Gauss et aussi transformation de Hille d'après Einar Carl Hille qui l'a étudié en profondeur. La généralisation Wt mentionnée supra est connue en traitement du signal comme un filtre de Gauss et en traitement de l'image (quand définie sur ) comme un flou gaussien.
Transformées de fonctions particulières
Toute fonction constante est également à sa transformée de Weierstrass.
La transformée de Weierstrass d'un polynôme est un polynôme de même degré. En effet, si Hn désigne le polynôme d'Hermite (physique) de degré n, alors la transformée de Weierstrass de Hn(x/2) est égale à xn. On peut le voir en utilisant le fait que la fonction génératrice des polynômes d'Hermite est proche du noyau gaussien utilisée dans la définition de la transformée de Weierstrass.
La transformée de Weierstrass de la fonction eax (avec a une constante arbitraire) est ea2 eax. Les fonctions exponentielles de la forme eax sont donc des fonctions propres de la transformation de Weierstrass. (Cette propriété est, en fait, vraie pour toutes les transformations basées sur une convolution.)
En posant a=bi avec i l'unité imaginaire, et grâce à l'identité d'Euler, on peut vérifier que les transformées de Weierstrass de fonction cos(bx) est e−b2 cos(bx) et celle de sin(bx) vaut e−b2 sin(bx).
La transformée de Weierstrass de la fonction eax2 est
- vraie si a < 1/4 et non définie sinon.
En particulier, en choisissant a négatif, il est évident que la transformée de Weierstrass d'une gaussienne est une autre gaussienne, mais plus large.
Propriétés générales
La transformation de Weierstrass qui associe une fonction f à une fonction F est linéaire et invariante par translation : la transformée de f(x + a) est F(x + a).
Si la transformée F(x) est bien définie pour les réels x = a et x = b, alors il existe pour toutes les valeurs comprises entre elles et y forme une fonction analytique ; plus encore, F(x) existe pour tout complexe x tel que a ≤ Re(x) ≤ b et forme une fonction holomorphe sur cette bande du plan complexe. C'est la traduction précise de la propriété de "lissage" de la transformation.
Si f est intégrable sur toute la droite réelle (i.e. f ∈ L1(ℝ)), sa transformée de Weierstrass F l'est également, de plus, si f est positive, F aussi et leurs intégrales sur ℝ sont égales. On retrouve ainsi la propriété physique que l'énergie thermique totale est conservée par l’équation de la chaleur, ou que la quantité totale de matériau diffusant est conservé par l'équation de diffusion.
Par la suite, il vient que pour 0 < p ≤ ∞ et f ∈ Lp(ℝ), alors F ∈ Lp(ℝ) et ||F||p ≤ ||f||p. La transformée de Weierstrass permet de définir un opérateur borné W : Lp(ℝ) → Lp(ℝ).
Si f est assez régulière, alors la transformée de Weierstrass de la dérivée d'ordre k de f est égale à la dérivée d'ordre k de la transformée de Weierstrass de f.
On peut relier la transformation de Weierstrass W et la transformée bilatérale de Laplace L. En notant
alors
Filtre passe-bas
D'après les remarques précédentes, on peut dire que du point de vue du traitement du signal, pour un signal f contenant la fréquence b (i.e. contenant une combinaison linéaire de sin(bx) et cos(bx)), sa transformée de Weierstrass F contiendra la même fréquence, mais avec une amplitude multipliée par un facteur e−b2. Ainsi, les fréquences hautes seront plus réduites que les fréquences basses, donc la transformation de Weierstrass agit comme un filtre passe-bas, une propriété analogue à la transformation de Fourier. On sait que la transformation de Fourier analyse un signal à travers ses fréquences, transforme les convolutions en produits, et les gaussiennes en gaussiennes. La transformation de Weierstrass est une convolution avec une gaussienne et doit donc être vu comme une multiplication du signal transformé Fourier avec une Gaussienne, qui subit une transformation inverse de Fourier. C'est cette multiplication avec une gaussienne en fréquence qui atténue les hautes fréquences, et permet de retrouver les propriétés régularisantes de la transformation de Weierstrass.
Transformée inverse
La formule qui suit, proche de la transformée de Laplace d'une gaussienne, et un analogue réel de la transformation de Hubbard-Stratonovich (en), est assez simple à établir :
En remplaçant u par l'opérateur formel de dérivation D=d⁄dx et en utilisant l'opérateur de décalage de Lagrange
- ,
(cette égalité se déduit de la série de Taylor de l'exponentielle), on a
ce qui permet de déduire une expression formelle de la transformation de Weierstrass W,
où l'opérateur est à comprendre comme agissant sur f (x) comme
L'égalité précédente dépend de propriétés de convergence non précisées, et l'égalité W=eD2 n'est donc pas toujours vérifiée ; ainsi, il existe des fonctions f dont la transformée de Weierstrass est bien définie, mais pour lesquelles eD2f(x) n'a aucun sens.
Elle est cependant utile et permet de trouver rapidement les transformées de Weierstrass de fonctions usuelles simples, comme les polynômes, les fonctions exponentielles et trigonométriques.
L'opérateur inverse formel de la transformation de Weierstrass est donc donné par
Une fois encore, la formule est vérifiée sous réserve de propriétés de convergence et ne peut que servir de guide. Elle est vraie pour certaines classes de fonctions si l'opérateur donné dans le membre droit est bien défini[2].
On peut, par un autre moyen, essayer d'inverser la transformée de Weierstrass : d'une fonction analytique donnée
on applique W−1 pour obtenir
avec les polynômes d'Hermite (physiques) Hn.
Cette formule de f(x) reste un indicateur formel, vraie si la série à droite converge. Mais si, par exemple, f ∈ L2(ℝ), alors il suffit de connaître les valeurs des dérivées de F en x = 0 pour obtenir les coefficients an, et donc reconstruire f comme une série de polynômes d'Hermite.
Une troisième méthode d'inversion consiste à utiliser l'égalité faisant intervenir la transformation de Laplace donnée supra, dont on connait la formule d'inversion. Le résultat est donné dans la suite pour les distributions.
Généralisations

Le noyau de convolution peut être remplacé par le noyau gaussien (pour t > 0) au lieu de , qui permet de définir l'opérateur Wt de la transformation généralisée de Weierstrass.
Pour les petites valeurs de t, Wt[f] est très proche de f, mais régulière. Plus t est grand, plus l'opérateur va moyenner et changer les variations de f. Physiquement, Wt revient à suivre l'évolution de l'équation de la chaleur (ou de diffusion) avec t correspondant au temps, avec une propriété additive,
qui se traduit par « diffuser pendant une durée t, puis pendant une durée s, est équivalent à diffuser pendant une durée s + t ». On peut étendre l'idée en définissant à t = 0 l'opérateur W0 qui est l'opérateur identité (le noyau devenant alors une distribution de Dirac), et construisant ainsi un semi-groupe d'opérateurs.
Le noyau de la transformation généralisée de Weierstrass est parfois appelé noyau de Gauss–Weierstrass, et est la fonction de Green de l'équation de diffusion sur ℝ.
Wt peut être écrit à partir de W : pour une fonction f(x), on définit une nouvelle fonction ft(x) = f(x√t), puis on pose Wt[f](x) = W[ft](x/√t), une conséquence de la règle de substitution.
La transformation de Weierstrass peut également être définie pour certaines classes de distributions ou "fonctions généralisées"[3]. Par exemple, la transformée de Weierstrass d'une fonction delta de Dirac est la gaussienne .
Dans ce contexte, des formules d'inversion plus rigoureuses peuvent être prouvées :
où x0 est un réel donnée pour lequel F(x0) existe, l'intégrale s'étend autour de la ligne verticale de plan complexe de partie réelle x0, et cette limite est à voir au sens des distributions.
Partant de là, la transformation de Weierstrass peut être définie pour des fonctions à valeurs réelles ou complexes définies sur ℝn. Il suffit de poser la convolution sur ℝn et de considérer le terme (x − y)2 comme le carré de la norme euclidienne du vecteur x − y; le facteur constant devant l’intégrale est également à ajuster pour retrouver une gaussienne d'intégrale égale à 1.
Plus généralement, la transformation de Weierstrass peut être définie sur une variété riemannienne : l'équation de la chaleur peut y être formulée (par l'opérateur de Laplace-Beltrami sur la variété), et la transformée de Weierstrass W[f] est alors donnée en suivant la solution de l'équation de la chaleur dans le temps, avec comme solution initiale une "distribution de température" f.
Liens avec d'autres transformations
En considérant la convolution avec le noyau 1/(π(1 + x2)) au lieu d'une gaussienne, on trouve la transformation de Poisson qui a des propriétés de régularisation et moyennage similaires.
Voir aussi
- Flou gaussien
- Filtre de Gauss
- Q-représentation Husimi
Références
- (en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Weierstrass transform » (voir la liste des auteurs).
- Ahmed I. Zayed, Handbook of Function and Generalized Function Transformations, Chapter 18. CRC Press, 1996.
- (en) G. G. Bilodeau, « The Weierstrass Transform and Hermite Polynomials », Duke Mathematical Journal, vol. 29, , p. 293-308 (lire en ligne)
- Yu A. Brychkov, A. P. Prudnikov. Integral Transforms of Generalized Functions, Chapter 5. CRC Press, 1989





={\frac {1}{\sqrt {4\pi }}}\mathrm {e} ^{-x^{2}/4}L[g]\left(-{\frac {x}{2}}\right).}](https://img.franco.wiki/i/10cb8dd82d912c7a84cfab9287bfc3fa26e0ac94.svg)


\end{aligned}}}](https://img.franco.wiki/i/1e48955b09049666ea15b28a9917ddf7dcc879f4.svg)




![{\displaystyle f(x)=W^{-1}[F(x)]=\sum _{n=0}^{\infty }a_{n}W^{-1}[x^{n}]=\sum _{n=0}^{\infty }a_{n}H_{n}(x/2)}](https://img.franco.wiki/i/0105c2f9e4438e3c24d8dd3c94665c1638095ac4.svg)




