Histoire des nombres complexes

Girolamo Cardano est le premier mathématicien à imaginer l’existence de racines carrées de nombres négatifs (1545).

Les nombres complexes sont nés de confrontations avec des opérations impossibles comme les racines carrées de nombres négatifs. Un des premiers mathématiciens à en imaginer l'existence[note 1] est Cardan en 1545 dans son Artis magnae sive regulis algebraicus[1] à l'occasion de la résolution de l'équation

${\displaystyle x(10-x)=40}$

dont il donne les solutions sous la forme suivante :

que l'on peut lire comme

${\displaystyle 5+{\sqrt {-15}}\quad {\text{et}}\quad 5-{\sqrt {-15}}\ }$

et fait observer que le produit de ces deux nombres donne bien 40 tout en reconnaissant que l'équation est, en toute théorie, impossible à résoudre. Il demande au lecteur de faire preuve d'imagination et appelle ces nombres des quantités sophistiquées. Selon Remmert[2], on ne sait pas si Cardan, en inventant cette écriture, songe particulièrement à résoudre l'équation de degré trois. Mais cet outil va vite s'y révéler très utile. En effet, les formules de Cardan dans la résolution de l'équation

${\displaystyle x^{3}+px+q=0}$

consistent à faire la somme des racines cubiques des deux solutions de l'équation du second degré

${\displaystyle X^{2}+qX-{\frac {p^{3}}{27}}=0.}$

Cela nécessite que le discriminant de cette seconde équation soit positif. Or, justement dans le cas où l'équation initiale du troisième degré possède trois solutions réelles, ce discriminant est négatif. Ce qui conduit à la situation paradoxale suivante : quand il y a pléthore de racines, la méthode de Cardan ne peut pas s'appliquer, à moins d'accepter de quitter temporairement le domaine du possible et de travailler sur des nombres imaginaires utilisant des racines carrées de nombres négatifs.

La première formalisation avec règles de calcul sur ces quantités est l'œuvre de Raphaël Bombelli en 1572 dans son Algebra. C'est, selon Dominique Flament, le créateur indiscutable de la théorie des nombres imaginaires[3]. À côté des signes + et – qu'il appelle piu et meno, il invente deux autres signes, sortes d'opérateurs[4] qui symbolisent l'ajout ou le retrait d'une racine d'un nombre négatif : piu di meno et meno di meno. Ainsi l'expression que l'on note aujourd'hui 2 + i √121 est notée par Bombelli 2 piu di meno R.q. 121. Il évite ainsi la notation troublante que serait √–121. Il définit alors une règle des signes sur le produit de deux quelconques de ces quatre signes. Ainsi, par exemple, meno via meno fà piu (– par – donne +), piu di meno via meno fà meno di meno (+i par – donne –i) et piu di meno via piu di meno fa meno (+i par +i donne –). Il qualifie les quantités qu'il manipule de plus sophistiquées que réelles[5] mais les utilise pour résoudre l'équation du troisième degré

${\displaystyle x^{3}=15x+4}$

ce qui l'oblige à trouver les racines cubiques des quantités

${\displaystyle 2\pm 11~\mathrm {i} .}$

C'est ainsi qu'il présente sans expliquer sa méthode 2 ± i comme racine cubique de 2 ± 11 i. Selon Study, Bombelli aurait trouvé ce résultat par tâtonnements sans mettre au point de méthode générale[6].

René Descartes les baptise « nombres imaginaires » (1637).

Malgré le travail de ces deux précurseurs, à la fin du XVI^e siècle, ces quantités sophistiquées restent boudées par certains mathématiciens. Ainsi François Viète et Thomas Harriot refusent toute existence aux quantités tant négatives qu'imaginaires[7] et c'est en utilisant la trisection de l'angle que Viète résout l'équation de degré 3[7]. Simon Stevin, quant à lui, les juge inutiles[8].

Cependant la découverte de ces quantités semble lever l'obstacle des résolutions impossibles des équations de degré deux et de degré quatre. La question naturelle qui se pose est alors : peut-on, à condition d'accepter d'écrire des racines carrées de nombres négatifs, obtenir toujours n racines à un polynôme de degré n ? C'est la recherche d'une preuve du théorème fondamental de l'algèbre qui va durer deux siècles. Énoncé par Peter Rothe en 1608, par René Descartes et Albert Girard en 1627 et 1629, il est l'objet d'une démonstration qui semble aboutie chez Jean le Rond D'Alembert en 1746 ; il ne sera démontré par Carl Friedrich Gauss de manière rigoureuse qu'en 1799[9].

Dans son Invention nouvelle, Girard utilise sans état d'âme ces quantités qu'il appelle solutions enveloppées[note 2] pour résoudre l'équation x⁴ = 4 x + 3 et, à la question « À quoi servent-elles ? », il répond qu'elles permettent de montrer la véracité de la règle (un polynôme de degré 4 possède exactement 4 racines)[10]. Quant à Descartes, s'il n'apporte pas de contribution significative à cette nouvelle théorie qu'il n'accepte qu'avec réticence[11], il joue un rôle marquant par sa notoriété : en les citant dans ses écrits, il leur confère un statut officiel à tel point que le qualificatif d’imaginaire dont il les baptise dès 1637 devient leur nom officiel jusqu'en 1831. Cependant, cet adjectif rend bien compte du statut de ces nombres au milieu du XVII^e siècle : ils sont, certes, utiles mais on s'en méfie car on ne leur accorde aucune réalité[12].

Un siècle après leur naissance, les quantités imaginaires commencent à être utilisées par de nombreux mathématiciens. On cherche alors à spécifier leurs règles de calcul et à en isoler la partie réelle. À cette époque encore, un nombre imaginaire se note a ± √–b sans que soit privilégié √–1[13] et la notation rigoureuse de Bombelli n'a pas résisté à la mise en place de la notation symbolique de Viète et Descartes. Sous cette forme, les additions et les multiplications sont simples, les produits et quotients aussi quoique la présence d'une racine carrée négative puisse entraîner certaines erreurs : ainsi voit-on encore, sous la plume d'Euler en 1768[14] la règle suivante : √–1√–4 = √4 alors que la notation de Bombelli piu di meno R.q. 1 via piu di meno R.q.4 aurait donné meno R.q.4[note 3].

La difficulté se présente dans l'extraction de la racine n-ième d'un nombre complexe. Cette opération est nécessaire, par exemple pour exhiber les solutions réelles d'une équation de degré 3. Or il se trouve qu'effectivement, il n'est pas possible, en général, d'exprimer les racines d'un polynôme de degré trois en utilisant des radicaux réels[15] et que le passage par une trisection d'angle se révèle souvent utile. Gottfried Wilhelm Leibniz se méfie beaucoup de ces « monstres du monde des idées »[note 4] et cherche à les faire disparaître dans des expressions comme ⁿ√a+ib + ⁿ√a–ib en utilisant sa formule du binôme dès 1675[16]. Son idée est reprise et développée en 1738 par François Nicole[17], qui donne ainsi la formule suivante[18] :

${\displaystyle {\begin{aligned}{\frac {1}{2}}\left({\sqrt[{3}]{{\frac {a}{b}}+\mathrm {i} }}+{\sqrt[{3}]{{\frac {a}{b}}-\mathrm {i} }}\right)=&\left({\frac {a}{b}}\right)^{1/3}-{\frac {(1).(-2)}{2!.3^{2}}}\left({\frac {a}{b}}\right)^{-5/3}\\\ &+{\frac {(1).(-2).(-5).(-8)}{4!.3^{4}}}\left({\frac {a}{b}}\right)^{-11/3}-{\frac {(1).(-2).(-5).(-8).(-11).(-14)}{6!.3^{6}}}\left({\frac {a}{b}}\right)^{-17/3}+\cdots \end{aligned}}}$.

À cette époque, on ne se préoccupe pas de la convergence des séries proposées et on généralise les formules vues sur des quantités réelles selon le principe de permanence[19].

La démarche suivie par Abraham de Moivre en 1706 est autre : il établit un lien entre l'extraction d'une racine n-ième et la division d'un arc en n parties égales[16], publie en 1730 la formule

${\displaystyle \cos B={\frac {1}{2}}\left({\sqrt[{n}]{\cos(nB)+\mathrm {i} \sin(nB)}}+{\sqrt[{n}]{\cos(nB)-\mathrm {i} \sin(nB)}}\right)}$[note 5]

et affirme, dès 1738, que ⁿ√a+ib possède n valeurs distinctes, s'appuyant sur les n valeurs de ⁿ√cos(B) + i sin(B) obtenues sous la forme cos(B/n+kC/n) + i sin(B/n+kC/n) où C est une circonférence complète[20]. Il met également en pratique cette technique pour résoudre[21] l'équation de degré 5 : 5y–20y³+6y⁵ = ⁶¹⁄₆₄.

Le cas de l'exponentielle d'un complexe se révèle moins problématique. Euler, en 1740, par calcul de limite, établit que :

${\displaystyle \cos(x)={\frac {\exp(\mathrm {i} x)+\exp(-\mathrm {i} x)}{2}}\quad {\text{et}}\quad \sin(x)={\frac {\exp(\mathrm {i} x)-\exp(-\mathrm {i} x)}{2\mathrm {i} }}}$

puis en 1748, énonce sa formule :

${\displaystyle \cos(x)+\mathrm {i} \sin(x)=\mathrm {e} ^{\mathrm {i} x}.}$

Dans la foulée, il exprime ce que vaudrait l'exponentielle d'un nombre complexe, le sinus, le cosinus et la tangente d'un complexe ainsi que leurs fonctions réciproques[23].

Leonhard Euler fait l’inventaire de tous les calculs réalisables avec les nombres complexes. Il est à l’origine de la notation i (1777).

Le cas du logarithme d'un nombre complexe va occuper les mathématiciens Jean I^er Bernoulli, Leibniz, Euler et d'Alembert pendant près d'un demi-siècle[24]. En 1702, Bernoulli et Leibniz décomposent les fonctions rationnelles en éléments simples et les intègrent grâce à la fonction logarithme[25]. Ainsi, pour x > 1,

${\displaystyle \int {\frac {2}{x^{2}-1}}~\mathrm {d} x=\int \left({\frac {1}{x-1}}-{\frac {1}{x+1}}\right)~\mathrm {d} x=\ln(x-1)-\ln(x+1)+C=\ln \left({\frac {x-1}{x+1}}\right)+C.}$

La tentation est grande de généraliser le processus à des dénominateurs dont les racines sont complexes[25] :

${\displaystyle {\begin{aligned}\int {\frac {2}{x^{2}+1}}~\mathrm {d} x&={\frac {1}{\mathrm {i} }}\int \left({\frac {1}{x-\mathrm {i} }}-{\frac {1}{x+\mathrm {i} }}\right)~\mathrm {d} x={\frac {1}{\mathrm {i} }}\left(\ln(x-\mathrm {i} )-\ln(x+\mathrm {i} )\right)+C\\\ &={\frac {1}{\mathrm {i} }}\ln \left({\frac {x-\mathrm {i} }{x+\mathrm {i} }}\right)+C={\frac {1}{\mathrm {i} }}\ln \left({\frac {x^{2}-1}{x^{2}+1}}-\mathrm {i} {\frac {2x}{x^{2}+1}}\right)+C.\end{aligned}}}$

Encore faut-il savoir ce que peut valoir ln(a+ib). En 1714, Roger Cotes établit l'égalité[26] :

${\displaystyle \mathrm {i} x=\ln(\cos x+\mathrm {i} \sin x)}$

mais ces expressions, utilisées sans précaution selon le principe de permanence[19], produisent rapidement des incohérences, en particulier sur la définition de ln(–1), que Bernoulli s'obstine à vouloir nul malgré les remarques de Leibniz lui faisant remarquer que, ln(i) valant i π/2, ln(i²) devrait valoir i π. Cette controverse est résolue par Euler, en 1749, dans un texte célèbre, De la controverse entre Mrs Leibniz et Bernoulli sur les logarithmes des nombres négatifs et imaginaires[27] : il existe une infinité de valeurs possibles pour le logarithme d'un nombre complexe, toutes différant de ikC où C est une circonférence complète. Seuls les réels positifs possèdent un de leurs logarithmes réel et celui-ci correspond au logarithme classique. La formule générale est plus précisément :

${\displaystyle \ln(a+\mathrm {i} b)=\ln({\sqrt {a^{2}+b^{2}}})+\mathrm {i} \theta }$

où θ correspond à tout angle dont le cosinus vaut ${\textstyle a/{\sqrt {a^{2}+b^{2}}}}$ et le sinus ${\textstyle b/{\sqrt {a^{2}+b^{2}}}}$.

Cette définition lui permet de compléter la liste des calculs sur les nombres complexes par la puissance complexe d'un nombre complexe, expression multiforme comme l'est le logarithme d'un complexe :

${\displaystyle (a+\mathrm {i} b)^{u+\mathrm {i} v}=\mathrm {e} ^{(u+\mathrm {i} v)\cdot \ln(a+\mathrm {i} b)}.}$

Ainsi précise-t-il que les valeurs de (cos x + i sin x)^{n i} sont toujours réelles pour x réel et valent e^–nx+2kπn. Il précise une des valeurs de i ⁱ :

${\displaystyle \mathrm {i} ^{\mathrm {i} }=\mathrm {e} ^{-\pi /2}.}$

En 1777, Euler s'affranchit de la dernière notation ambiguë en remplaçant √–1 par la lettre i[28]. Euler pense ainsi avoir fait le tour de toutes les fonctions applicables à la variable complexe et avoir prouvé que le résultat de tout calcul sur des complexes à l'aide de fonctions connues à l'époque peut s'écrire sous forme a + ib, normalisant ainsi l'écriture de ceux-ci[29]. Il pense également avoir démontré le théorème fondamental de l'algèbre en prenant pour acquis deux résultats[30] : un polynôme de degré impair possède toujours une racine réelle[note 6] et toute racine d'un polynôme s'exprime à l'aide de radicaux à partir des coefficients du polynôme[note 7].

À la fin du XVIII^e siècle, on utilise les quantités imaginaires comme outils pratiques tant en analyse qu'en algèbre mais le caractère irréel de la racine carrée de –1 reste un problème. Les quantités imaginaires ne sont pas totalement acceptées par la communauté mathématique mais seulement tolérées[31]. L'étape suivante consiste à établir une construction des complexes qui leur permette d'entrer de plain-pied dans le corpus mathématique. Elle va se faire dans plusieurs directions, l'une géométrique, l'autre par l'algèbre abstraite.

Représentation géométrique par des vecteurs ou des points du plan

Correspondance ligne et complexe :OA ∼ a+ib = r.e^iθ

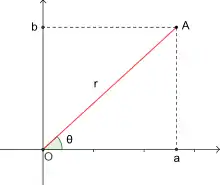
Cette association entre complexes et géométrie plane semble être dans l'air du temps dès le XVIII^e siècle. Ainsi voit-on Euler indiquer, en 1749, pour la recherche d'un antécédent pour la fonction logarithme d'un nombre « simplement imaginaire » ig, la méthode suivante[32] : prendre un arc de cercle égal à g et de rayon 1, déterminer le sinus et le cosinus de g, le nombre cherché sera cos g + i sin g. Selon Remmert[33], ceci est un indice très fort pour penser qu'Euler avait déjà fait le rapprochement entre point du plan et complexe. Certaines tentatives datent même du XVII^e siècle mais elles échouent toutes sur le sens à donner au produit de deux nombres complexes. John Wallis se heurte à ce problème dès 1685[34] dans A treatise of algebra et Heinrich Kühn (1690-1769) en 1750. En effet, selon Flament[35], imaginer que le produit de deux lignes puisse donner une ligne et non une surface est une idée révolutionnaire.

Définition de la somme : OC=OA+OB si et seulement si OACB est un parallélogramme.

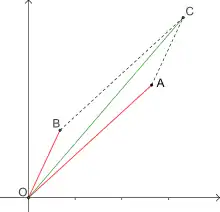
Les premières représentations des nombres complexes par des lignes dirigées sont les œuvres de deux praticiens : Caspar Wessel est un arpenteur et l'un de ses buts avoués est d'utiliser les complexes pour résoudre des triangles et manipuler des lignes possédant une longueur et une direction[31] ; quant à Jean-Robert Argand, il consacre une grande partie de son essai à montrer les intérêts pratiques de sa méthode[36]. Ils travaillent tous deux sur des lignes dirigées (on dirait aujourd'hui des vecteurs) avec une différence cependant : les lignes de Wessel ont toutes même origine alors qu'elles sont flottantes chez Argand. La somme de deux lignes dirigées se fait en utilisant la relation de Chasles et la multiplication se construit, une unité étant choisie, à l'aide de triangles semblables.

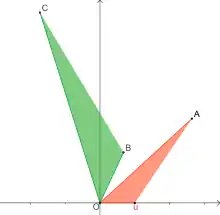Définition du produit : OC=OA×OB si et seulement si les triangles uOA et BOC sont directement semblables.

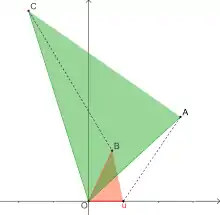Commutativité du produit : les triangles uOA et BOC sont semblables si et seulement si les triangles uOB et AOC le sont.

Mais les écrits de Wessel et d'Argand diffèrent dans leur esprit : Wessel construit une addition et une multiplication sur les lignes dirigées et a presque en tête la notion de structure algébrique, il associe à la ligne dirigée u le nombre 1 et trouve deux lignes dirigées v dont le carré vaut –1, la ligne dirigée obtenue en tournant dans le sens direct est appelée ε, et c'est seulement ensuite qu'il associe à chaque ligne dirigée un complexe. Argand, quant à lui, construit i comme moyenne géométrique entre la ligne 1 et la ligne –1, il définit alors un axe principal, l'axe des réels, un axe secondaire, ou médian, et construit chaque complexe comme somme d'une ligne sur l'axe principal et d'une ligne sur l'axe médian. Il caractérise également chaque ligne dirigée par sa longueur, qu'il appelle module de a + b√–1 et par l'angle qu'elle forme avec la ligne unité, et montre que le produit sur les complexes consiste à prendre la ligne dont la longueur est le produit des longueurs et l'angle la somme des angles. Tous deux tentent en vain de créer une correspondance analogue entre des objets de l'algèbre et les lignes dirigées de l'espace.

D'après Cauchy, Henri Dominique Truel aurait proposé une représentation géométriques des complexes dès 1786 mais le texte est perdu. Le papier de Wessel, daté de 1797, n'eut aucun succès parmi ses contemporains. Le travail de Wessel est totalement ignoré pendant près d'un siècle, mentionné seulement par Jürgensen en 1843 parmi d'autres mémoires de l'Académie jugés sans grande importance scientifique, et c'est quasiment par hasard qu'il est mentionné dans une thèse de Christensen (Mathematikens udrikling i danmark oy Norge i det 18-aarkundrede, Odense, 1896) qui le tire définitivement de l'oubli. Il est alors publié en français en 1897. Argand écrit le sien en 1806, ignorant les travaux de Wessel. Il envoie son essai à Adrien-Marie Legendre, qui l'envoie à François Français. Le texte est découvert par Jacques Frédéric Français, frère du précédent, qui le publie en 1813. Jacques Frédéric Français, grâce à davantage de formalisme, améliore la rigueur des résultats exposés par Argand[37]. Il est également à l'origine d'une notation privilégiant les éléments caractéristiques de la ligne dirigée : si sa longueur est r et l'angle qu'elle forme avec la direction principale est θ, il la note r_θ – le complexe √–1 s'écrit alors 1_+π/2 – puis il énonce les égalités : r_θ = re^θ√–1 = r cosθ + r sinθ √–1. Dans les tentatives de cette époque, on peut également citer l'« algèbre langue »[38] de l'abbé Adrien-Quentin Buée (1748-1826) en 1806 et les essais de John Warren[39] et de C. V. Mourey[40] en 1828, Vallès (1813), Bellavitis (1832)[41], Faure, De Gap (1845), Saint-Venant, Scheffler (de)[42], Siebeck[43], Dillner[44]…

Carl Friedrich Gauss popularise la représentation des complexes par des points et leur donne le nom de nombre complexe (1831).

Ces différents écrits rencontrent peu d'écho chez les mathématiciens de renom. Ainsi François-Joseph Servois écrit en 1813 qu'il n'y voit qu'un « masque géométrique appliqué sur des formes analytiques dont l'usage immédiat (est) plus simple et plus expéditif »[45]. Quant aux mathématiciens de l'école anglaise qui cherche, à cette époque, à faire sortir l'algèbre du carcan géométrique qui selon eux la pollue, ils ne peuvent que rejeter, par la voix de George Peacock, cette explication géométrique des complexes[46].

C'est grâce à Carl Friedrich Gauss que cet aspect des nombres complexes gagne ses lettres de noblesse. Gauss, mathématicien rigoureux et prudent, a publié avec parcimonie. Il est l'auteur de la première démonstration rigoureuse du théorème fondamental de l'algèbre. Dès 1797, il associe au point de coordonnées (a, b) le complexe a + ib ce qui, selon Bourbaki[47], serait un signe que dès cette époque, il avait conscience de cette correspondance possible, soupçon que confirme une lettre de Gauss à Bessel datée de 1811 où il précise cette correspondance[48]. C'est également lui qui popularise la notation d'Euler de i pour √–1, symbole qu'il utilise dès 1801[49] dans ses Disquisitiones arithmeticae, et qu'il nomme « unité imaginaire »[50]. C'est dans son ouvrage de 1831, Theoria residuorum biquadraticorum[51], qu'il présente son plan complexe qui est un plan formé de points et non de vecteurs. C'est aussi dans cet ouvrage qu'il rebaptise les nombres imaginaires en nombres complexes[note 8], qualificatif qui est encore en vigueur actuellement. Il pense ainsi avoir levé l'aura de mystère qui entourait ces nombres et qui était due en partie au vocabulaire choisi[note 9]. Cet avis est partagé par ses contemporains : « vous avez rendu possible l'impossible » est la phrase du discours adressé à Gauss en 1849, lors du cinquantenaire de son doctorat au Collegium Carolinum de Brunswick[52]. C'est également dans cet écrit de 1831 qu'il développe sa théorie sur les entiers de Gauss. On lui doit en outre la notion de norme qui, pour lui, correspond au carré du module : N(a+ib) = a²+b², la propriété : N(zz’) = N(z)N(z’) et la dénomination de complexe conjugué[53]. Mais l'exigence de rigueur de Gauss ne se satisfait pas d'une justification purement géométrique des complexes et il remet à plus tard une justification plus objective de i[54]. De nombreux mathématiciens reprennent ses travaux et contribuent à populariser la vision géométrique des complexes[55].

Hamilton et l'algèbre des couples de réels

William Rowan Hamilton, père des quaternions, traite les complexes comme des couples de réels munis d’une multiplication particulière (1833).

En Irlande, William Rowan Hamilton entreprend, lui, une démarche purement algébrique. Il s'inscrit dans un mouvement de l'école algébrique anglaise, qui prône la mise en place d'une algèbre symbolique et dont les grands noms sont George Peacock, Duncan Farquharson Gregory, George Boole et Auguste De Morgan[56]. En 1833, il présente à l'Académie royale d'Irlande sa Theory of conjugates functions or algebraic couples, suivie deux ans plus tard d'une théorie plus générale sur l'algèbre, mais il travaillait sur cette notion depuis 1826[57]. Hamilton s'appuie sur une définition des réels comme des intervalles de temps[58]. Il présente alors une construction algébrique sur des couples de réels. Il définit l'addition comme l'addition terme à terme de chaque membre du couple :

${\displaystyle (a,b)+(a',b')=(a+a',b+b').}$

Il définit une multiplication externe par un réel[note 10] :

${\displaystyle \lambda (a,b)=(\lambda a,\lambda b).}$

Il identifie alors λ au couple (λ, 0) et cherche à construire une multiplication sur les couples qui soit distributive. Il démontre alors que

${\displaystyle (\alpha ,\beta )(a,b)=(\alpha a,\alpha b)+(0,\beta a)+(0,\beta )(0,b).}$

Il lui reste alors à définir le dernier terme, qui pour des raisons d'homogénéité doit être proportionnel à β et b

${\displaystyle (0,\beta )(0,b)=(k\beta b,l\beta b).}$

Il obtient alors pour le produit

${\displaystyle (\alpha ,\beta )(a,b)=(\alpha a+k\beta b,\alpha b+\beta a+l\beta b).}$

Si, de plus, tout élément non nul doit être inversible, une condition supplémentaire doit s'ajouter

${\displaystyle l^{2}+4k<0}$

nécessaire et suffisante pour que le déterminant du système d'inconnues (α, β)

${\displaystyle {\begin{cases}\alpha a+k\beta b=1\\\alpha b+\beta a+l\beta b=0\end{cases}}}$

soit non nul pour tout couple (a, b) différent du couple (0, 0).

Hamilton choisit alors les valeurs les plus simples réalisant ces conditions[59] : l = 0 et k = –1. En réalité ces valeurs sont surtout les seules qui permettent au produit d'être compatible avec la norme définie par N(a, b) = a²+b² et Hamilton vérifie très vite que, pour les valeurs choisies :

${\displaystyle N((\alpha ,\beta )(a,b))=N(\alpha ,\beta )N(a,b).}$

Selon Remmert, le choix de Hamilton est grandement influencé par le désir de cette compatibilité[60]. Hamilton appelle le couple (1, 0) l'unité principale et (0, 1) l'unité secondaire. Il démontre ensuite qu'il existe une détermination principale du logarithme, que cette détermination principale induit une détermination principale de la racine n-ième et donc une détermination principale de la racine carrée de –1 qui se trouve coïncider avec l'unité secondaire. Donc, selon Hamilton, il est tout à fait légitime de parler de la racine carrée de –1 et d'écrire le couple (a, b) sous la forme a + √–1 b.

Hamilton tente également de construire des opérations sur des triplets de réels avec un produit qui conserverait la norme, mais en vain. Cette impossibilité sera démontrée par Ferdinand Georg Frobenius en 1877. Mais il a plus de chance avec les quadruplets de réels : c'est la création en 1843 du corps des quaternions.

Cauchy et la nouvelle définition de i

Augustin Louis Cauchy présente les complexes comme des polynômes (1847).

Augustin Louis Cauchy reste méfiant concernant les nombres complexes qui ne sont, selon lui, que des expressions symboliques, « une combinaison de signes algébriques qui ne signifie rien en elle-même » mais qui permet d'« écrire sous forme abrégée des résultats assez compliqués en apparence »[61]. Par souci de rigueur, il veut établir l'existence des quantités imaginaires dans un corpus algébrique ne faisant pas appel à l'intuition qui entraîne les paradoxes qui ont agité le siècle précédent (racine carrée, logarithme). Il craint que l'appel à la représentation géométrique ne fasse qu'ajouter d'autres paradoxes et d'autres intuitions fausses[61]. Il ne se résout que très tard (1844) à accepter la représentation géométrique des complexes et continue à voir dans le signe √–1 un simple outil destiné à faciliter les calculs.

Il faut attendre son écrit de 1847, Mémoire sur une nouvelle théorie des imaginaires et sur les racines symboliques des équations et des équivalences[62], pour le voir accepter les complexes comme des quantités et pas seulement comme des expressions symboliques. Dans ce mémoire, il travaille sur les restes des polynômes dans la division par le polynôme X² + 1. Pour indiquer qu'il travaille seulement sur les restes et non les polynômes eux-mêmes, il substitue à la variable X la variable i. Le polynôme X² + 1 ayant un reste nul dans la division par X² + 1, il peut se permettre d'écrire i² + 1 = 0 en toute légitimité. La quantité indéterminée i sera appelée par lui une racine symbolique du polynôme X² + 1. Le fait de considérer i comme la variable d'un polynôme lui permet d'écrire l'équivalence

${\displaystyle a+b~\mathrm {i} =c+d~\mathrm {i} \Leftrightarrow a=c{\text{ et }}b=d.}$

Il reconstitue alors toutes les opérations connues sur les complexes à l'aide de l'algèbre des polynômes. C'est la première esquisse d'une théorie sur les extensions algébriques de corps, qui mène à la définition de Bourbaki[63] du corps des complexes comme l'anneau des polynômes à coefficients dans ${\displaystyle \scriptstyle \mathbb {R} }$ quotienté par le polynôme X² + 1.

Quelques mois plus tard, dans son Mémoire sur les quantités géométriques, il reconnaît pleinement l'aspect géométrique des complexes. C'est lui qui baptise l'angle polaire de rayon OA argument de la quantité géométrique correspondante[64]. C'est également lui qui nomme affixe du point A le complexe a + i b si (a, b) sont les coordonnées de A[65].

La prudence et les réticences de Cauchy ne l'empêchent cependant pas de travailler durant toute la première moitié du XIX^e siècle à développer la théorie des fonctions de la variable complexe[66] ainsi que la théorie des résidus[67].

Complexe comme matrice de similitude

Plus tardivement apparaît une nouvelle présentation des nombres complexes comme matrices de similitudes directes planes. Cette présentation est inspirée par les idées de Wessel et Argand qui voient dans une multiplication d'un complexe par un autre une rotation suivie d'une homothétie. Une telle présentation apparaît en 1935 dans le livre d'Edward Thomas Copson, An introduction to the theory of functions of a complex variable[29]. C'est également le choix fait par les programmes de mathématiques de l'enseignement français de 1971[68]. Cette présentation évite de faire allusion à une quelconque extension du corps des réels, et d'introduire une multiplication sur les couples de réels qui semble arbitrairement créée. Elle s'appuie sur un savoir des élèves concernant les matrices carrées et les similitudes vectorielles directes planes. On démontre que l'ensemble des matrices de la forme

${\displaystyle {\begin{pmatrix}a&-b\\b&a\end{pmatrix}}}$

où a et b sont des réels quelconques, muni de l'addition et de la multiplication usuelle sur les matrices, est un corps commutatif. Les identifications

${\displaystyle {\begin{pmatrix}1&0\\0&1\end{pmatrix}}=1{\text{ et }}{\begin{pmatrix}0&-1\\1&0\end{pmatrix}}=\mathrm {i} }$

permettent l'écriture du complexe sous la forme a+ib avec la remarque i² = –1.

Dès le milieu du XIX^e siècle, les complexes ont définitivement intégré le corpus des mathématiques rigoureuses. Leur utilité indéniable a contribué à leur survie tant dans le domaine mathématique que dans le domaine physique.

Usages en mathématiques

Exemple de fractale : un ensemble de Julia (XX^e siècle)

Les nombres complexes se révèlent très tôt utiles dans la résolution des équations polynomiales, ainsi que l'expose Bombelli dès 1572. Ils permettent également aux mathématiciens de s'intéresser dès 1608 au théorème fondamental de l'algèbre. Ils sont utilisés dès le début du XVIII^e siècle dans le calcul intégral. Leur interprétation géométrique permet de démontrer plus simplement de nombreuses identités trigonométriques[69] et de nombreux théorèmes de géométrie plane comme le théorème de Ptolémée[70], le théorème de Cotes et la résolution d'un polygone[71], la droite de Wallace[72] ou le théorème de Napoléon.

Ils permettent un développement du calcul sur les intégrales elliptiques dès 1827[73]. Dans l’œuvre de Cauchy, père de l'analyse complexe et de la théorie des résidus, dès 1821, c'est un instrument de calcul qui permet de « rendre plus simples et plus concises, non seulement les formules analytiques, mais encore les méthodes à l'aide desquelles on parvient à les établir »[74]. Ils sont également à l’œuvre dans les équations algébriques, dans la démonstration du théorème d'Abel et dans la théorie de Galois.

Bernhard Riemann en fait une partie intégrante de son cours en 1851 et les utilise pour développer les surfaces de Riemann et la fonction zêta de Riemann. Au XX^e siècle, ils interviennent dans des domaines aussi variés que les fractales ou les courbes elliptiques.

Représentations en physique

Augustin Fresnel fait usage des nombres complexes en optique (1823).

Mais l'utilisation des nombres complexes dépasse également le champ des mathématiques pour servir de représentations de phénomènes physiques et d'outil unificateur. Dès 1823, Augustin Fresnel, dans son Mémoire sur la loi de modification que la réflexion imprime à la lumière polarisée[75], remarque que dans la loi de Snell-Descartes donnant l'angle de rayon réfracté en fonction de l'angle du rayon incident

${\displaystyle n_{1}\cdot \sin(\theta _{1})=n_{2}\cdot \sin(\theta _{2}),}$

lorsque n₁ > n₂, pour certaines valeurs de θ₁, la valeur de sin(θ₂) est plus grande que 1. Il obtient alors pour ${\textstyle \cos \theta _{2}={\sqrt {1-\sin ^{2}\theta _{2}}}}$ une valeur imaginaire[76] dont il réussit à interpréter le sens, unifiant ainsi en une seule formule ce qui se présentait jusqu'alors sous deux formes[77].

En 1860, c'est à l'aide des quaternions que James Clerk Maxwell écrit ses premières équations[78]. En 1893, Arthur Edwin Kennelly remarque que l'on peut généraliser la loi d'Ohm au courant alternatif en utilisant les complexes[79] et Charles Proteus Steinmetz fait l'inventaire de l'usage des complexes en électricité[80]. Les complexes apparaissent également dans les séries de Fourier et dans la résolution des équations différentielles linéaires.

---